29.4 (7.2.4). Решето числового поля для дискретного логарифмування

У п.9.2.5 розглянуто особливості факторизації з використанням загального решета числового поля. Аналогічно і для дискретного логарифмування в скінченному полі Галуа розроблено та застосовується решето числового поля (NFS). Як буде показано нижче, воно є найбільш ефективним щодо мінімальної складності дискретного логарифмування в скінченному полі Галуа. Розглянемо сутність основних етапів застосування решета числового поля при вирішенні задач дискретного логарифмування, яке зводиться до виконання таких етапів [426, 427]. При цьому як основоположну візьмемо роботу [427].

1. Спочатку обирається два багаточлени невеликого степеня f₁(x) та f₂(x), що є незвідними в Z[x] з малими коефіцієнтами, але такі, що f₁(x) та f₂(x), мають спільний корінь m у полі F(Р). Ці багаточлени визначають два числових поля Q (a₁) та Q (a₂). Оскільки m – корінь, то існує гомоморфізм φ_j кільця Z [a_j] для поля F(Р) (j ={1, 2}), але такий, що φ_j(a_j) = m. Далі розширимо φ_j до поля Q (a_j), не звертаючи уваги на потенційні проблеми існування подільності.

2. Кільце цілих чисел, не обов’язково буде унікальною фактор-базою, але кільце отриманих після ділення ідеалів буде завжди.

3. Для побудування решета NFS формуються дві фактор бази з ідеалів B₁ та B₂ (відповідно Q (a₁) та Q (a₂)), що складаються з простих гладких ідеалів. При цьому поняття гладкості визначається таким чином: отриманий після ділення ідеал I з Q (a_j) є гладким, якщо він може бути розкладений за фактор-базою B_j, та алгебраїчне число x є гладким, якщо отриманий після ділення ідеал áxñ вибрано з гладкого діапазону.

4. Етап просіювання здійснюється в такій послідовності. Спочатку знаходимо велику кількість пар малих цілих чисел (a_i, b_i), але таких, що – гладкі, тобто результат факторизації відомий.

5. Розглядаються числа поля Q (a₁) для лінійної алгебри за модулем р -1, а потім виробляється багато цілочисленних векторів (е_i) – таких, що отриманий після ділення ідеал

є (р-1)-го степеня. Але це не обов’язково виконується, тобто не означає, що алгебраїчне число є (р -1)- го степеня в Q (a₁). Однак, з використанням конкретних лінійних відображень з Q (a₁) у Z(p-1) Schirokauer (Широкаєру) [428] вдалося додати декілька лінійних рівнянь для того, щоб

було (р -1)-им степенем в Q (a₁).

Виходячи з цього, маємо, що

Отже,

Далі, логарифмуючи (9.58), отримаємо, що

З іншого боку, кожне 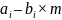має бути гладким, бо є гладким. Тому попереднє рівняння може бути подане у вигляді:

де В – набір невеликих простих чисел, і кожне – відоме ціле число. Для розв’язання задачі дискретного логарифмування потрібно отримати велику кількість таких лінійних рівнянь, а ще більше – для поля Q (a₂).

6. Коли рівнянь буде достатньо, можна буде розв’язати задачу дискретного логарифмування таким чином.

Для обчислення дискретного логарифма b = а^х mod р достатньо знайти експоненту е_i Z – таку, що

,

де кожне p_i – «добре» просте число, а не тільки p_i B, оскільки тільки для «добрих» простих чисел відомі логарифми.

7. Є кілька способів, щоб знайти такі показники. Наприклад, при використанні двовимірної решітки скорочення можна обчислити два лінійно незалежних цілочисленних вектори (A₁, B₁) і (A₂, B₂) з координатами , такі як

Звідси випливає, що для будь-яких цілих чисел a а також b:

Тепер, оскільки A_i та B_i достатньо малі, то можна, використовуючи техніку просіювання, спробувати знайти пару (a,b), але таку, що є гладкими при «добрих» простих числах. Якщо жоден кандидат не знайдено протягом розумного періоду часу, то спроби потрібно повторити, наприклад, замінити b на b_si, де s є найбільшим «добрим» числом.

Оцінка складності дискретного логарифмування за умови застосування решета числового поля наводиться нижче, у підрозділі 9.3.4.