98. Диаграмма усталостной прочности (диаграмма Хейга).

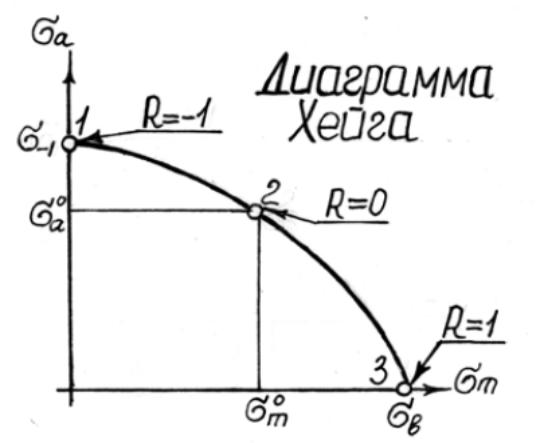
Диаграмма Хейга строится в координатах: среднее напряжение цикла σm – амплитуда цикла σa. При этом для ее построения необходимо провести усталостные испытания так же, как минимум, для трех режимов: 1 – симметричный цикл нагружения

2 – отнулевой цикл

3 – статическое растяжение

Соединяя экспериментальные точки (1, 2, 3) плавной кривой, получим график, характеризующий зависимость между значениями предельных амплитуд и значениями предельных средних напряжений в цикле.

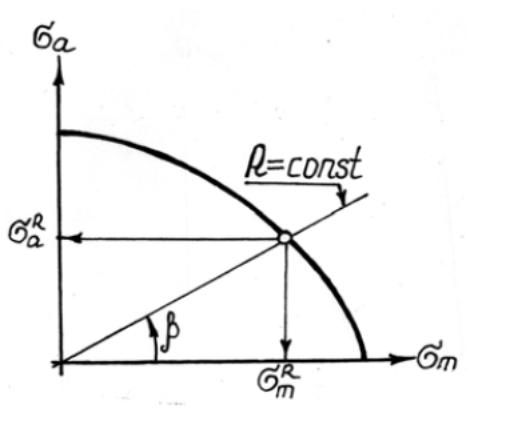
Здесь также можем провести луч, характеризующий циклы с одинаковой асимметрией:

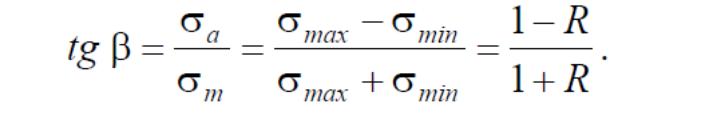
Тогда, для определения предела выносливости при заданной асимметрии цикла R нужно по приведенной формуле вычислить величину угла β и провести луч под этим углом до пересечения с линией 1-2-3, ордината точки пересечения даст нам величину предельной амплитуды σa и значение предельного среднего напряжения σm в цикле. Предел выносливости σR найдем в виде

99. Расчет на прочность при переменных напряжениях и линейном напряженном состоянии.

Расчет элементов конструкций, находящихся под действием переменных нагрузок, обычно начинают со статического расчета, целью которого является предварительное определение основных параметров. После разработки конструкции элемента проводят проверочный расчет его на выносливость, в результате которого определяют действительный (фактический) коэффициент запаса усталостной прочности  , который представляет собой отношение предела выносливости при симметричном цикле к действительным напряжениям детали, приведенным к этому циклу. Например, при изгибе

 

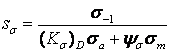.                                   (2.90)

 

Аналогично при кручении

 

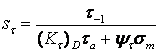,                                   (2.91)

 

где   и   –  коэффициенты снижения предела выносливости детали по сравнению с пределом выносливости образца:

 

 и  .       (2.92)

При совместном действии изгиба и кручении

 

.    

Примером линейного напряженного состояния может служить осевое растяжение-сжатие.

Рассмотрим задачу определения напряжений в площадке общего положения. Угол наклона этой площадки α будем отмерять от направления   до нормали к площадке  . Примем, что положительный угол α откладывается против хода часовой стрелки, а отрицательный по ходу часовой стрелки. Направим ось х вдоль нормали  , ось у – перпендикулярно ей

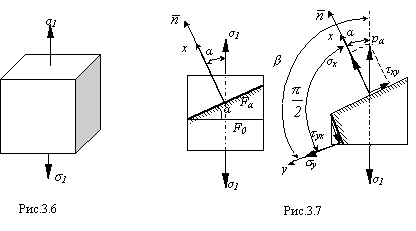Для определения напряжений s x и t ху  рассмотрим рис.3.7.

Получим:

где   - площадь наклонной площадки,

 - площадь поперечного сечения,

 - полное напряжение, действующее по наклонной площадке.

Учитывая, что  , получим:

.

Раскладывая pa на направление оси х и оси у, получим

,

Рассмотрим площадку b перпендикулярную площадке a, угол

. Направим ось y по нормали к этой площадке. Нормальные напряжения, действующие по этой площадке равны

.

Складывая sх и sу , получим

sx + sy = s1 = const,

т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам величина постоянная и равна главному напряжению.

Касательные напряжения, действующие по наклонной площадке b

,

т.е. справедлив закон парности касательных напряжений.

Нормальные напряжения sx по наклонной площадке a достигают максимального значения   при a = 0, т.е. в поперечном сечении.

Касательные напряжения τxy по наклонной площадке a достигают максимального значения   при a = ± 450.