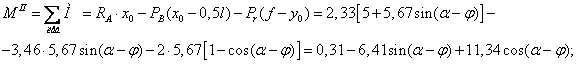Как
правило, основная проблема при
расчете сжатых стержней состоит в
том, чтобы сжимающие напряжения s
не
превышали бы критических значений
по устойчивости sКР , т.е.
 .
(7.17)
.
(7.17)
При
продольном изгибе центрально сжатый
стержень теряет несущую способность,
когда напряжения в его поперечных
сечениях достигают критических
значений. Поэтому необходимо ввести
в расчет коэффициент запаса
устойчивости n по отношению
к критическим напряжениям, с помощью
которого и определяется допускаемое
напряжение при расчете на устойчивость:
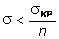 .
.
При
расчете же стержней на растяжение
применяют условие s < R,
гдеR - расчетное сопротивление
на растяжение.
Для
унификации расчетов на растяжение
и сжатие введем соотношение правых
частей двух последних неравенств:
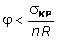 ,
(7.18)
,
(7.18)
откуда 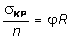 .
И тогда (7.17) можно записать так: s < jR.
.
И тогда (7.17) можно записать так: s < jR.
Величина j носит
название коэффициента уменьшения
расчетного сопротивления при
расчете на сжатие и является
функцией от гибкости стержня l(табл.
5).
Таким
образом, окончательно формула для
расчета стержней на устойчивость
принимает следующий вид:
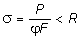 .
(7.19)
.
(7.19)
Несмотря
на простоту выражения (7.19) расчет
сжатых стержней производится,
как правило, в несколько этапов. Это
связано с тем, что величина j зависит
от формы и размеров сечения, поэтому
не может быть назначена заранее. В
связи с этим, подбор сечения
осуществляют итеративно, постепенно
приближаясь к тому, чтобы разница
между напряжением сжатия s и
расчетным сопротивлением на
растяжение R не превышала бы
3-.5
87.
Выбор материала и рациональной формы
поперечных сечений сжатых стержней.
О
выборе материала и рациональных
форм поперечных сечений для сжатых
стержней
Для
стержней большой гибкости  ,
когда критические напряжения не
превышают предела пропорциональности
материала, модуль упругости
,
когда критические напряжения не
превышают предела пропорциональности
материала, модуль упругости 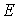 является
единственной механической
характеристикой, определяющей
сопротивляемость стержня потере
устойчивости. В этом случае
нецелесообразно применять сталь
повышенной прочности, так как
модули
для
различных сталей практически
одинаковы.
является
единственной механической
характеристикой, определяющей
сопротивляемость стержня потере
устойчивости. В этом случае
нецелесообразно применять сталь
повышенной прочности, так как
модули
для
различных сталей практически
одинаковы.
Для
стержней малой гибкости применение
специальных высокосортных сталей
целесообразно, так как в этом случае
повышение предела текучести стали
увеличивает критические
напряжения, а следовательно,
и запас устойчивости.
С
экономической точки зрения наиболее
рациональна такая форма поперечного
сечения стержня, при которой величина
наименьшего радиуса инерции 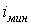 при
определенной площади является
наибольшей. Для удобства сравнения
различных сечений введем безразмерную
характеристику
при
определенной площади является
наибольшей. Для удобства сравнения
различных сечений введем безразмерную
характеристику
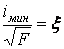 ,
,
которую можно
назвать удельным радиусом инерции.
значения 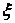 для
некоторых сечений:
для
некоторых сечений:
Сечение
|
|
Трубчатое
сечение 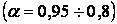
Трубчатое
сечение 
Уголок
Двутавр
Швеллер
Квадрат
Круг
Прямоугольник 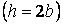
|
2,25-1,64
1,2-1,00
0,5-0,3
0,41-0,27
0,41-0,29
0,289
0,283
0,204
|
где 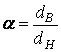 .
.
Анализ
данных показывает, что наиболее
рациональны трубчатые тонкостенные
сечения. Столь же рациональны и
коробчатые тонкостенные сечения.
Однако следует заметить, что при
проектировании тонкостенных трубчатых
и коробчатых сечений необходимо
предусматривать постановку диафрагм
(ребер жесткости) на определенных
расстояниях по длине стержня. Эти
диафрагмы препятствуют появлению
местных деформаций (короблений
стенок). Наименее рациональны сплошные
прямоугольные сечения.
При
расчете сжатых стержней на устойчивость
следует стремиться к тому, чтобы они
были равноустойчивыми во всех
направлениях. Для этого проектировать
сечения надо так, чтобы главные
моменты инерции были по возможности
одинаковыми. Трубчатые сечения
рациональны и с этой точки зрения.
Этому критерию удовлетворяют также
квадратные и круглые сечения.
Нерационально применять двутавровые
сечения и сечения в виде прямоугольника.
Однако если приведенные длины в
главных плоскостях различны, то и
главные моменты инерции также следует
проектировать разными, с тем чтобы
величины гибкостей стержня в обеих
главных плоскостях были одинаковыми
или хотя бы близкими между собой.
Если не удается сделать гибкости
одинаковыми, то расчет следует вести
по максимальной гибкости.
88.
Эпюры внутренних усилий плоских
кривых брусьев.
В
плоском криволинейном стержне так
же, как в плоской раме, состоящей из
прямолинейных стержней, возникает
три внутренних усилия: N, Q и М.
Процесс определения внутренних
усилий в криволинейном стержне тот
же, что и в раме. Особенность состоит
в новом правиле знаков для
изгибающего момента: изгибающий
момент считается положительным,
если он увеличивает кривизну стержня
(Если рассматриваемый стержень имеет
и прямолинейный, и криволинейный
участки, то для того, чтобы не было
противоречия из-за разного правила
знаков для изгибающего момента в
прямолинейной и криволинейной частях
стержня, принято строить эпюру
изгибающего момента со стороны
растянутых волокон без определения
знака). Правила знаков для продольной
и поперечной сил те же, что и при их
определении в плоских рамах.
Построение
эпюр внутренних усилий рассмотрим
на конкретном примере плоской
круговой балки (т. е. балки с осью,
очерченной по дуге окружности),
изображенной на рис. 3, а.
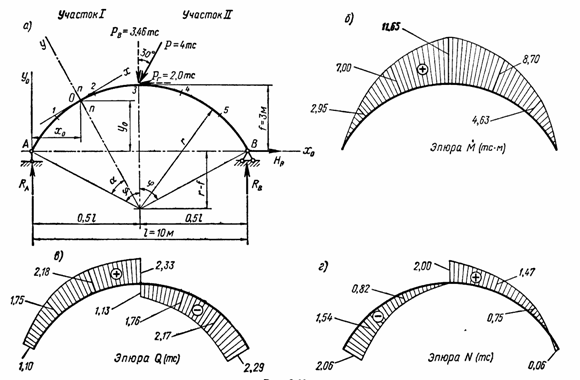
Рис.
3
Для
определения опорных реакций составим
уравнения равновесия:
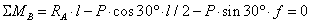 ,
,
откуда
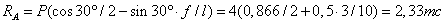 ;
;
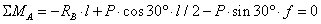 ,
,
откуда
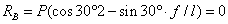 ;
;
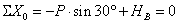 ,
,
откуда
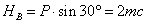
В
этих выражениях величины 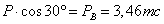 и
и 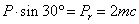 представляют
собой соответственно вертикальную
и горизонтальную составляющие
силы Р; ось
представляют
собой соответственно вертикальную
и горизонтальную составляющие
силы Р; ось 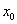 горизонтальна.
горизонтальна.
Определяем
значение радиуса r оси балки и
центрального угла  . Из рис.
3, а:
. Из рис.
3, а:
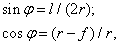
следовательно,
 ,
,
откуда
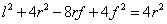
и

и 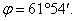
Проведем
через произвольную точку О участка
1 балки поперечное сечение n-n. Положение
этого сечения определяется
углом 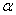 (рис.3, а). С
сечением n-n совместим
ось у подвижной системы
координат; ось хперпендикулярна
ей и касательна к оси балки в точке О.
Координаты точки О в неподвижной
системе координат х0у0 равны:
(рис.3, а). С
сечением n-n совместим
ось у подвижной системы
координат; ось хперпендикулярна
ей и касательна к оси балки в точке О.
Координаты точки О в неподвижной
системе координат х0у0 равны:
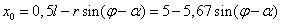 ;
;
 .
.
Составим
выражения изгибающего момента  ,
поперечной силы
,
поперечной силы 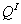 и
продольной силы
и
продольной силы 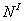 в
поперечных сечениях участка I
балки:
в
поперечных сечениях участка I
балки:
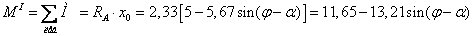 ;
;
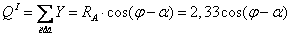 ;
;
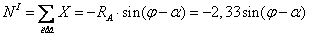 .
.
Аналогично
составим выражения 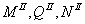 для
участка II балки:
для
участка II балки:
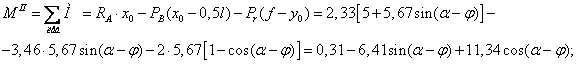
 ;
;
 .
.
По
полученным значениям усилий в
поперечных сечениях балки на рис.
3, б, в, г построены эпюры М, Q и N.
Связь
между усилиями М, Q и N, действующими
в поперечных сечениях кривого
бруса, определяется следующими
дифференциальными зависимостями:
 ; (1)
; (1)
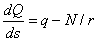 ; (2)
; (2)
 . (3)
. (3)
где q и t —
интенсивности распределенных
нагрузок соответственно перпендикулярной
и параллельной оси бруса; ds -
длина элементарного отрезка оси
кривого бруса.
Формула
(1) аналогична формуле Журавского
для прямых брусьев.
Зависимости
(1) - (3) могут использоваться для
проверки построенных эпюр М, Q и N. Проверим
с их помощью эпюры, изображенные на
рис. 3.
На
участке I балки (см. рис. 3, а)
ординаты эпюры Q положительны,
а на участке II — отрицательны.
Поэтому в соответствии с
зависимостями (1) и (3)
значения М и N на участке I возрастают
слева направо (т.е. с увеличением
криволинейной координаты s), а на
участке II — убывают. Ординаты
эпюры N на участке I отрицательны,
а на участке II — положительны;
в соответствии с зависимостью
(2) значения Q на участке I возрастают,
а на участке II — убывают.
Производная 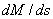 на
отрезке, например, 2-3 оси балки
(см. рис. 3, а) имеет среднее значение,
равное (см. рис.3, 6)
на
отрезке, например, 2-3 оси балки
(см. рис. 3, а) имеет среднее значение,
равное (см. рис.3, 6)
 ,
,
где
длина участка
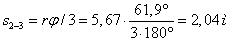 .
.
Этому
среднему значению производной в
соответствии с зависимостью (1)
примерно равна средняя величина Q на
отрезке 2-3 (см. рис. 3, в).
Производная 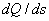 на
участке, например, 3-4 балки
имеет среднее значение
на
участке, например, 3-4 балки
имеет среднее значение
 .
.
В
соответствии с зависимостью
(2) такое же примерно значение на
отрезке 3-4 имеет среднее отношение 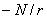 ,
равное
,
равное
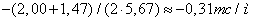 .
.
Аналогично
можно проверить выполнение условий
(1)-(3) и на других отрезках оси балки.
89.
Определение напряжений в поперечных
сечениях бруса большой кривизны при
чистом изгибе. Эпюра напряжений.
Выведем
формулы для определения нормальных
напряжений в брусьях большой кривизны.
При
выводе этих формул предполагается,
что:
1)
кривой брус является плоским (т.е.
ось его представляет собой плоскую
кривую);
2)
брус симметричен относительно
плоскости, в которой расположена
его ось, а внешние силы действуют в
этой плоскости;
3)
поперечные сечения бруса, плоские
до его деформации, остаются плоскими
и после деформации (гипотеза плоских
сечений);
4)
давление продольных волокон бруса
друг на друга не влияет существенно
на распределение напряжений в брусе,
а потому его можно не учитывать.
При
изгибе брусьев малой кривизны
нормальные напряжения с достаточной
степенью точности можно
определять по формуле Навье для
балок с прямой осью. Максимальные
напряжения, подсчитанные по
формуле Навье для бруса
прямоугольного сечения с отношением 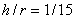 ,
отличаются на 2%
от напряжений, вычисленных по
формулам для бруса большой кривизны;
при
,
отличаются на 2%
от напряжений, вычисленных по
формулам для бруса большой кривизны;
при 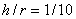 -
на 3,5%, при
-
на 3,5%, при  -
на 7%.
-
на 7%.

|


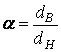 .
.