Дұрыс пішінді дененің тығыздығын өлшеу

1. Микрометрді және штангенциркульді қолдану әдістерімен танысу.

2. Штангенциркульмен берілген қатты дененің қалыңдығын x_i ұзындығы y_i мен енін z_i 10 рет өлшеу керек.

3. Дененің m массасын анықтаңыз.

4. Стьюдент коэфициентін t_{р, n-1} кестесі бойынша өлшеу сандары (n-1) мен берілген сенім ықтималы Р үшін табу керек.

№ п/п	уi, мм	<у>, мм	Dуi, мм	(Dуi)2	S<у>	Ру	tp, n-1	eу	qу, мм	Dу, мм
1 2 3 4 5 6 7 8 9 10
№ п/п	zi, мм	<z>, мм	Dzi, мм	(Dzi)2	S<z>	Рz	tp, n-1	ez	qz, мм	Dz, мм
1 2 3 4 5 6 7 8 9 10
№ п/п	xi, мм	<x>, мм	Dxi, мм	(Dxi)2	S<x>	Рх	tp, n-1	ex	qx, мм	Dх, мм
1 2 3 4 5 6 7 8 9 10

5. Берілген сенім ықтималы Р арқылы тура өлшеудің нәтижелерінің сенім аралықтарын есептеу керек.

6. Орташа мәндері бойынша, заттың тығыздығын <> есептеңіз және зат дайындалған материалдың тығыздығын анықтамалық кестеден табыңыз.

7. Салыстармалық қателік пен сенім аралығын анықтаңыз.

8. 8.Өлшеудің соңғы нәтижесін жазыңыз.

№ 2 зертханалық жұмыс.

Математикалық маятниктің көмегімен еркін түсу үдеуін анықтау.

Жұмыстың мақсаты: Математикалық маятник арқылы теңселгіш қозғалысты және еркін түсу үдеуін анықтау.

Теориялық кіріспе.

Бір-бірінен r қашықтықта орналасқан массалары m1 және m2 материалық нүктенің Ньютонның бүкіләлемдік заңы бойынша бір-біріне әсер етеді:

F G [1]

G 6,672 10−11H м2 / кг- Гравитациялық тұрақтылық.

[1] формуладағы тартылыс заңына сәйкес оны дненің жерге тартылу күшін есптегенде де қолдануға болады, яғни:

[2]

M₃ және R₃- масса және Жердің радиусы, h – Жер мен дененің ара қашықтығы, g – еркін түсу үдеуі.

Ал, [2] формула бойынша Жерге еркін түсу үдеуі мынаған тең:

[3]

және жердің центріне тік бағытталған.

Жердің бетінен (h=0) есептегенде еркін түсу үдеуінің шамасы g=9,8м/с². Жердің жалпақтығы (R₃  const) және оның айналуы Жерге еркін түсу үдеуінің шамасын өзгертеді,яғни, экваторда (g ≈9,78 м/с²) , ал, полюсте (g ≈9,83 м/с²). Сонымен қатар, Жердің айналуы еркін түсу үдеуінің жергілікті жердің биіктігіне тәуелділігіне әкеліп соғады.

Математикалық маятник деп –құрылғыдағы созылмайтын салмақсыз жіпке ілінген және вертикаль жазықтықта ауырлық күшінің әсерінен тербеле алатын пішімі кіші денелерді (материялық нүкте) айтамыз. (1-сурет)

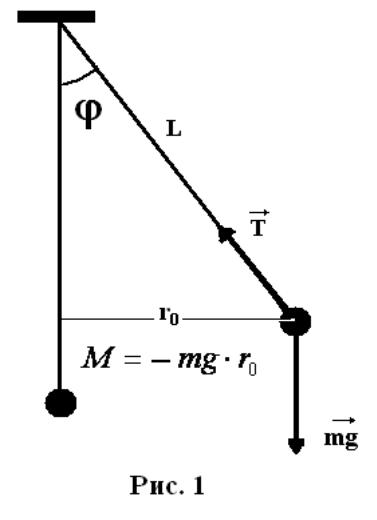
Тербелмелі қозғалыс динамикасының негізгі заңы (Ньютонның екінші заңы бойынша) дене және оның бұрыштық үдеуіне  әсер ететін қорытқы М момент күшімен байланысты.

немесе J M [4]

J – айналу осіне қатысты дененің инерция моменті.

Жіптің созылуының күш моменті Т маятниктің айналу осіне қатысты нөлге тең, сондықтан да қорытқы момент ауырлық күш моментіне тең:

[5]

Мұндағы, - ауырлық күш иіні. [5] формуладағы «-» таңбасы айналу моментінің бағыты мен маятниктің ауытқу бұрышы қарама-қарсы екенін білдіреді.

[4] және [5] формуланы пайдалана отырып және айналу осіне қатысты материялық нүктенің инерция моменті тең: , ал оның бұрыштық жылдамдығы '' , яғни, '' – жіптің вертикальдан ауытқу бұрышы бойынша уақыттың екінші ретті туындысы, онда:

[6]

Маятниктан ауытқу бұрышы аз шама болса, яғни, sin онда маятник қозғалысының дифференциалдық теңдеуі мынаған тең:

= 0 [7]

М ұндағы =g/L – маятниктің ауытқу жиілігі. Берілген теңдіктің шешімі:

[8]

мұндағы, - ауытқу амплитудасы, - ауытқудың бастапқы фазасы. Осындай амплитуда аз шамада маятник мынадай жиілікте және периоды . Яғни,

[9]

Қондырғаны орналастыру және формулалар.

Орналастыру схемасы 3-суретте көрсетілген. Кронштейндегі (2) екі жұқа жіпке ілінген Математикалық маятникқа металл шар (1) қолданылады, осы кронштейнде маятниктің ұзындығын өзгертетін ролик (3) орналасқан. Кронштейннің төменгі жағында фотоқұрылғы (4) бекітілген, кронштейннің ара-қашықтығы қондырылған штатив шкала (5) арқылы анықталады.

Еркін түсу үдеуін экспериментті анықтау үшін [9] формуланы мына түрде жазып аламыз:

[10]

мұндағы, - периодтың квадраты мен маятник ұзындығы арасындағы пропорционал коэффициент.

Маятниктің L ұзындығын өзгерту және оның тербеліс периодын анықтау арқылы нүктелер қатарын табамыз (L_i ,T_i). T² тербеліс периодын вертикаль ось бойынша калдыра отырып нүктелерді T² f (L) графикте саламыз, ал горизонталь ось бойынша маятниктің сәйкесінше L ұзындығын. Тік сызық параметрлерінің графикалық сипаттамаларының анықтамасына сәйкес «Өлшемдердің шешімдерінің графикалық өңдеулері» бөлімінің кіріспесінде келтірілгендей ең жақсы түзу өткіземіз. T² f (L) функциясының графигінен тангенс бұрышының көлбеуін анықтаймыз және g_э еркін түсу үдеуінің эксперименттік мағынасын анықтаймыз:

g_э= [11]

g_э мағынасынан алынған интервал сенімділігін жанама өлшеудің қателіктері арқылы байқауға болады:

 g_э

- Стьюдент коэффициенті, яғни, интервал сенімділігінің таңдауына р және өлшем санына п байланысты.

Нәтижесін мына түрде жазамыз: р= ;

Жұмыстың орындалу барысы

Керекті құрал-жабдықтар: Математикалық маятник фотоқұрылғыдағы тіреуіш, секундомер.

Маятник қозғалыс кезінде фотоэлементтерге тиіп кетпес үшін және фотоқұрылғы жұмыс үстелінің центрі арқылы өтуі үшін тіреуішті тік орналастыру керек.

1. Вертикаль тіреуіштегі шкала бойынша маятниктің L₁ ұзындығын табу.

2. Маятникті тепе-теңдік күйінен (5 – 6)⁰ қисайтып, одан кейін «Сброс» кнопкасын басу. Таймердің көрсетуі бойынша N= 50-40 тербеліс санына кеткен уақытты белгілеп, кестеге жазып қою.

3. Маятниктің тербеліс периодын мына формула бойынша табу: T t / N

4. Математикалық маятниктің ұзындығын өзгерту арқылы [1] және [3] пунктті кемінде 5рет қайталау.

5. Берілген кестеден T² f (L) графигін тұрғызу. Графикті пайдаланып [11] формула арқылы g_эеркін түсу үдеуін анықтау. [12] формула арқылы сенімділік интервалын бағалау және жазып қою.

6. Қателіктің экспериментальды және стандартты мағынасын мына формула арқылы есептеп , кестенің соңғы бағанына жазып қою.

Нәтиже кестесі

№	L, мм	t, c	N	T, c
1
2
3
4
5
g g g м/c2	; p=

Қорытынды сұрақтар:

1. Бүкіләлемдік тартылыс заңы?

2. Дененің тартылс күші және еркін түсу үдеуі?

3. Математикалық маятник дегеніміз не?

4. Математикалық маятниктің тербеліс жиілігі және периоды?

5. Математикалық маятник арқылы еркін түсу үдеуін қалай анықтауға болады?

№3 Зертханалық жұмыс