Занятие №4. Тема: Повторные независимые испытания. Схема Бернулли. Теоремы Пуассона, Лапласа.

Основные формулы:

1. Формула Бернулли: .

2. Локальная теорема Лапласа: , где .

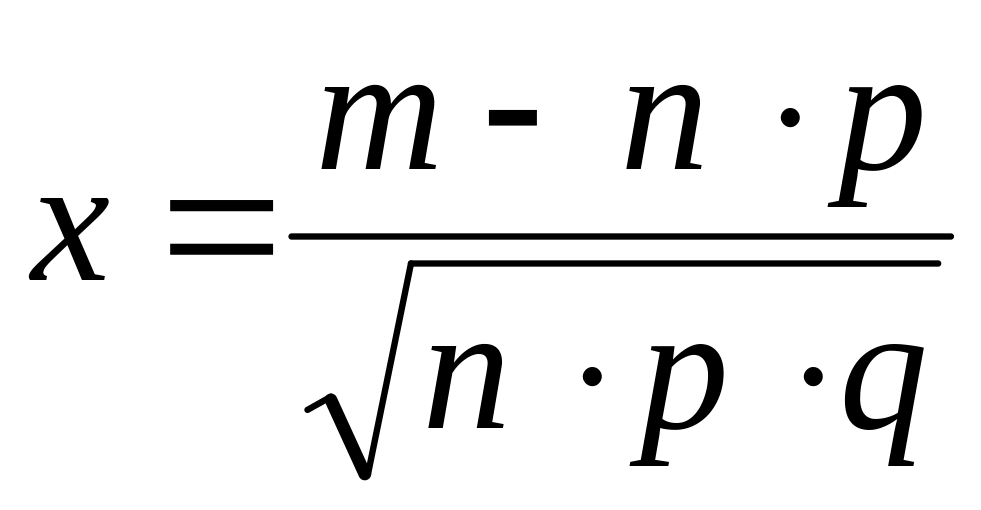При считают, что . Если , то .

3. Интегральная теорема Лапласа: , где

.

При считают, что . Если , то .

1. Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из 5 посеянных семян взойдут: а) четыре; б) не менее четырех.

2. Статистикой установлено, что из каждой 1000 родившихся детей в среднем рождается 485 девочек и 515 мальчиков. В семье 5 детей. Найти вероятность того, что среди этих детей: а) три девочки; б) не более трех девочек; в) не менее двух, но не более четырех девочек.

3. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз; б) не менее двух раз.

4. Найти вероятность того, что событие А появиться не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.

5. Вероятность появления события А в каждом из 625 испытаний равна 0,64. Найти вероятность того, что событие А в этих испытаниях появиться ровно 415 раз.

6. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

7. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.

8. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.

9. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах стрелок поразит мишень не менее 71 раза и не более 80 раз.

10. Вероятность появления события в каждом из 100 независимых испытаний, постоянна и равна 0,8. Найти вероятность того, что событие появиться: а) не менее 75 и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

11. Вероятность появления события в каждом из 2100 независимых испытаний, постоянна и равна 0,7. Найти вероятность того, что событие появиться: а) не менее 1470 и не более 150 раз; б) не менее 1470 раз; в) не более 1469 раз.

12. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появиться не менее 75 раз?

13. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован не правильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.

14. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено: а) ровно три изделия; б) менее трех изделий; в) более трех изделий; г) хотя бы одно изделие.

15. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных.

16. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно 2; б) менее двух; в) более двух; г) хотя бы одну.