Диапазон регулирования (отношение наибольшего передаточного числа к наименьшему) обычно 3—6, реже 10—12. Виды механических вариаторов

• Фрикционные вариаторы:

  • лобовые;

  • конусные;

  • шаровые;

  • многодисковые;

  • торовые;

  • волновые;

  • клиноременные.

• Вариаторы зацепления:

  • цепной вариатор.

  • высокомоментный вариатор

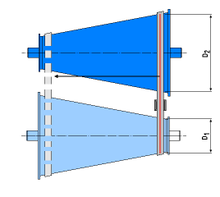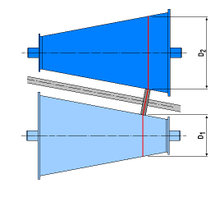Клиноремённый вариатор с клиновой цепью Фрикционный конусный вариатор с ремнем Фрикционный конусный вариатор с роликом. В настоящее время на автомобилях применяют два типа вариатора: клиноременной и торовый. Торовые вариаторы способны передавать больший крутящий момент, чем клиноременные. При этом им присущи недостатки клиноременных, так как усилие передается также за счет трения.

I=n1/n2-передаточное отношение. I=d2max/d1(1-E), E-коэффициент скольжения(0,02-0,05)

I1=d2max/d1; i2=d2min/d1; i1/i2=диапазон регулирования(D=d2max/d2min≤3-4)

23. Особенности работы цилиндрических косозубых, шевронных передач; расчет сил, действующих в косозубом зацеплении.

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение рис. 2.3.14.

; Рис. 2.3.1 Цилиндрическая а) косозубая б) и шевронная передача

С увеличением угла наклона линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются рис.2.3.15, но при этом увеличивается и осевая сила Fа, что нежелательно. Поэтому в косозубых передачах принимают угол .

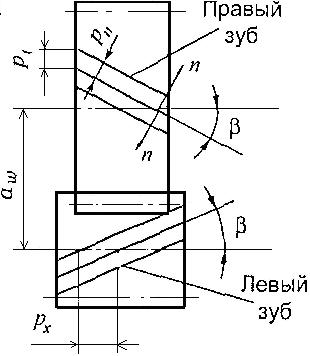Рисунок 2.3.15 Геометрия косозубых колес

Основные геометрические размеры зависят от модуля и числа зубьев. При расчёте косозубых колёс учитывают два шага: нормальный шаг зубьев pn - в нормальном сечении, окружной шаг pt – в торцовом сечении; при этом Соответственно шагам имеем два модуля зубьев:

(2.3.22) (2.3.23) при этом (2.3.24)

где mt и mn – окружной и нормальный модули зубьев. За расчётный принимают модуль mn, значение которого должно соответствовать стандартному. Это объясняется следующим: для нарезания косых зубьев используется тот же инструмент, что и для прямозубых, но с соответствующим поворотом инструмента относительно заготовки на угол . Поэтому профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба; следовательно, mn=m. Диаметры делительный и начальный

(2.3.25)

Диаметры вершин и впадин зубьев

(2.3.26) (2.3.27)

Межосевое расстояние

(2.3.28)

4.5.2 Эквивалентное колесо

Профиль косого колеса в нормальном сечении n-n (рис. 3) соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем прямозубого колеса. Расчет косозубых колес проводят через параметры эквивалентного прямозубого колеса. Нормальное к линии зуба сечение делительного цилиндра имеет форму эллипса. Радиус кривизны эллипса при зацеплении зубьев в полюсе профиль зуба в этом сечении достаточно близко совпадает с профилем приведённого прямозубого колеса, называемого эквивалентным,профиль зуба в этом сечении достаточно близко совпадает с профилем приведённого прямозубого колеса, называемого эквивалентным.

Делительный диаметр: (2.3.29) эквивалентное число зубьев: (2.3.30) или (2.3.31) где z – действительное число зубьев косозубого колеса. С увеличением возрастает возрастает . Это одна из причин повышения прочности косозубых передач.