6.2.1 Скорость скольжения в передаче. Передаточное число

Во время работы червячной передачи витки червяка скользят по зубьям червячного колеса рис. 2.5.11. Скорость скольжения направлена по касательной к винтовой линии делительного цилиндра червяка и определяется из параллелограмма скоростей

(2.5.11)

Как видно из формулы, всегда us > u1. Большое скольжение в червячной передаче повышает изнашиваемость зубьев червячного колеса, увеличивает склонность к заеданию. Передаточное число червячной передачи определяют по условию, что за каждый оборот червяка колесо поворачивается на число зубьев, равное числу витков червяка:

(2.5.11)

где и — угловые скорости червяка и колеса; z1 и z2 — число витков червяка и число зубьев колеса. На практике в силовых передачах применяют червяки с числом витков z1 = 1; 2; 4. С увеличением z1 возрастают технологические трудности изготовления передачи и увеличивается число зубьев червячного колеса z2. Число витков червяка z1 зависит от передаточного числа и.

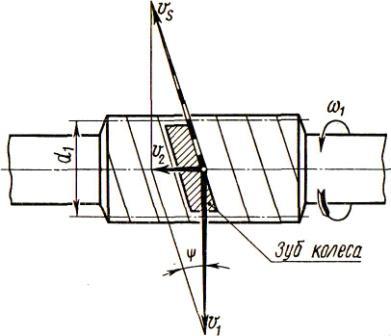Рисунок 2.5.11 схема определения скорости скольжения в червячной передаче

Во избежание подреза основания ножки зуба в процессе нарезания зубьев принимают z2?26. Оптимальным является z2 = = 40...60. Диапазон передаточных чисел в этих передачах u = 10...80.

6.2.2 Силы в зацеплении

В приработанной червячной передаче, как и в зубчатых передачах, сила червяка воспринимается не одним, а несколькими зубьями колеса. Для упрощения расчета силу взаимодействия червяка и колеса Fn принимают сосредоточенной и приложенной в полюсе зацепления П по нормали к рабочей поверхности витка. По правилу параллелепипеда Fn раскладывают по трем взаимно перпендикулярным направлениям на составляющие Ff1, Fr1, Fa1 рис. 2.5.12. Для ясности изображения сил, u червячное зацепление раздвинуто.

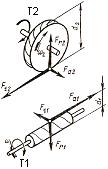Рисунок 2.5.12 Схема сил, действующих в червячном зацеплении

Окружная сила на червячном колесе численно равна осевой силе на червяке (2.5.13), где T2— вращающий момент на червячном колесе. Окружная сила на червяке численно равна осевой силе на червячном колесе : (2.5.14) (2.5.14), где T1— вращающий момент на червяке; — к.п.д. передачи. Радиальная сила на червяке численно равна радиальной силе на колесе (2.5.15). Направления осевых сил червяка и червячного колеса зависят от направления вращения червяка, а также от направления линии витка. Направление силы всегда совпадает с направлением вращения колеса, а сила направлена в сторону, противоположную вращению червяка.

33. Анализ напряженного состояния зуба зубчатого колеса при передаче нагрузки.

Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. В качестве исходной принимают формулу Герца для наибольших контактных напряжений при сжатии цилиндров, соприкасающихся по образующим (рис. 2),

где E - приведенный модуль упругости материалов зубчатых колес; μ — коэффициент Пуассона; ρ_пр — приведенный радиус кривизны профилей сцепляющихся зубьев в полюсе зацепления; q=F/l_k — нормальная нагрузка на единицу l_k контактной линии зуба; F — сила давления между сопряженными зубьями. Приведенный модуль упругости

где E₁ и E₂ - соответственно модули упругости материала шестерни и колеса. Если материалы шестерни и колеса одинаковы, то E=E₁=E₂. Приведенный радиус кривизны цилиндрической прямозубой передачи

где ρ₁ и ρ₂ — соответственно радиусы кривизны профилей зубьев шестерни и колеса; знак плюс для наружного, минус для внутреннего зацепления. где Z_H — коэффициент формы сопряженных поверхностей зубьев в полюсе зацепления:

Z_M — коэффициент, учитывающий механические свойства материалов сопряженных зубьев:

Таким образом, исходная расчетная формула для проверочного расчета зубьев цилиндрических передач на контактную прочность, как она дана в ГОСТ 21354-75, записывается в виде

де [σ_H] — допускаемое контактное напряжение для зубьев. Удельная расчетная окружная сила

где F_t — расчетная окружная сила передачи; K_Hα — коэффициент неравномерности распределения нагрузки между зубьями в косозубых передачах; K_Hβ — коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев; K_Hv - коэффициент динамической нагрузки, возникающей в зацеплении (см. табл.); b_w — рабочая ширина венца зубчатого колеса.

34. Планетарные передачи. Конструкции, особенности сборки и нагружения зубчатых колес. Основы расчета на прочность.

Планетарная передача (дифференциальная передача) — механическая система, состоящая из нескольких планетарных зубчатых колёс (шестерён), вращающихся вокруг центральной, солнечной, шестерни. Обычно планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую (коронную) шестерню, имеющую внутреннее зацепление с планетарными шестернями. Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение несколькими разными способами. Основными элементами планетарной передачи можно считать следующие:

• Солнечная шестерня: находится в центре;

• Водило: жёстко фиксирует друг относительно друга оси нескольких планетарных шестерён (сателлитов) одинакового размера, находящихся в зацеплении с солнечной шестерней;

• Кольцевая шестерня: внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями.

При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, другой элемент используется как ведущий, а третий — в качестве ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также того, какой элемент закреплён.

Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила.

КПД составляет 0,95...0,98 Силы в зацеплении.

dwa, dwg-диаметры соответствующих колёс

Ft-окружные силы в зацеплении (условно смещены)

Для обычных передач.

Ftab-окружная сила на ведущем колесе

Ftba-Ha ведомом, Fh=Ftga+Ftgb

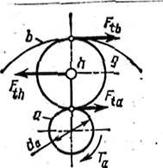
Два момента на ведущем и на ведомом звене всегда известны, т.е. Например:

В планетарных передачах условно принимается на ведущем+Т, а на ведомом -Т. Сила в зацеплении центральных колёс находится:

Ftag= ; Ftgb=

где n_w-число сателлитов;

-коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами.

Расчётное контактное напряжение в полюсе зацепления определяется по формуле:

ZHZEZ ;

и должно удовлетворять условию:

где Zh-коэффициент, учитывающий форму спряжённых поверхностей зубьев.

ZE-коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колёс.

Z -коэффициент, учитывающий суммарную длину контактных линий; U - передаточное число;

dwa- начальный диаметр шестерни. Удельная расчётная окружная сила:

W_Ht= KH KH KH ,

где расчётная окружная сила:

F_Ht=

где н-коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами;

nw-число сателлитов;

КH -коэффициент, учитывающий распределение нагрузки между зубьями;

КH -коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;

KH -коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении.

Расчётное напряжение изгиба зубьев:

F= ,

где YF-коэффициент, учитывающий форму зуба;

Y -коэффициент, учитывающий перекрытие зубьев.

35. Тепловой расчет редукторов; опасность перегрева, выбор типа смазки.

Тепловой расчет, охлаждение и смазка передачи Механическая энергия, потерянная в передаче, превращается в тепловую и нагревает передачу. Если отвод теплоты недостаточный, передача перегревается и выходит из строя. Количество теплоты, выделяющейся в передаче в секунду, или тепловая мощность,

 

 

где Рх—мощность на входном валу, Вт; η— КПД передачи. Через стенки корпуса редуктора теплота отдается окружа¬ющему воздуху, происходит естественное охлаждение. Коли¬чество теплоты, отданной при этом в секунду, или мощность теплоотдачи,

 

 

где А—площадь поверхности охлаждения, м2; tx—внутренняя температура редуктора или температура масла, °С; t0 — температура окружающей среды (воздуха), сС; К—коэф¬фициент теплоотдачи, Вт/(м2 °С). Под площадью поверхности охлаждения А понимают только гу часть площади наружной поверхности корпуса редуктора, которая изнутри омывается маслом или его брыз¬гами, а снаружи — свободно циркулирующим воздухом. По последнему признаку обычно не учитывают площадь по¬верхности днища корпуса. Если корпус снабжен охлаждаю¬щими ребрами, то учитывают только 50% площади их поверхности.