
- •Булевы функции от n переменных
- •Теорема 3.1.
- •Табличное представление
- •Булевы функции от 1-ой и 2-х переменных
- •Формулы
- •Определение 3.2.
- •Определение 3.3.
- •Булевы функции и логика высказываний
- •Сокращенные днф
- •Многочлены Жегалкина
- •2. Классификация firewall’ов. Пакетные фильтры, stateful inspection firewall’ы и прокси прикладного уровня.
- •Классификация firewall’ов
- •Установление тср-соединения
- •Пакетные фильтры
- •Пограничные роутеры
- •Пример набора правил пакетного фильтра
- •Персональные firewall’ы и персональные устройства firewall’а
- •Прокси-сервер прикладного уровня
- •Выделенные прокси-серверы
- •Гибридные технологии firewall’а
- •Трансляция сетевых адресов (nat)
- •Статическая трансляция сетевых адресов
- •Скрытая трансляция сетевых адресов
Булевы функции и логика высказываний
Как мы уже отметили, Дж. Буль ввел булевы функции для решения логических задач. В логике под высказыванием понимают некоторое повествовательное предложение, относительно которого можно сказать, истинно оно или ложно. Логика высказываний занимается выяснением истинности тех или иных высказываний, связью между истинностью различных высказываний и т.п.
Булевы функции могут служить полезным инструментом при решении многих логических задач.
Каждую переменную можно рассматривать как некоторое элементарное высказывание, принимающее одно из двух значений: 1 (истина) или 0 (ложь). Сложным высказываниям сооответствуют формулы, построенные из элементарных высказываний с помощью логических связок. Вычисляя значения задаваемых ими функций, можно устанавливать зависимости истинностных значений сложных высказываний от значений входящих в них элементарных высказываний. Рассмотрим следующий пример.
Пример 3.1.Пусть известно, что в дорожном проишествии участвовали три автомобиля с водителями A, B и C. Свидетели проишествия дали следующие показания:
1-ый свидетель: если A виновен, то из остальных B и C хоть один не виновен;
2-ой свидетель: если C не виновен, то виновен кто-то один из пары A, B но не оба вместе;
3-ий свидетель: в столкновении виновны не менее двух водителей.
Опишите показания свидетелей в виде булевых формул и постройте таблицу значений их конъюнкции. Можно ли на основании этих показаний сделать вывод, что C является виновником проишествия? Можно ли однозначно определить второго виновника?
Для ответа на эти вопросы введем три переменные, соответствующие следующим высказываниям: X1 : " виновен A ", X2 : " виновен B " и X3 : " виновен C ". Тогда показания 1-го свидетеля описываются формулой Φ1=(X1 (¬X2 ¬X3)) , показания 2-го свидетеля - Φ2= (¬ X3 (( X1 X2) ¬(X1 X2))), а 3-го свидетеля - Φ3= ((X1 X2)\vee ((X1 X3) ( X2 X3))) . Показаниям всех трех свидетелей соответствует конъюнкция этих формул Ψ= (Φ1 (Φ2 Φ3)) . Составим таблицы значений для функций fΦi (i=1,2,3) , а затем - для fΨ.
Таблица 3.5. Функция fΦ1 |
|
||||||||||||||||||||
X1 |
X2 |
X3 |
(X1 |
|
(¬ |
X2 |
|
¬ |
X3)) |
|
|||||||||||
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
|||||||||||
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
|||||||||||
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
|||||||||||
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|||||||||||
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
|||||||||||
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
|||||||||||
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
|||||||||||
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
|||||||||||
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|||||||||||
Таблица 3.6. Функция f Φ2 |
|||||||||||||||||||||
X1 |
X2 |
X3 |
(¬ |
X3 |
|
(( X1 |
|
X2) |
|
¬ |
(X1 |
|
X2))) |
||||||||
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
||||||||
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
||||||||
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
||||||||
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
||||||||
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
||||||||
\ 1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
||||||||
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.7. Функция f Φ3 |
|||||||||||||||||||
X1 |
X2 |
X3 |
((X1 |
|
X2) |
|
((X1 |
|
X3) |
|
( X2 |
|
X3))) |
||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
||||||
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
||||||
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
||||||
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
||||||
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
Таблица 3.8. Функция f Ψ |
|
|
|
|
|||||||||||||||
X1 |
X2 |
X3 |
(\Phi1 |
|
(\Phi2 |
|
\Phi3)) |
|
|
|
|
||||||||
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
||||||||
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
||||||||
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
||||||||
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
||||||||
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
||||||||
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
||||||||
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
|
||||||||
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из этой таблицы следует, что fΨ(X1,X2,X3)=1 на двух наборах: (X1=0, X2=1, X3=1) и (X1=1, X2=0, X3=1) (строки с этими наборами подчеркнуты). Поскольку в обоих случаях X3=1 , можно сделать вывод, что С является одним из виновников проишествия. Однозначно определить второго виновника полученная от свидетелей информация не позволяет, так как в одном случае им является А, а в другом - В.
Важную роль в логике играют понятия тождественно истинной и выполнимой формулы.
Определение
Булева формула Φ называется тождественно истинной, если она истинна при любых значениях входящих в нее переменных, т.е. функция fΦ тождественно равна 1.
Булева формула Φ называется выполнимой, если существует такой набор значений переменных, на котором она истинна, т.е. функция fΦ равна 1 хоть на одном наборе аргументов.
Как проверить тождественную истинность или выполнимость формулы Φ? На первый взгляд кажется, что ответ прост - построим по Φ таблицу для функции fΦ , и, если в столбце значений стоят только единицы, то заключаем, что Φ тождественно истинна, если там есть хоть одна единица, то Φ выполнима. К сожалению, этот способ пригоден только для формул с небольшим числом переменных. Уже для нескольких десятков и сотен переменных он не годится из-за большого размера получающейся таблицы - нетрудно подсчитать, что число 290 превосходит количество атомов во всей видимой вселенной.
В математической логике построены аксиоматические системы, позволяющие формализовать человеческие рассуждения о выводимости одних тождественно истинных формул из других (см., например, [15]). В некоторых случаях они позволяют доказать тождественную истинность достаточно длинных формул, имеющих регулярную структуру. Но в общем случае и они практически не применимы для произвольных формул с большим числом переменных.
В теории сложности алгоритмов имеется ряд результатов (они выходят за рамки нашего курса), которые свидетельствуют о том, что эффективных алгоритмов для проверки выполнимости или тождественной истинности произвольной булевой формулы не существует. Вместе с тем для некоторых подклассов формул эти задачи решаются достаточно эффективно. Один такой подкласс - Хорновские формулы - будет рассмотрен далее в лекции 6
Эквивалентность булевых формул
Определение 4.1. Булевы формулы Φ и Ψ называются эквивалентными, если соответствующие им функции fΦ и fΨ равны.
Обозначение: Φ Ψ. Эквивалентные формулы называют также тождественно равными, а выражения вида Φ Ψ логическими тождествами .
Основные эквивалентности (тождества)
Таким образом, эквивалентные формулы являются различными заданиями одной и той же булевой функции. Ниже мы приводим ряд пар эквивалентных формул (тождеств), отражающих существенные свойства логических операций и важные соотношения между различными операциями. Они часто позволяют находить для булевых функций по одним задающим их формулам более простые формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.
Пусть ˆ - это одна из функций , , +. Для этих трех функций выполнены следующие две эквивалентности (законы ассоциативности и коммутативности).
Ассоциативность:
-

(1)
Коммутативность:
-

(2)
Дистрибутивные законы:
-
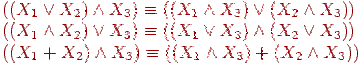
(3)
Двойное отрицание:
-
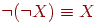
(4)
Законы де Моргана (внесение отрицания внутрь скобок):
-
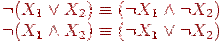
(5)
Законы упрощения:
-

(6)
Некоторые
законы упрощения имеют собственные
названия: эквивалентности в первой
строке называются законами идемпотентности,
![]() -
это закон противоречия,
-
это закон противоречия,
![]() -
это закон исключенного третьего.
Эквивалентности в двух последних строках
иногда называют законами 0 и 1.
-
это закон исключенного третьего.
Эквивалентности в двух последних строках
иногда называют законами 0 и 1.
Следующие две эквивалентности позволяют выразить импликацию и сложение по модулю 2 через дизъюнкцию, конъюнкцию и отрицание.
|
(7) |
|
|
|
(8) |
||
|
|
|
|
Проверку правильности этих эквивалентностей оставляем читателям (см. задачу 4.1).
Эквивалентные преобразования формул
Соглашения об упрощенной записи формул.
Законы ассоциативности показывают, что значения формул, составленных из переменных и одних операций конъюнкции, не зависят от расстановки скобок. Поэтому вместо формул ((X1 X2) X3) и (X1 (X2 X3)) мы будем для упрощения писать выражение (X1 X2 X3) , которое не является формулой, но может быть превращено в нее с помощью расстановки скобок. Аналогично, будем использовать выражения (X1 X2 X3) и (X1 + X2 + X3) для сокращения формул, состоящих из одних дизъюнкций или одних сложений по модулю 2, соответственно.
Если внешней функцией в формуле является одна из функций , , +, , то внешние скобки в записи формулы можно опустить.
Таким образом, с использованием этих соглашений формула
![]()
может быть записана как
![]()
Из определения эквивалентности формул непосредственно следует Принцип замены эквивалентных подформул:
пусть формула является подформулой формулы Φ, формула ' эквивалентна и формула Φ' получена из Φ посредством замены некоторого вхождения на '. Тогда Φ' эквивалентна Φ, т.е. Φ' Φ.
Применяя этот принцип и используя основные тождества, можно находить для заданной формулы другие эквивалентные ей формулы. Часто это может приводить к существенному упрощению исходной формулы. Например, если в формуле ((X 0) Y) заменим на основании тождеств (6) подформулу (X 0) на 0, то получим эквивалентную формулу (0 Y). По закону коммутативности (2) эта формула эквивалентна формуле (Y 0), которая, в свою очередь, по одному из тождеств группы (6) эквивалентна формуле Y. Эту цепочку эквивалентных преобразований можно записать также следующим образом:
![]()
В этой цепочке вспомогательные номера под знаками эквивалентности указывают, с помощью какой группы основных тождеств эта эквивалентность получается.
Выведем еще несколько важных логических тождеств, позволяющих проводить упрощения сложных формул. Их называют законами поглощения.
-
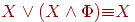
(П1)
2. Действительно,
-
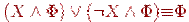
(П2)
Действительно,
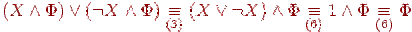
-

(П3)
Действительно,
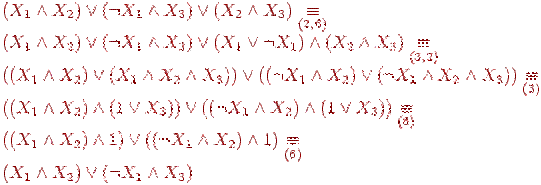
Дизъюнктивные и конъюнктивные нормальные формы
Определение ДНФ и КНФ
В этом разделе мы интересуемся представлением произвольной булевой функции посредством формул специального вида, использующих только операции , и ¬.
Пусть
![]() -
это множество пропозициональных
переменных. Введем для каждого i=1,...,n
обозначения:
-
это множество пропозициональных
переменных. Введем для каждого i=1,...,n
обозначения:
![]() и
и
![]() .
Формула
.
Формула
![]() ,
в которой
,
в которой
![]() и
все переменные разные, т.е.
и
все переменные разные, т.е.
![]() при
при
![]() ,
называется элементарной конъюнкцией
(элементарной дизъюнкцией).
,
называется элементарной конъюнкцией
(элементарной дизъюнкцией).
Определение
4.2.
Формула
![]() называется
дизъюнктивной нормальной формой (ДНФ),
если она является дизъюнкцией элементарных
конъюнкций, т.е. имеет вид
называется
дизъюнктивной нормальной формой (ДНФ),
если она является дизъюнкцией элементарных
конъюнкций, т.е. имеет вид
![]() где
каждая формула
где
каждая формула
![]() -
это элементарная конъюнкция.
называется
совершенной ДНФ, если в каждую из ее
конъюнкций
-
это элементарная конъюнкция.
называется
совершенной ДНФ, если в каждую из ее
конъюнкций
![]() входят
все
входят
все
![]() переменных
из
переменных
из
![]() Аналогично,
формула
Аналогично,
формула
![]() называется
конъюнктивной нормальной формой (КНФ),
если она является конъюнкцией элементарных
дизъюнкций, т.е.
называется
конъюнктивной нормальной формой (КНФ),
если она является конъюнкцией элементарных
дизъюнкций, т.е.
![]() ,
где каждая формула Dj
(j=1,...,r) - это элементарная дизъюнкция.
Она является совершенной КНФ, если в
каждую Dj
входят все n переменных из
,
где каждая формула Dj
(j=1,...,r) - это элементарная дизъюнкция.
Она является совершенной КНФ, если в
каждую Dj
входят все n переменных из
Совершенные ДНФ и КНФ
Рассмотрим
произвольную булеву функцию f(X1,…,Xn)
, зависящую от переменных из
![]() .
Oбозначим через Nf+
множество наборов значений переменных,
на которых f принимает значение 1, а через
Nf-
множество наборов, на которых f принимает
значение 0, т.е.
.
Oбозначим через Nf+
множество наборов значений переменных,
на которых f принимает значение 1, а через
Nf-
множество наборов, на которых f принимает
значение 0, т.е.
![]() и
и
![]()
Определим по этим множествам две формулы:
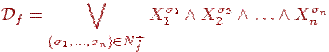
и
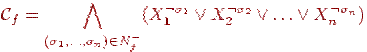
Теорема 4.1.
Если функция f не равна тождественно 0, то формула
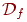 -
это совершенная ДНФ, задающая функцию
f.
-
это совершенная ДНФ, задающая функцию
f.
Если функция f не равна тождественно 1, то формула
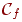 -
это совершенная КНФ, задающая функцию
f.
-
это совершенная КНФ, задающая функцию
f.
Доказательство получается непосредственным вычислением значения каждой из указанных формул с учетом того, что для любого σ {0, 1} имеют место равенства: 1σ = σ и 0σ = ¬σ (см. задачу 4.4).
Следствие 4.1.1. Каждая булева функция может быть задана формулой, содержащей переменные и функции конъюнкции, дизъюнкции и отрицания.
Приведенные выше формулы для и позволяют эффективно строить совершенные ДНФ и КН по табличному представлению функции f (Каким образом?). Можно ли получить такие специальные представления по произвольной формуле, задающей f, не выписывая ее полной таблицы? Приводимая ниже процедура позволяет это сделать, используя основные эквивалентности формул.
Процедура Приведение к совершенной ДНФ
Вход: формула Φ, включающая функции ¬, , , и +.
Используя эквивалентность (7), заменить все вхождения функции в Φ на ¬, и , затем использовать эквивалентность (8) для замены всех вхождений функции + на ¬, и .
Используя законы де Моргана (5) и снятия двойного отрицания(4), внести все знаки отрицания внутрь скобок так, чтобы все оставшиеся отрицания находились непосредственно перед переменными.
Получившаяся после шага (2) формула
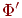 имеет
одну из двух форм:
имеет
одну из двух форм:
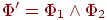 или
или
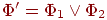 .
.
Поскольку
каждая из формул Φ1
, Φ2
имеет меньшую глубину, чем формула Φ',
то предположим по индукции, что для них
уже построены эквивалентные ДНФ
![]() и
и
![]() ,
соответственно.
,
соответственно.
Тогда в случае (а) имеем:
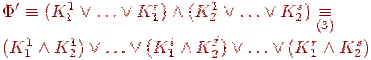
Каждый
член
![]() этой
дизъюнкции представляет собой конъюнкцию
переменных и их отрицаний. Применяя
эквивалентности групп (1), (2) и (6), можно
удалить из нее повторения переменных,
после чего она превратится в некоторую
элементарную конъюнкцию или константу.
Проделав такие преобразования со всеми
парами (i,j), 1
i
r,
1
j
s,
и удалив, если потребуется, константы
0, мы получим ДНФ, эквивалентную исходной
формуле Φ.
этой
дизъюнкции представляет собой конъюнкцию
переменных и их отрицаний. Применяя
эквивалентности групп (1), (2) и (6), можно
удалить из нее повторения переменных,
после чего она превратится в некоторую
элементарную конъюнкцию или константу.
Проделав такие преобразования со всеми
парами (i,j), 1
i
r,
1
j
s,
и удалив, если потребуется, константы
0, мы получим ДНФ, эквивалентную исходной
формуле Φ.
В
случае (б) формула
![]() сама
уже является ДНФ.
сама
уже является ДНФ.
Используя эквивалентности групп (1), (2) и (6), удалить из получившейся после шага (3) формулы повторные вхождения одинаковых конъюнкций.
Пусть после шага (4) получилась ДНФ
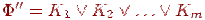 .
Чтобы получить эквивалентную совершенную
ДНФ, построим для каждой Ki
(i=1,…, m) , эквивалентную совершенную ДНФ
(см. задачу 4.5),заменим ею Ki
, а затем устраним повторения одинаковых
конъюнкций.
.
Чтобы получить эквивалентную совершенную
ДНФ, построим для каждой Ki
(i=1,…, m) , эквивалентную совершенную ДНФ
(см. задачу 4.5),заменим ею Ki
, а затем устраним повторения одинаковых
конъюнкций.
Из формулировок эквивалентностей (7) и (8) непосредственно вытекает
Предложение 4.1. На этапе (1) процедуры при последовательном выполнении преобразований (7), а затем - (8), до тех пор, пока ни одно из них не применимо, полученная в результате формула не будет содержать функций и +.
Доказательство этого предложения оставляем в виде упражнения (см. задачу 4.7).
Следующее утверждение гарантирует корректность этапа (2).
Предложение 4.2. На этапе (2) процедуры при любом порядке выполнения преобразований групп (4) и (5) до тех пор, пока ни одно из них не применимо, в полученной в результате формуле все знаки отрицания будут стоять непосредственно перед переменными.
Перед доказательством этого утверждения введем некоторые обозначения. Напомним, что в определениях 3.2 и 3.3 для каждой формулы Φ была определена ее глубина dep(Φ). Например, формула Φ=¬(X+Y) (¬(X ¬ Z) Y), построенная над системой F={ , , ¬, , +}, имеет глубину dep(Φ)=5.
Пусть Φ - это формула над F={ , , ¬}. Определим для каждой ее "отрицательной" подформулы вида ¬(Ψ) высоту h(¬(Ψ)) как 3dep(Ψ)-1 . И пусть высота всей формулы H(Φ) равна сумме высот всех ее отрицательных подформул. Например, для приведенной выше формулы Φ ее высота равна H(Φ)= h(¬(X+Y)) +h(¬(X ¬ Z))+ h(¬ Z) = (31-1) + (32-1) +(30-1) = 10.
Доказательство предложения 4.2 проведем индукцией по высоте формул.
Базис индукции. Если H(Φ)=0, то либо в Φ нет отрицаний, либо все отрицания находятся непосредственно перед переменными. Следовательно, Φ удовлетворяет требованию предложения 4.2.
Шаг
индукции.
Предположим, что при n
k
для всех формул высоты n Предложение
4.2 выполнено. Пусть Φ - произвольная
формула высоты H(Φ)= k+1. Докажем наше
утверждение для нее. Поскольку H(Φ)![]() 1, то Φ содержит хотя бы одну отрицательную
подформулу ¬(Ψ), у которой h(¬(Ψ))
1 и, следовательно, dep(Ψ)
1.
К такой формуле обязательно можно
применить либо снятие двойного отрицания
(4), либо один из законов де Моргана (5).
(Объясните
почему.)
Пусть ¬(Ψ) - это та подформула Φ, которая
на (2)-ом этапе процедуры первой заменяется
на эквивалентную формулу Ψ' в соответствии
с одной из указанных эквивалентностей.
Пусть Φ' - это формула, получившаяся в
результате этой замены из Φ. Нетрудно
проверить (проделайте эту проверку!),
что при любом из преобразований (4), (5)
H(Ψ') < H(¬(Ψ)) и, следовательно, H(Φ') <
H(Φ). Тогда H(Φ')
k и по предположению индукции применение
эквивалентностей (4), (5) в произвольном
порядке приведет в конце концов к
формуле, у которой все отрицания будут
стоять непосредственно перед переменными.
Тем самым, предложение 4.2 выполнено при
n=k+1, что завершает индукционный шаг и
все доказательство.
1, то Φ содержит хотя бы одну отрицательную
подформулу ¬(Ψ), у которой h(¬(Ψ))
1 и, следовательно, dep(Ψ)
1.
К такой формуле обязательно можно
применить либо снятие двойного отрицания
(4), либо один из законов де Моргана (5).
(Объясните
почему.)
Пусть ¬(Ψ) - это та подформула Φ, которая
на (2)-ом этапе процедуры первой заменяется
на эквивалентную формулу Ψ' в соответствии
с одной из указанных эквивалентностей.
Пусть Φ' - это формула, получившаяся в
результате этой замены из Φ. Нетрудно
проверить (проделайте эту проверку!),
что при любом из преобразований (4), (5)
H(Ψ') < H(¬(Ψ)) и, следовательно, H(Φ') <
H(Φ). Тогда H(Φ')
k и по предположению индукции применение
эквивалентностей (4), (5) в произвольном
порядке приведет в конце концов к
формуле, у которой все отрицания будут
стоять непосредственно перед переменными.
Тем самым, предложение 4.2 выполнено при
n=k+1, что завершает индукционный шаг и
все доказательство.
Рассмотрим применение процедуры приведения к совершенной ДНФ на примере.
Пример
4.1.
Пусть формула
![]() .
.
На (1)-ом этапе процедуры получаем следующую цепочку эквивалентностей:
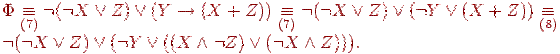
На (2)-ом этапе вносим отрицание внутрь первой скобки и получаем формулу
![]()
Устранив двойное отрицание, получим
![]()
Нетрудно видеть, что это уже ДНФ. Удалим на (4)-ом этапе повторное вхождение первой конънкции и получим ДНФ
![]()
Эта ДНФ не является совершенной, так как в каждую из ее трех конъюнкций входят не все переменные. Построим на этапе (5) для них эквивалентные совершенные ДНФ (используя решение задачи 4.5).
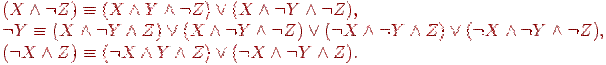
Подставив эти формулы в Φ1 и устранив повторения конъюнкций, получим совершенную ДНФ, эквивалентную исходной формуле Φ:
![]()
Мы видим, что ДНФ Φ1 , полученная после 4-го этапа, выглядит существенно проще, т.е. является более короткой, чем совершенная ДНФ Φ2 . Однако совершенные ДНФ и КНФ обладают важным свойством единственности, которое следует из их конструкции в теореме 4.1.
Следствие 4.1.2. Для каждой булевой функции от n переменных, не равной тождественно 0, существует единственная с точностью до перестановки конъюнкций и переменных внутри конъюнкций совершенная ДНФ, задающая эту функцию.
Это следствие позволяет предложить следующую процедуру для проверки эквивалентности формул Φ и Ψ.
Построить для Φ и Ψ эквивалентные совершенные ДНФ Φ' и Ψ' используя процедуру приведения к совершенной ДНФ.
Упорядочить в соответствии с нумерацией переменных X вхождения переменных в каждую конъюнкцию, а затем лексикографически упорядочить между собой конъюнкции, входящие в Φ' и Ψ'. Пусть в результате получатся совершенные ДНФ Φ'' и Ψ''
Если Φ'' = Ψ'', то выдать ответ "Да", иначе - ответ "Нет".
Замечание. Аналогичную процедуру можно построить с использованием совершенных КНФ.
