Формулы
Как мы видели, геометрическое и табличное представления булевых функций подходят лишь для функций с небольшим числом аргументов. Формулы позволяют удобно представлять многие функции от большего числа аргументов и оперировать различными представлениями одной и той же функции.
Пусть
-
некоторое (конечное или бесконечное)
множество булевых функций. Зафиксируем
некоторое счетное множество переменных
V={X1,
X2,
…} . Определим по индукции множество
формул над
с
переменными из V. Одновременно будем
определять числовую характеристику
dep(Φ) формулы Φ, называемую ее глубиной,
и множество ее подформул.
Определение 3.2.
Базис индукции. Каждая переменная Xi V и каждая константа c является формулой глубины 0, т.е. dep(Xi)= dep(c)=0 . Множество ее подформул состоит из нее самой.
Шаг индукции. Пусть
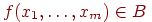и
A1,
… , Am
- формулы, и max {dep(Ai)
| i = 1,…, m} = k . Тогда выражение Φ = f(A1,…
, Am)
является формулой, ее глубина dep(Φ) равна
k+1, а множество подформул Φ включает
саму формулу Φ и все подформулы формул
A1,
…, Am.
Каждой формуле Φ(X1,…, Xn) сопоставим булеву функцию, которую эта формула задает, используя индукцию по глубине формулы.
Базис индукции. Пусть dep(Φ)=0. Тогда Φ = Xi V или Φ =c . В первом случае Φ задает функцию fΦ(Xi)=Xi, во втором - функцию, тождественно равную константе c.
Шаг индукции. Пусть Φ - произвольная формула глубины dep(Φ)= k+1. Тогда Φ(X1,…, Xn)= fi(A1,…, A_m) , где fi и A1, …, Am - формулы, для которых max1 i m{dep(Ai)}=k . Предположим (по индукции), что этим формулам уже сопоставлены функции g1(X1,…, Xn), … , gm(X1,…, Xn) . Тогда формула Φ задает функцию fΦ(X1,…, Xn) = fi(g1(X1,…, Xn), … , gm(X1,…, Xn)) .
Далее
мы будем рассматривать формулы над
множеством элементарных функций
.
Все эти функции, кроме констант, называются
логическими связками или логическими
операциями. При этом для 2-местных функций
из этого списка будем использовать
инфиксную запись, в которой имя логической
связки помещается между 1-ым и 2-ым
аргументами. Тогда определение формулы
над
имеет
следующий вид.
Определение 3.3.
Базис индукции. 0, 1 и каждая переменная Xi V являются формулами глубины 0.
Шаг индукции. Пусть Φ1 и Φ2 - формулы, ˆ { , , , +, ~, |, }.
Тогда выражения ¬ Φ1 и (Φ1 ˆ Φ2) являются формулами. При этом dep(¬ Φ1)=1 + dep( Φ1) , а dep((Φ1 ˆ Φ2))= 1 + max {dep(Φ1), dep(Φ2)} .
В соответствии с этим определением выражения Φ1(X1,X2) = ¬ (X1 ¬ X2) и Φ2(X1,X2,X3) = ( (X1 ¬ ¬ X2) (X3 ~ (X1 ¬ X2))) являются формулами. Глубина Φ1 равна 3, а глубина Φ2 равна 4. Выражения же ¬ X1 +( ¬ X2 X3) , (X1 ¬ X2) и (X1 + X2 + X3) формулами не являются (почему?).
Для определения функции, задаваемой формулой, удобно использовать таблицу, строки которой сответствуют наборам значений переменных, а в столбце под знаком каждой логической связки стоят значения функции, задаваемой соответствующей подформулой. Например, для формулы Φ2 функция fΦ2 задается выделенным столбцом следующей таблицы.
Таблица 3.4. Функция f Φ2 |
||||||||||||||
X1 |
X2 |
X3 |
((X1 |
|
¬ |
¬ |
X2) |
|
(X3 |
~ |
(X1 |
|
¬ |
X2))) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |