2.4 Форматы и стандарты цифровой записи звука

2.4.1 Цифровое представление звука Основные понятия

Фундаментом цифровой звукозаписи является преобразование непрерывного аналогового сигнала в последовательность чисел, называемых отсчетами и отображающих его амплитуду, измеряемую через равные промежутки времени. Такая процедура называется аналого-цифровым преобразованием, а устройство для ее реализации - аналого-цифровым преобразователем (АЦП).

Числа, полученные в результате аналого-цифрового преобразования, выражаются в двоичной системе исчисления, т.е. в виде комбинаций всего двух цифр - "нулей" (0) и "единиц" (1).

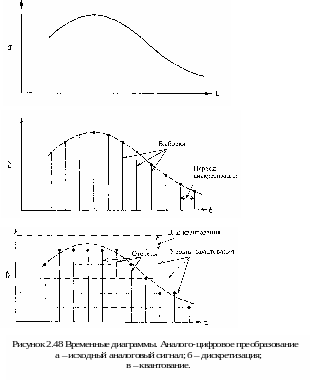
Процесс преобразования непрерывного аналогового сигнала в последовательность его мгновенных значений (выборок) называется дискретизацией (рисунок 2.48, б).

Определение численного значения величины выборки (отсчета) называется квантованием. Для этого весь диапазон возможных изменений амплитуды преобразуемого сигнала делится на множество уровней квантования, количество которых определяется разрядностью используемого при этом двоичного числа. Чем больше число разрядов квантования, тем меньше расстояние между уровнями квантования (шаг квантования) и тем выше получается точность преобразования.

В процессе квантования за величину выборки (отсчет) принимается номер ближайшего уровня квантования (рисунок 2.48, в).

В большинстве ныне существующих цифровых звуковых форматов используется 16-разрядное квантование. Это позволяет получить точность преобразования 1/2¹⁶ = 1/65536.

С числом разрядов квантования N физически связан динамический диапазон D звукового сигнала:

D=6N+1,8=6х 16+1,8=98 дБ

Следовательно, для цифровых систем звукозаписи с 16-разрядным квантованием:

D6х16+2= 98 дБ

Скорость следования отсчетов в секунду называется частотой дискретизации, а расстояние между двумя соседними отсчетами - периодом дискретизации.

Выбор частоты дискретизации в общем случае определяется известной теоремой Котельникова (теоремой отсчетов).

При этом минимально возможная частота дискретизации Fд = 2fm называется частотой Найквиста Fн.

Fн=2fm

На практике частота дискретизации Fд = (2,1 - 2,4)fm.

В зарубежной литературе в аналогичных случаях ссылаются на теорему Шеннона, которая, по сути, имеет тот же смысл, что и теорема Котельникова.

Дальнейшие рассуждения будут более понятными, если взглянуть на полную схему тракта аналого-цифрового преобразования, показанную на рисунке 2.49.

Чаще всего требуемая полоса звуковых частот ограничивается 20-22 кГц, а частота дискретизации при этом выбирается равной 44,1 или 48 кГц.

Рисунок 2.49 Схема структурная. Блок АЦП

Это связано с тем, что между наивысшей частотой звукового диапазона fm и половиной частоты дискретизации Fд/2 должен быть некоторый интервал, в который нужно поместить срез амплитудно-частотной характеристики (АЧХ) фильтра низких частот (ФНЧ), расположенного на входе блока аналого-цифрового преобразования. Этот ФНЧ, который называется анти-элайсинг фильтром, нужен для того, чтобы ни одна составляющая спектра выше Fд/2 не попала на преобразователь. Дело в том, что спектр дискретизованного сигнала обладает периодической структурой. Кроме низкочастотной части, отображающей сам звуковой сигнал, он имеет еще и высокочастотные компоненты в виде боковых полос с центрами в точках, кратных частоте дискретизации (рисунок 2.50). Если спектр звукового сигнала перед преобразованием не ограничить, то его высокочастотная часть может наложиться на смежную боковую полосу. При этом в преобразованном сигнале возникнут неустранимые искажения субдискретизации в виде паразитных высокочастотных составляющих (рисунок 2.50, б). Звучание фонограммы будет безнадежно испорчено.

П оскольку в процессе квантования отсчеты могут принимать только значения, кратные шагу квантования , то при оценке истинного значения выборки неизбежно будет возникать некоторая ошибка q (рисунок 2.51). Очевидно, что величина ошибки равна половине шага квантования и не зависит от уровня квантуемого сигнала. Функцию q(t) принято называть шумом квантования. Шум квантования будет тем ниже, чем меньше шаг квантования, или что то же самое, чем больше число разрядов квантования.

Очевидно также, что влияние шума сильно зависит от уровня преобразуемого аналогового сигнала. Если его амплитуда мала, то возникают характерные искажения, обусловленные появлением высших гармоник из-за зубчатой формы шума квантования. Причем, на слух это воспринимается именно как искажения, а не как шум.

Ослабить влияние таких искажений можно - как ни парадоксально это звучит - с помощью добавления другого шума. Если подмешать во входной сигнал так называемый "белый" шум (шум, амплитуда которого практически постоянна в широком диапазоне частот), то корреляция (связь) между шумами квантования и амплитудой сигнала нарушается. При этом воспроизведенный сигнал уже не будет выглядеть искаженным Добавление такого шумоподобного маскирующего сигнала (дифера) является весьма важной частью процесса преобразования.

Н азначение еще одного элемента тракта аналого-цифрового преобразования - устройство выборки и хранения (УВХ) ясно из его названия (рисунок 2.49). Оно предназначено для удержания значения квантуемого сигнала на время преобразования.

До сих пор речь шла о таком виде аналого-цифрового преобразования, когда расстояние между уровнями квантования одинаково во всем диапазоне изменения амплитуды преобразуемого сигнала.

Этот вид квантования называется линейным или квантованием с постоянным шагом (рисунок 2.48). Однако иногда для преобразования используют нелинейное квантование или квантование с переменным шагом. В этом случае шаг квантования увеличивается с увеличением уровня преобразуемого сигнала. Для слабых сигналов шаг квантования маленький, для сильных сигналов - большой. При прочих равных условиях такой вид квантования позволяет лучше передавать слабые сигналы, поскольку отношение сигнал/шум в этом случае будет выше, чем в случае линейного квантования.

Кроме того, нелинейное квантование позволяет значительно повысить плотность записи (или скорость передачи информации), так как малым числом разрядов можно передавать большой динамический диапазон сигнала.

На рисунке 2.52 б характеристика квантования имеет вид логарифмической кривой, что оптимальным образом отвечает условиям задачи. Но на практике реализовать такую характеристику затруднительно. Поэтому ее аппроксимируют ломаной линией, состоящей из отрезков, разбивающих весь диапазон преобразования на ряд поддиапазонов, в пределах которых шаг квантования остается постоянным. Такие поддиапазоны называются сегментами квантования (рисунок 2.52 в). Сегментов может быть от трех до 10 и более. Чем их больше, тем лучше. Но при этом реализация системы становится сложнее.

Преобразование линейной характеристики в нелинейную осуществляется после АЦП с помощью специального цифрового кодирующего устройства. Обратное преобразование в воспроизводящем (или приемном) устройстве реализуется декодером с характеристикой, представляющей собой зеркальное отражение характеристики кодера относительно линейной характеристики.

Однако, при всех своих достоинствах, нелинейное квантование имеет один очень существенный недостаток. Слабые сигналы (или обертоны) на фоне сильного сигнала (на участках характеристики с широким шагом квантования) могут сильно искажаться или даже исчезать совсем. Поэтому качество звука при нелинейном квантовании всегда хуже, чем при линейном.

Процесс обратного преобразования последовательности отсчетов в аналоговый сигнал называется цифро-аналоговым преобразованием, а устройства для его осуществления - цифро-аналоговыми преобразователями (ЦАП) (рисунок 2.53).

Н а выходе ЦАП получается ступенчатый аналоговый сигнал, величина ступенек которого равна численному значению соответствующих отсчетов. Чтобы из ступенчатого сигнала получить гладкую кривую, его необходимо пропустить через ФНЧ с характеристикой, аналогичной той, которую имел ФНЧ на входе АЦП (рисунок 2.50). Здесь так же важно, чтобы спектр звукового диапазона не перекрывался со спектром ближайшей боковой полосы, ибо это также приведет к появлению искажений.

Для этого характеристика ФНЧ должна иметь достаточно крутой срез так же, как в случае анти-элайсинг фильтра при аналого-цифровом преобразовании. Порядок такого ФНЧ должен быть не ниже 12-го. Однако построение фильтров высокого порядка связано с известными трудностями. Здесь требуется применение прецизионных пассивных элементов и высококачественных операционных усилителей с хорошей температурной и временной стабильностью. Причем, поскольку все это предназначено для использования в бытовом аппарате небольших размеров, все компоненты должны быть к тому же малогабаритными.

Кроме того, всякий фильтр высокого порядка обладает нелинейной фазовой характеристикой. А это приводит к заметным на слух искажениям звуков с крутыми перепадами уровня - барабанов, тарелок, рояля и пр.

Чтобы облегчить требования к фильтрации преобразованного сигнала, перед ЦАП устанавливается цифровой фильтр. Выполнить такой фильтр с нужными характеристиками значительно проще, чем аналоговый. Он может иметь достаточно высокий порядок и при этом обладать линейной фазовой характеристикой.

О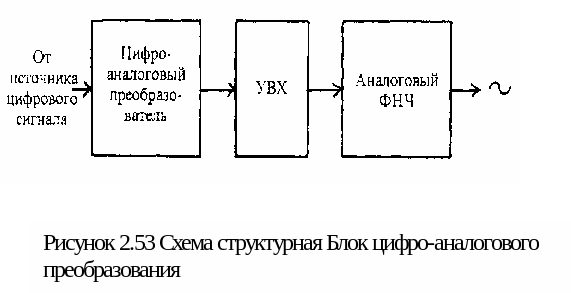 днако, характеристика цифрового фильтра, как и спектр цифрового сигнала, тоже имеет периодическую структуру и тоже повторяется на частотах, кратных частоте дискретизации. Поэтому, если цифровой фильтр будет работать на частоте дискретизации Fд, то подавить высокочастотные компоненты все равно не удастся.

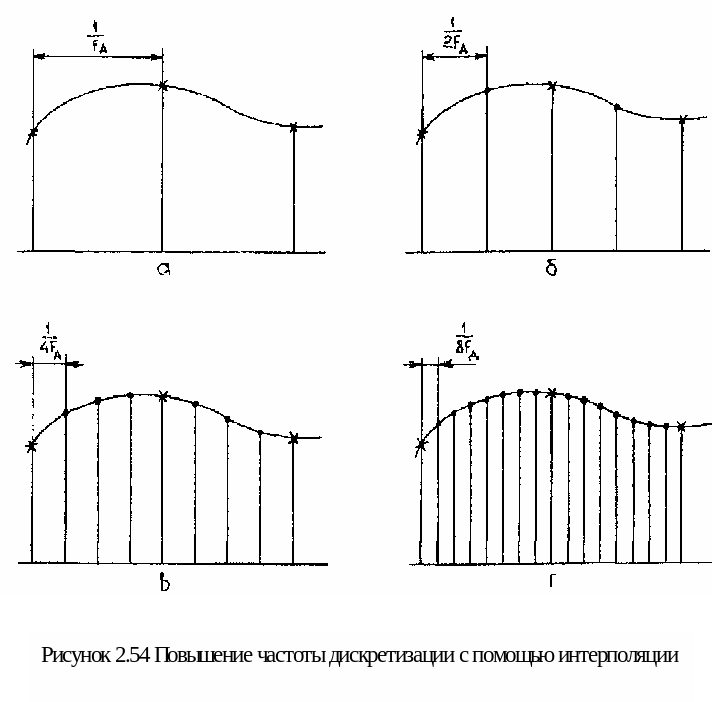
Проблема может быть решена путем искусственного увеличения частоты дискретизации Fд в несколько раз. При этом недостающие значения сигнала вычисляются по известным значениям методами интерполяции (рисунок 2.54). Схема блока цифро-аналогового преобразования в этом случае приобретет вид, показанный на рисунке 2.55.

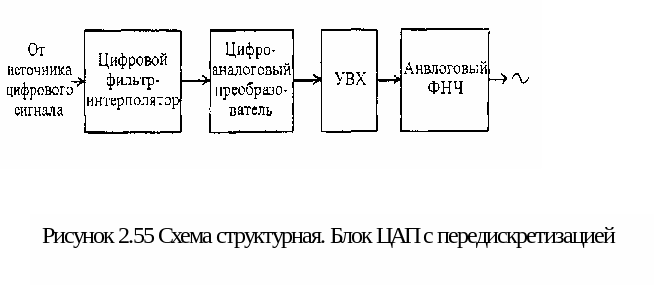
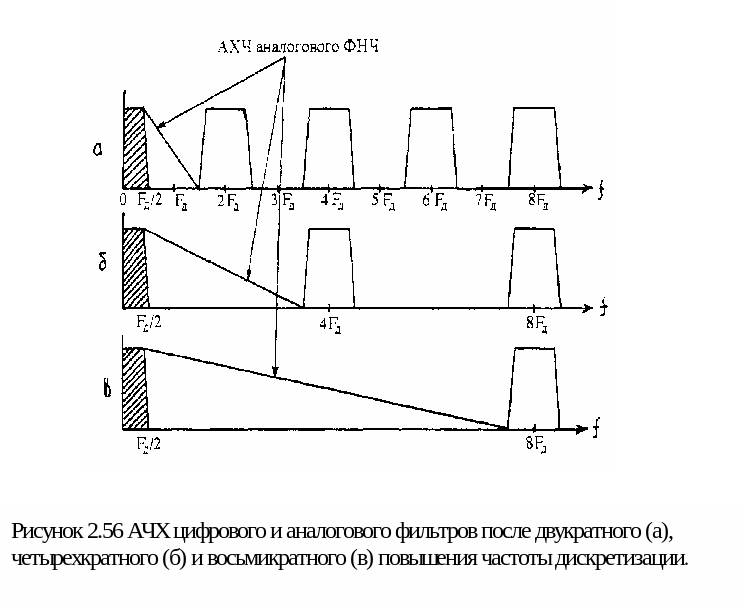
Передискретизация позволяет значительно снизить требования к характеристике аналогового ФНЧ. Даже удвоение Fд дает возможность сделать срез его АЧХ довольно пологим (рисунок 2.56, а). А при увеличении частоты дискретизации в четыре, восемь и более раз, требования к аналоговому ФНЧ снижаются до вполне заурядных (рисунок 2.56 б, в). За счет этого отношение сигнал/шум, а следовательно, и динамический диапазон, можно сделать даже большим, чем определяемая 16-разрядным квантованием величина в 98 дБ.