Индивидуальные работы студентов (микроисследования)

Помимо самостоятельной работы с литературой при подготовке к практическим занятиям и текущей аттестации, в соответствии с учебным планом и рабочей программой по дисциплине «Эконометрика» каждый студент очной формы обучения в течение семестра должен выполнить две индивидуальные самостоятельные работы по темам: «Однофакторные корреляционно - регрессионные модели и возможности их применение при анализе социально-экономических систем» и «Анализ и прогнозирование временных рядов» для закрепления навыков построения эконометрических моделей.

Индивидуальные домашние задания (ИДЗ) выдаются на лабораторных работах в начале изучения соответствующих тем. Задания индивидуальных самостоятельных работ ориентированы на освоение начального курса эконометрики, основной целью которого является овладение студентами основными методами анализа экономической информации, основанными на эконометрических моделях, концепциях и приемах. Каждый их вариантов предложенных индивидуальных самостоятельных работ имеет несколько заданий (5 заданий в индивидуальной работе №1, и 7 заданий по индивидуальной работе №2). Перед выполнением заданий рекомендуется ознакомиться с соответствующими темами указанного раздела эконометрики [1, 2, 3]:

• Парная регрессия и корреляция в эконометрических исследованиях;

• Множественная регрессия и корреляция;

• Моделирование одновременных временных рядов;

• Изучение взаимосвязей по временным рядам.

При самостоятельной работе над индивидуальными расчетными заданиями рекомендуется пользоваться Методическими указаниями, изложенными в данном пособии.

ИДЗ выполняются с использованием ППП Excel, STATISTICA и сдаются на электронных носителях в соответствующую папку на сервере, кроме того, на кафедру студенты должны сдать оформленную работу, содержащую расчеты и пояснительную записку к ней.

4. Методические указания по выполнению индивидуальных расчетных работ (микроисследований) по темам курса

Тема 1. «однофакторные корреляционно - регрессионные модели и возможности их применения при анализе социально-экономических систем ».

1.1. Методические указания

Корреляционный анализ, разработанный К. Пирсоном и Дж. Юлом, является одним из методов статистического анализа взаимозависимости нескольких признаков.

Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функций и между аргументом и функцией нельзя установить строгой зависимости, называется корреляционной.

В настоящее время корреляционный анализ (корреляционная модель) определяется как метод, применяемый тогда, когда данные наблюдений или эксперимента можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону.

После того, как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель y и аргументы x₁, x₂, …, x_k, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют точность полученного уравнения.

Т.о. регрессионная модель – это функция, описывающая зависимость между количественными характеристиками социально-экономических систем. Они строятся в тех случаях, когда известно, что зависимость между факторами существует и требуется получить ее математическое описание.

Однофакторная (парная) регрессия представляет собой регрессию между двумя переменными – у и х, т.е. модель вида

y = (x), (1)

где у – зависимая переменная (результативный признак);

х – независимая, или объясняющая, переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Линейная регрессия: y = a+bx+. (2)

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам:

• полиномы разных степеней y = a+b₁·x+b₂·x²+b₃·x³+e (3)

• равносторонняя гипербола y = a+b/x+e (4) и регрессии, нелинейные по оцениваемым параметрам:

• степенная y = ax^b ·e (5)

• показательная y = a·b^x ·e (6)

• экспоненциальная y = e ^a+b·x ·e (7)

Спецификация модели – формулировки вида модели, исходя из соответствующей теории связи между переменными. В парной регрессии выбор вида математической функции y = (x) может быть осуществлен тремя методами: графический, аналитический, экспериментальный.

Простейшей системой связи является линейная связь между двумя признаками – парная линейная регрессия. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:

Ŷ = a+bx, (8)

где ŷ – среднее значение результативного признака у при определенном значении факторного признака х;

а – свободный член уравнения;

b – коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют Метод наименьших квадратов (МНК) МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических ŷ минимальна, т.е.

 (y – ŷ)² min

С истема нормальных уравнений:

na + b x =  y

a x + b x² =  xy (9)

Можно решить эту систему уравнений по исходным данным или использовать формулы, вытекающие из этой системы:

a = (10)

b= , (10а)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_xy для линейной регрессии (-1 r_xy 1);

r_{xy= ,} (11).

Знак коэффициента корреляции показывает направление связи: «+» – связь прямая, «–» – связь обратная. Абсолютная величина характеризует степень тесноты связи. В соответствии со шкалой Чеддока:

Значения	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	св. 0,9
Сила связи	слабая	умеренная	заметная	высокая	очень высокая

Если r= 0 , то связь между факторами х и у отсутствует.

– связь функциональная.

Индекс корреляции ρ_xy характеризует силу связи в нелинейной регрессии . (0 ρ_xy 1):

ρ_{xy=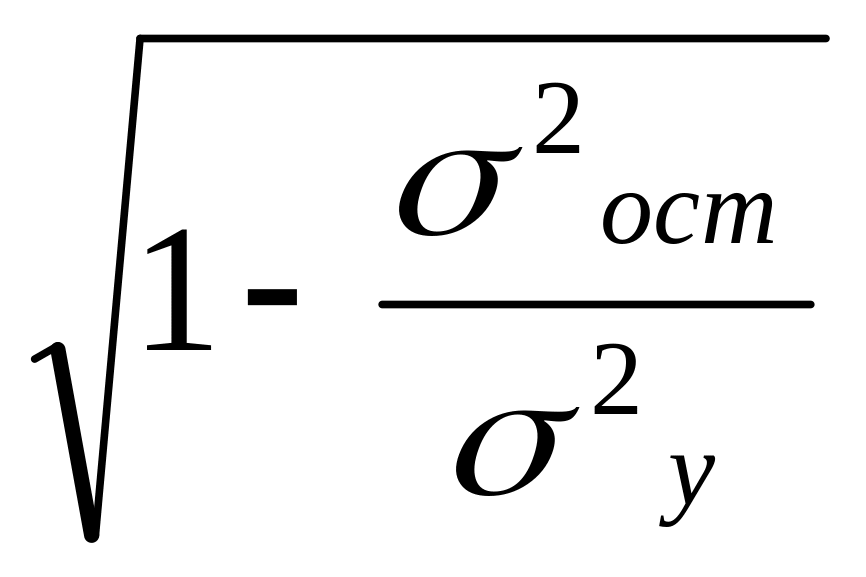 = .} (12)

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений результативного признака от фактических:

(13)

Допустимый предел значений – не более 8 – 10%.

Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:

. (14)

Для линейной регрессии

(15)

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

Правило сложения дисперсий:

å( y_i - )² = å(ŷ_x - )² + å(y_i - ŷ_x)² (16)

где å(y_i - )² – общая сумма квадратов отклонений – общая дисперсия;

å(ŷ_x - )² – сумма квадратов отклонений, обусловленная регрессией (это объясненная или факторная дисперсия)

å(y_i - ŷ_x)² – остаточная сумма квадратов отклонений.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y характеризует коэффициент (индекс) детерминации R²;

. (17)

F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

Любая сумма квадратов отклонений связана с числом степеней свободы, которое зависит от числа единиц совокупности n и числом определяемых по ней констант (переменных при х )(m).

D_общ= å( y_i - )² / (n-1)

D_факт= å(ŷ_x - )² / m (18)

D_ост= å(y_i - ŷ_x)² /n-m-1

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия:

F = D_факт/D_{ост = *} (n-2) (19)

где F-критерий для проверки нулевой гипотезы Но: D_факт = D_ост.

Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности () наличия нулевой гипотезы (уровень значимости  - вероятность отвергнуть правильную гипотезу при условии, что она верна). Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт  F_табл – Но отклоняется.

Если эта величина окажется меньше табличного, то вероятность нулевой гипотезы выше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной ошибки:

; ; (20)

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

(21)

где S²_ост – остаточная дисперсия на одну степень свободы.

(22)

сравнивая фактическое и критическое (табличное) значения t-статистики принимаем или отвергаем гипотезу Но.

Если t_табл  t_факт, то Но отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если t_табл  t_факт, то гипотеза Но не отклоняется и признается случайная природа формирования a, b, r.

Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:

∆a = t_табл m_a,

∆b = t_табл m_b (23)

Доверительные интервалы рассчитываются следующим образом:

=a ± Da =b ± Db; (24)

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значение.

Прогнозное значение результативного признака y_p определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения x_p. Вычисляется средняя стандартная ошибка прогноза

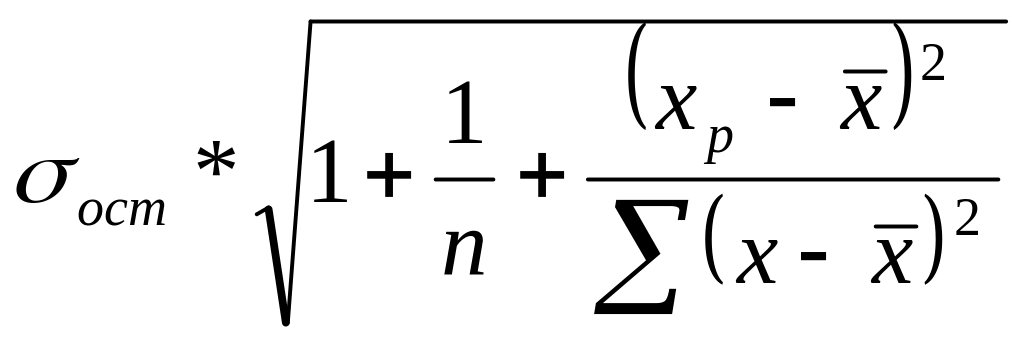= , (25)

где . (26)

Далее строится доверительный интервал прогноза:

; (27)

где (28)