
- •Основные показатели продолжительности жизни
- •Пенсионное страхование
- •План без возврата взносов.
- •2) План с возвратом взносов в случае смерти застрахованного лица в допенсионном возрасте.
- •3) План с дополнительными выплатами в случае смерти в пенсионном возрасте.
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
Основные показатели продолжительности жизни
Данные, необходимые для проведения расчетов, содержатся в таблицах смертности, или, как их еще называют, таблицах продолжительности жизни, которые представляют собой набор столбцов, отвечающих различным демографическим показателям (табл.1):
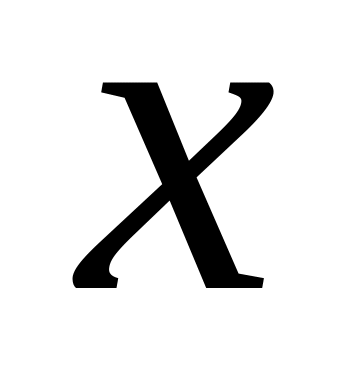 - возраст населения,
х[0,],
где
- возраст населения,
х[0,],
где
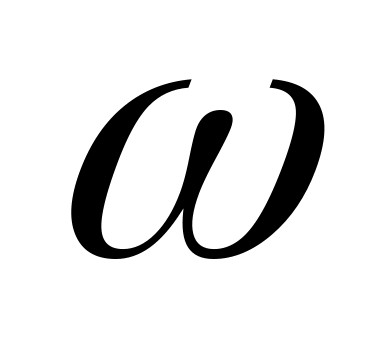 – предельный возраст, который может
быть равен 100, 110 или 120 годам. При этом
считается, что число людей в возрасте
– предельный возраст, который может
быть равен 100, 110 или 120 годам. При этом
считается, что число людей в возрасте
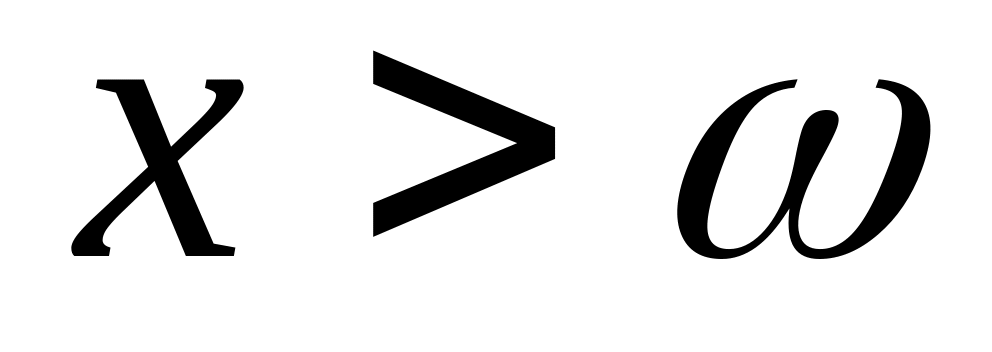 равно нулю.
равно нулю.
2.
![]() -
изменение размера когорты (выборки),
т.е. это число людей в возрасте
-
изменение размера когорты (выборки),
т.е. это число людей в возрасте
![]() (или доживших до возраста х)
из начальной совокупности (числа
родившихся)
(или доживших до возраста х)
из начальной совокупности (числа
родившихся)
![]() .
Величина
– первое значение данного столбца –
называется корнем таблицы и обычно
равно 10 000, 100 000, 1 000 000.
.
Величина
– первое значение данного столбца –
называется корнем таблицы и обычно
равно 10 000, 100 000, 1 000 000.
3.
![]() - число людей, умерших в возрасте
:
- число людей, умерших в возрасте
:
![]()
Табл.1. Фрагмент таблицы продолжительности жизни
-
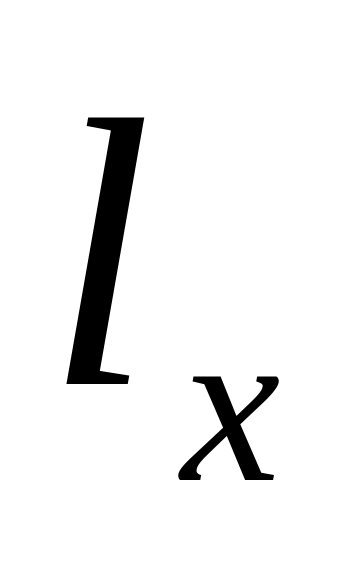
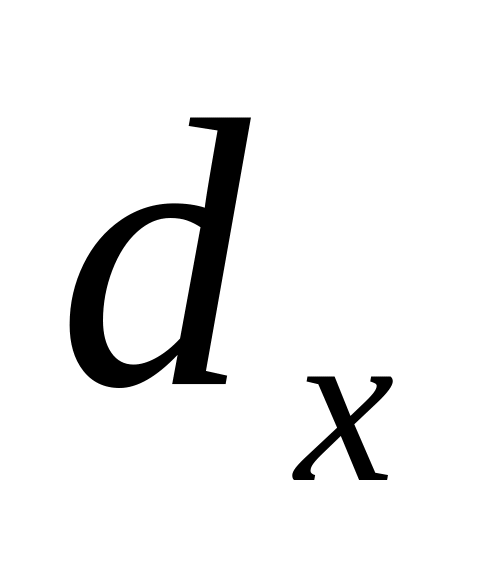
0
100000
2047
1
97953
200
…
…
…
40
83344
1145
…
…
…
100
41
41
С параметрами, указанными в таблице смертности, связаны величины, которые часто используются в актуарных расчетах.
Величина
![]() -
вероятность умереть в течение года для
человека в возрасте х
лет - может быть определена следующим
образом:
-
вероятность умереть в течение года для
человека в возрасте х
лет - может быть определена следующим
образом:
![]() .
.
Тогда величина
![]() -
вероятность дожить до возраста
-
вероятность дожить до возраста
![]() для человека в возрасте х
лет:
для человека в возрасте х
лет:
![]() .
.
Обозначив через
![]() вероятность прожить еще n
лет для человека в возрасте х,
получим:
вероятность прожить еще n
лет для человека в возрасте х,
получим:
![]() .
.
Отсюда вероятность
для человека в возрасте
умереть в течение следующих n
лет:
![]() .
.
Например, через
![]() обозначается вероятность для человека
в возрасте 20 лет дожить до 90 лет; через
обозначается вероятность для человека
в возрасте 20 лет дожить до 90 лет; через
![]() - вероятность для человека в возрасте
40 лет умереть в возрасте от 40 до 60 лет
(то есть не дожить до 61 года);
- вероятность для человека в возрасте
40 лет умереть в возрасте от 40 до 60 лет
(то есть не дожить до 61 года);
Введем еще одну
характеристику продолжительности
жизни. Будем обозначать
![]() – вероятность для человека в возрасте
прожить еще s
лет и умереть в течение следующих за
тем n
лет (т.е. в возрасте от
– вероятность для человека в возрасте
прожить еще s
лет и умереть в течение следующих за
тем n
лет (т.е. в возрасте от
![]() до
до
![]() лет). Понятно, что данная вероятность
определяется как произведение вероятностей
вида:
лет). Понятно, что данная вероятность
определяется как произведение вероятностей
вида:
![]() .
.
Задача
Определить для человека в возрасте 60 лет вероятности прожить еще год; умереть в течение предстоящего года жизни; прожить еще десять лет; вероятность умереть на 14-ом году предстоящей жизни.
Пример решения.
При решении задачи будем пользоваться таблицей смертности (см. Приложение).
Вероятность прожить еще год:
![]() .
.
Вероятность умереть в течение предстоящего года жизни:
![]() (=
(=![]() ).
).
Вероятность прожить еще десять лет:
![]() .
.
Вероятность умереть на 14-ом году предстоящей жизни:
![]() .
.
Страхование сумм
Для
обозначения разного рода единовременных
платежей используется заглавная буква
А
с различными индексами, для регулярных
периодических платежей – строчная
буква а
также с различными индексами. Индексы
определяют вид и условия договора. Для
дисконтного множителя будем использовать
стандартное обозначение:
![]() ,
где i
- годовая процентная ставка. Пусть S
– страховая сумма договора. S=1
,
где i
- годовая процентная ставка. Пусть S
– страховая сумма договора. S=1
Найдем ожидаемые величины страховых выплат, то есть нетто-ставки, для основных типов страхования жизни опираясь на принцип сбалансированности обязательств страховщика и страхователя.
Пожизненное страхование.
Определим величину страхового нетто-тарифа по данному виду страхования. Пусть человек в возрасте х заключили договор на пожизненное страхование, при котором страховая сумма выплачивается выгодоприобретателю в случае смерти застрахованного лица. Найдем текущую стоимость страховых выплат.
Согласно таблицам
смертности в конце 1-ого года действия
договора страховая компания должна
выплатить сумму, равную
![]() ,
в конце 2-ого года -
,
в конце 2-ого года -
![]() ,
в конце i-ого
года –
,
в конце i-ого
года –
![]() и
т.д. Таким образом, текущая стоимость
обязательств страховщика при условии,
что
и
т.д. Таким образом, текущая стоимость
обязательств страховщика при условии,
что
![]() ,
составит
,
составит
![]() .
Поскольку сумма всех выплат должна быть
равна сумме всех взносов
.
Поскольку сумма всех выплат должна быть
равна сумме всех взносов
![]() ,
где Ах
– величина единовременного взноса
одного страхователя, получим:
,
где Ах
– величина единовременного взноса
одного страхователя, получим:
![]()
![]() .
.
Страхование жизни на срок.
Данный договор предусматривает, что страхование жизни осуществляется на определенный срок, то есть страховая сумма выплачивается выгодоприобретателю только в случае, когда застрахованное лицо не дожило до окончания срока действия договора. Следовательно, на основе полученного выше результата, величина единовременного взноса определяется по формуле:
![]() .
.
Страхование на чистое дожитие.
Согласно условиям такого договора страховая сумма выплачивается только в том случае, если человек дожил до конца срока страхования. В случае смерти страхователя в период действия договора страховая сумма не выплачивается, и взносы не возвращаются.
Определим
величину страхового тарифа. Пусть
человек в возрасте
заключили договор страхования на чистое
дожитие сроком на n
лет, и каждый человек при заключении
договора внес сумму
![]() .
Тогда страховой фонд в расчете на всех
застрахованных составит:
.
Тогда страховой фонд в расчете на всех
застрахованных составит:
![]() .
Учитывая доходность, к концу срока
страхования фонд составит
.
Учитывая доходность, к концу срока
страхования фонд составит
![]() .
Приравниваем эту величину к сумме
страховых выплат:
.
Приравниваем эту величину к сумме
страховых выплат:
![]() .
Тогда страховой нетто-тариф в расчете
на одного человека для S=1
определяется по формуле:
.
Тогда страховой нетто-тариф в расчете
на одного человека для S=1
определяется по формуле:
![]() .
.
Задача
Рассчитать размер тарифа и взноса для человека в возрасте 60 лет, заключившего договор страхования жизни сроком на три года. Норма доходности составляет 5%, а страховая сумма – 500 у.е.
Пример решения:
![]() ,
i=0.05,
S=500
,
i=0.05,
S=500
![]()
Определим размер страхового тарифа:
![]() .
.
Отсюда страховой
взнос:
![]() .
.
Коммутационные функции
Для облегчения расчета тарифов в таблицах продолжительности жизни представлены так называемые коммутационные функции, значения которых рассчитаны для фиксированной нормы доходности:
![]() .
.
![]() - ожидаемая современная стоимость
суммы страховых выплат при страховании
на дожитие до возраста x.
- ожидаемая современная стоимость
суммы страховых выплат при страховании
на дожитие до возраста x.
![]() .
.
![]() - ожидаемая современная стоимость суммы
страховых выплат при страховании рент,
начиная с возраста x.
- ожидаемая современная стоимость суммы
страховых выплат при страховании рент,
начиная с возраста x.
При страховании жизни используются функции:
![]() .
.
![]()
![]() .
.
![]()
Представим формулы для расчета тарифов по различным видам страхования, используя коммутационные функции.
1) Пожизненное страхование:
![]()
![]()
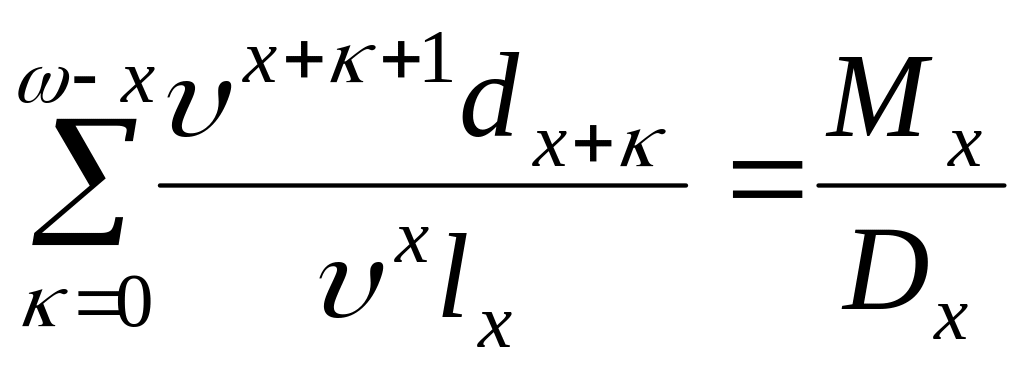
2) Страхование жизни на срок:
![]()
3) Страхование на чистое дожитие:
![]()
Задача
Договор страхования заключен следующим образом: в случае, если человек после заключения договора прожил 10 лет, то он получит 10000 у.е., если он не дожил до указанного срока, то его наследники получат 6000 у.е. Определить размер единовременного страхового взноса для человека в возрасте 50 лет.
Пример решения:
В задаче рассматривается смешанное страхование жизни сроком на 10 лет с дифференцированными суммами. В этом случае величина страхового взноса будет определяться как сумма взносов по страхованию на чистое дожитие со страховой суммой 10000 у.е. и по страхованию жизни на срок со страховой суммой 6000 у.е.
1) страхование на чистое дожитие:
![]() .
.
![]() .
.
2) страхование жизни на срок:
![]() .
.
![]() .
.
Величина единовременного взноса:
![]() .
.
Страхование рент
Получение регулярного дохода во многих случаях более предпочтительно, чем единовременная выплата. Регулярные платежи через равные промежутки времени называют страховой рентой или аннуитетом. В отличие от финансовой страховая рента является условной, то есть выплаты осуществляются при условии, что застрахованный дожил до получения очередной выплаты.
Обыкновенная пожизненная рента.
Наиболее распространенным видом страховой ренты является обыкновенная пожизненная рента, при которой выплаты осуществляются в конце каждого периода жизни застрахованного. Поэтому обыкновенную ренту часто называют рентой постнумерандо.
Найдем текущую стоимость ежегодной
ренты. Пусть
человек в возрасте x
заключили договор, предусматривающий
регулярные выплаты в размере 1 у.е. в
конце каждого года жизни застрахованного.
Определим обязательства страховщика.
В конце первого года страхования
страховщик должен будет выплатить сумму
![]() ;
в конце второго года –
;
в конце второго года –
![]() и т.д. Следовательно, на момент заключения
договора суммарная текущая стоимость
будущих выплат равна:
и т.д. Следовательно, на момент заключения
договора суммарная текущая стоимость
будущих выплат равна:
![]() ,
где –
предельный возраст. Отсюда величина
единовременного взноса, который должен
заплатить страхователь при заключении
договора:
,
где –
предельный возраст. Отсюда величина
единовременного взноса, который должен
заплатить страхователь при заключении
договора:
![]() .
.
Такая рента
равносильна совокупности контрактов
на дожитие
![]() ,
так как выплаты осуществляются, если
человек дожил до конца текущего года.
,
так как выплаты осуществляются, если
человек дожил до конца текущего года.
Рента пожизненная пренумерандо.
Наряду с обыкновенной рентой часто используется приведенная рента (авансированная рента, рента пренумерандо). Выплаты по такой ренте осуществляются в начале каждого года дожития. Следовательно, по аналогии с рентой постнумерандо, величина единовременного взноса составит:
![]() ,
,
причем
имеет место равенство:
![]() .
.
3. Срочные и отложенные ренты
Рассмотренные ранее ренты являются немедленными, так как срок их действия начинается сразу после заключения договора. Срок действия отложенных (отсроченных) рент запаздывает относительно этого момента на период отсрочки, например на m лет. Примером такой отложенной ренты могут служить пенсионные выплаты.
Если срок действия договора ренты ограничен, например n лет, то рента называется срочной.
Приведем формулы для расчета современных стоимостей выплат по таким договорам в расчете на одного застрахованного.
Срочная рента постнумерандо Срочная рента пренумерандо
![]()
![]()
Отложенная рента постнумерандо Отложенная рента пренумерандо
![]()
![]()
Срочная рента постнумерандо, Срочная рента пренумерандо,
отложенная на m лет отложенная на m лет
![]()
![]()
Любая
отложенная рента представляет собой
совокупность двух событий: «дожить до
первой выплаты» и «получить ренту».
Значит, имеет место следующее равенство:
![]() .
.
Задача
Человек в возрасте 18 лет планирует получить высшее образование. Срок обучения – пять лет. Стоимость одного года обучения составляет 30 тыс. рублей. Какую сумму необходимо внести в страховую компанию, чтобы компания взяла на себя обязательства оплатить учебу?
Решение.
Поскольку плата вносится перед началом каждого года обучения, то договор заключается на выплату ренты пренумерандо. Величина тарифа по договору:
![]() .
.
![]() .
.
Ренты, выплачиваемые несколько раз в год
Ежегодные ренты встречаются реже, чем ренты, выплачиваемые несколько раз в год (ежеквартально, ежемесячно). Страховые премии также чаще вносятся не единовременно, а ежемесячно или ежеквартально. Расчет текущих стоимостей этих рент осуществляется так же, как и в случае ежегодных рент. Будем считать, что наращение процентов происходит непрерывно и для промежуточных значений численности доживающих используется линейная интерполяция.
Рассмотрим срочную авансированную ренту.
Пусть выплаты
осуществляются q
раз в год, и за год выплачивается сумма,
равная 1 у.е. Следовательно, величина
каждой выплаты равна
![]() .
Тогда текущая стоимость ренты определяется
следующим равенством:
.
Тогда текущая стоимость ренты определяется
следующим равенством:
![]() .
.
Так как величина i мала, то для дисконтного множителя и числа доживающих справедлива интерполяция в пределах года:
![]()
Подставим данное выражение в сумму, получим:
![]()
где p – индекс числа долей, q – число выплат в году.
Задача
Страхователь в возрасте 45 лет заключает договор смешанного страхования жизни сроком на 20 лет. Определить ежегодную и ежемесячную премии (взносы), которые необходимо вносить страхователю в течение первых 5-ти лет при страховой сумме 2000 единиц.
Решение.
Заданы следующие параметры: х = 45, S = 2000, n = 20, m = 5, q = 12.
Определим величину единовременного взноса (стоимость контракта). Для смешанного страхования она вычисляется по формуле:
![]() ,
где
,
где
![]() ,
,
![]() .
.
Получили:
![]()
Найдем величину ежегодного взноса. Для этого рассчитаем коэффициент рассрочки:
![]() .
.
Тогда премия, уплачиваемая страхователем в начале каждого года уплаты взносов, составит:
![]() .
.
Определим величину ежемесячных выплат. В этом случае коэффициент рассрочки будет рассчитываться по формуле:
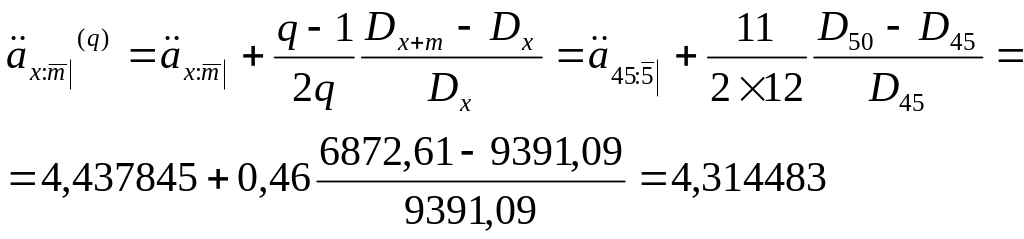
![]()
Тогда размер
ежемесячной выплаты составит
![]() .
.
В этом случае
суммарная выплата за год будет превышать
размер ежегодной премии:
![]() .
.
