Виды игр (безкоалиционные, кооперативные, дифференциальные и другие).

кооперативные Теория игр занимается изучением конфликтов, то есть ситуаций, в которых группе людей необходимо выработать какое-либо решение, касающееся их всех. Некооперативная теория игр изучает то, как должны действовать игроки, чтобы прийти к тому или иному результату, кооперативная же теория игр изучает вопрос о том, какие исходы достижимы и условия достижения этих исходов.

Согласно определению, кооперативной игрой называется пара (N,v), где N — это множество игроков, а v — это функция: 2^N → R, из множества всех коалиций в множество вещественных чисел (так называемая характеристическая функция). Предполагается, что пустая коалиция зарабатывает ноль, то есть v(∅) = 0. Характеристическая функция описывает величину выгоды, которую данное подмножество игроков может достичь путем объединения в коалицию. Подразумевается, что игроки примут решение о создании коалиции в зависимости от размеров выплат внутри коалиции.

• Монотонность — свойство, при котором у больших (в смысле включения) коалиций выплаты больше: если  .

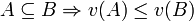• Супераддитивность — свойство, при котором для любых двух непересекающихся коалиций A и B сумма их выгод по отдельности не больше их выгоды при объединении:

• Выпуклость — характеристическая функция является выпуклой:

Простые игры — особый вид кооперативных игр, где все выплаты это 1 или 0, то есть коалиции либо «выигрывают», либо «проигрывают». Простая игра называется правильной, если:

.

Значение этого: коалиция выигрывает тогда и только тогда, когда дополняющая коалиция (оппозиция) проигрывает.

В соответствии с определением кооперативной игры, множество игроков N в совокупности обладает некоторым количеством определенного блага, которое надлежит разделить между участниками. Принципы этого деления и называются решениями кооперативной игры.

Решение может быть определено как для конкретной игры, так и для класса игр. Естественно, что наибольшей важностью обладают как раз те принципы, которые применимы в широком спектре случаев (то есть для обширного класса игр).

Решение может быть как однозначным (в этом случае для каждой игры решением является единственное распределение выигрышей), так и многозначным (когда для каждой игры могут быть определены несколько распределений). Примерами однозначных решений служат N-ядро и вектор Шепли, примерами многозначных — C-ядро иK-ядро.

Дифференциальные игры — раздел математической теории управления, в котором изучается управление объектом в конфликтных ситуациях (см. теория игр). В дифференциальных играх возможности игроков описываются дифференциальными уравнениями или дифференциальными включениями, содержащими управляющие векторы, которыми распоряжаются игроки. Для выбора своего управления каждый игрок может использовать лишь текущую информацию о поведении игроков. Различают дифференциальные игры двух игроков и многих игроков.

Наиболее исследованными являются дифференциальные игры преследования, в которых количество игроков равно 2, одного называют догоняющим, другого убегающим. Цель догоняющего — приведение вектора   на заданное множество   за возможно короткое время; цель убегающего — по возможности оттянуть момент прихода вектора   на  . Основополагающие результаты в дифференциальных играх получены в 60-е гг. 20 в. в СССР Л. С. Понтрягиным, Н. Н. Красовским,Е. Ф. Мищенко, Б. Н. Пшеничным и др., в США — Р. Айзексом, Л. Берковицем, У. Флемингом и др.

Первым, кто исследовал дифференциальные игры, стал Руфус Айзекс (работа 1951 года, впервые опубликована в 1965 году). А одна из первых проанализированных им игр стала игра «Шофёр-убийца» (homicidal chauffeur game). Надо отметить, что сам Айзекс вместо «шофёра» и «пешехода» подразумевал торпеду и увёртывающийся от неё небольшой катер.^[1]