3. Общая формулировка и существование

решения задач линейного программирования

В реальных задачах линейного программирования может быть очень много плановых показателей. В любом случае, однако, требуется найти наиболее выгодный вариант в опре­деленной экономической ситуации. С чисто математической стороны требуется найти значения нескольких неизвестных так, чтобы:

1)эти значения были неотрицательны;

2) эти значения удовлетворяли системе линейных уравне­ний или линейных неравенств;

3) при этих значениях некоторая линейная функция имела минимум (или максимум).

Определение линейного программирования

Линейное программирование — это математическая дис­циплина, изучающая методы нахождения экстремального значения линейной функции нескольких переменных при условии, что последние удовлетворяют конечному числу ли­нейных уравнений и неравенств.

Запишем это с помощью формул. Дана система линейных уравнений и неравенств:

(3)

и линейная функция

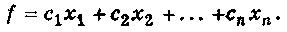
(4)

Требуется найти такое неотрицательное решение

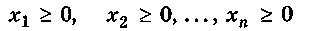
(5)

системы (3), чтобы функция f принимала наименьшее (или наибольшее) значение. Условия (3) называют огра­ничениями данной задачи, а функцию f — целевой функ­цией (или линейной формой).

Заметим, что ограничения в виде неравенств всегда мож­но свести к ограничениям в виде уравнений (способом введе­ния добавочных переменных). Так, для неравенства

(6)

введя добавочную переменную x_n+1, получим:

(7)

Потребовав его неотрицательность наряду с неотрицатель­ностью остальных переменных, получаем, что условие превращает (7) в (6). Введя по отдельной дополнитель­ной переменной для каждого из неравенств, получим систе­му уравнений, равносильную исходной системе неравенств.

Методы линейного программирования позволяют нахо­дить экстремумы линейной функции нескольких перемен­ных при условии, что последние удовлетворяют конечному числу линейных уравнений и неравенств.

Задача линейного программирования может иметь:

единственное решение,

бесконечное множество решений, соответствующих одному и тому же (оптимальному) значению линейной функции;

не иметь решения по одной из двух причин: несовместно­сти системы ограничений или неограниченности линей­ной функции.

4. Использование средства Поиск решения табличного процессора Excel для решения задач линейного программирования

Решение задач оптимального планирования небольшого объема возможно без использования компьютера (и даже весьма полезно для того, чтобы детально разобраться в ме­тодах решения).

Однако практически важные задачи чаще всего содержат большое число переменных и ограничений, поэтому «ручное» решение становится практически невозможным. Следует либо самостоятельно составить программу для компьютера на одном из языков программирования высокого уровня, либо прибегнуть к использованию готовой программы. Такая программа, в частности, содержится в табличном процессоре Excel.

Средство, в состав которого входит программа оптимизации, называется Поиск решения. Соответствующая команда находится в меню Сервис. Поиск решения - одно из самых мощных средств ТП Excel.

Рассмотрим решение задачи оптимизации на примере работы станции технического обслуживания по выполнению ТО-1 и ТО-2: системы ограничений (1) и целевой функции (2).

Вначале подготовим таблицу для решения задачи оптимального планирования. В режиме отображения формул таблица показана на рис.2

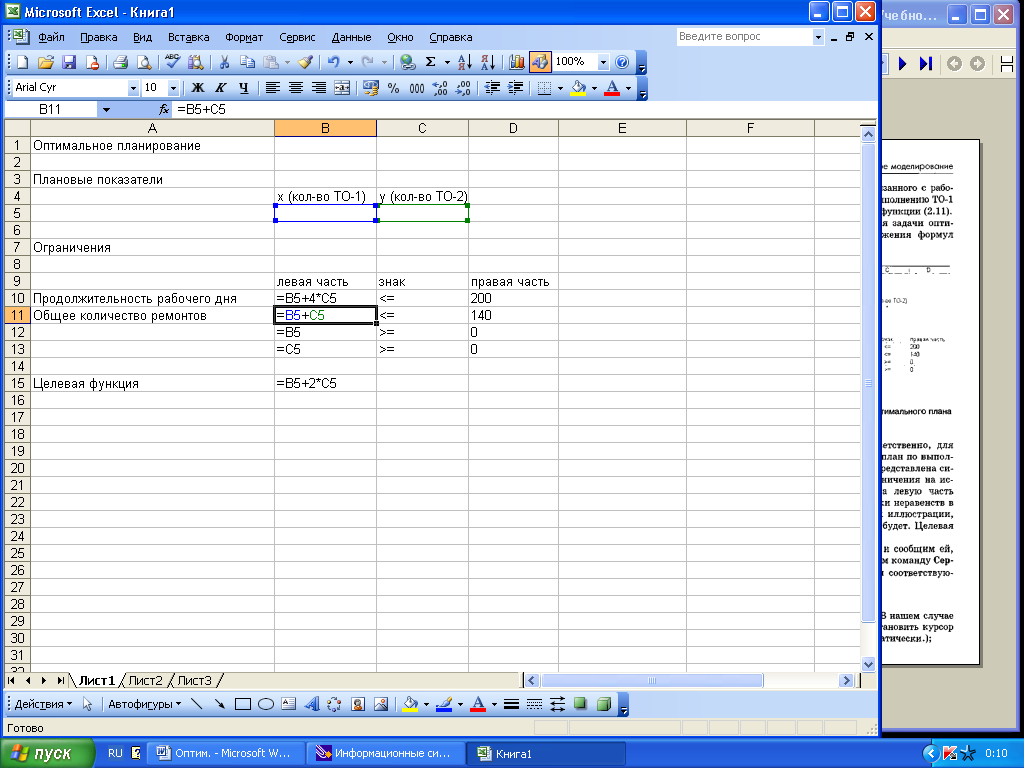
Рис.2 . Таблица, подготовленная для

расчета оптимального плана

Ячейки В5 и С5 зарезервированы, соответственно, для значений х (план по выполнению ТО-1) и у (план по выпол­нению ТО-2). Ниже в электронной таблице представлена си­стема неравенств (1), определяющая ограничения на ис­комые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С записаны исключительно в целях иллюстрации, программа ими пользоваться для работы не будет. Целевая функция (2) занесена в ячейку В15.

Теперь вызовем программу оптимизации и сообщим ей, где расположены данные. Для этого выполним команду Сер­вис- Поиск решения. На экране появится соответствую­щая форма (рис.3).

Рис. 3. Начальное состояние формы Поиск решения

Выполним следующие действия:

• введем адрес ячейки с целевой функцией (В15)

• установим флажок максимальнoму значению, т.е. сообщим программе, что нас интересует нахождение максимума целевой функции;

• в поле Изменяя ячейки введем $В5:$С5, т.е. сообщим, какое место в таблице отведено под значения переменных - плановых показателей;

• в поле Ограничения надо ввести информацию о неравен­ствах-ограничениях, которые имеют вид: $B10<=$D10; $B11<=$D11; $B12>=$D12; $B13>=$D13.

Ограничения вводятся следующим образом:

щелкнуть на кнопке Добавить;

в появившемся диалоговом окне Добавление ограничения ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10;

снова щелкнуть на кнопке Добавить и аналогично ввести второе ограничение $B11<=$D11 и т. д.;

в конце щелкнуть на кнопке ОК;

• закрыть диалоговое окно Добавление ограничения. Перед нами снова форма Поиск решения (рис.4):

Рис. 4. Форма Поиск решения после ввода информации

• теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого щелкнем на кнопке Параметры, появится форма Параметры поиска решения (рис.5);

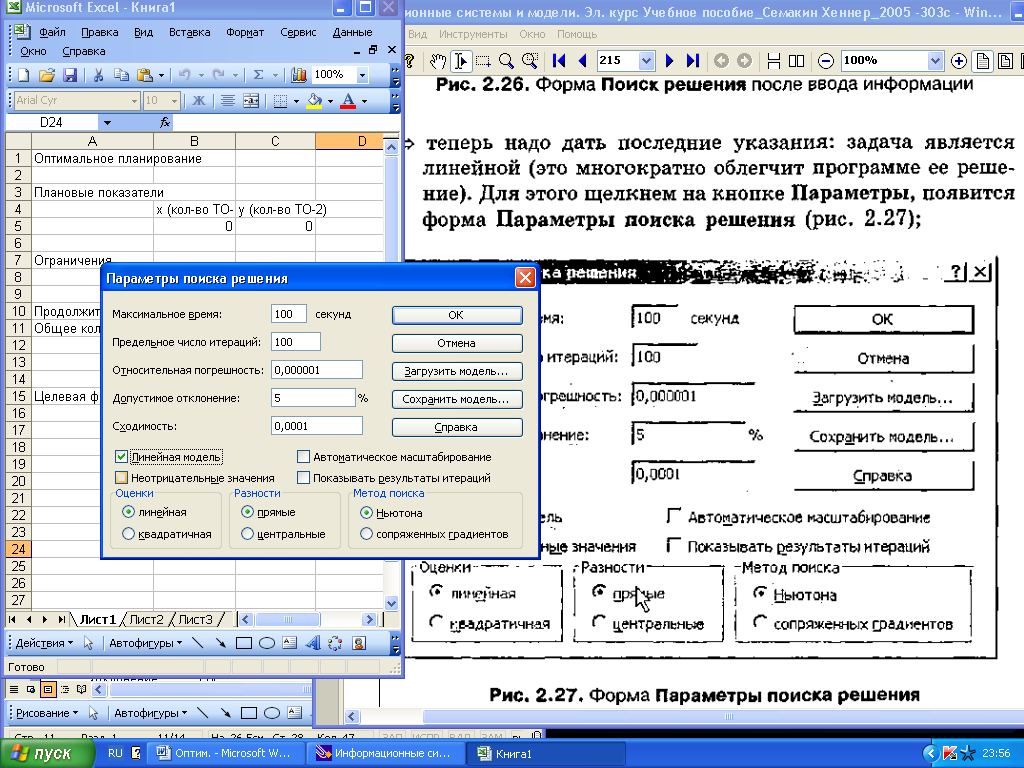
Рис. 5. Форма Параметры поиска решения

• установим флажок Линейная модель. Заметим, что было бы разумно вместо ввода двух последних ограничений, указывающих явно на неотрицательность зна­чений переменных, установить флажок Неотрицательные значения. Остальная информация в форме Параметры поиска решения служебная, устанавливаемые по умол­чанию значения нас устраивают, и вникать в их смысл не будем. Щелкнем на кнопке ОК, что возвратит нас на форму Поиск решения;

• мы ввели всю информацию. Щелкнем на кнопке Выполнить - в ячейках В5 и С5 появится оптимальное решение (числа 120 и 20), а также в ячейке В15 появится число 200 - максимальное значение целевой функции. Результат проиллюстрирован на рис. 6.

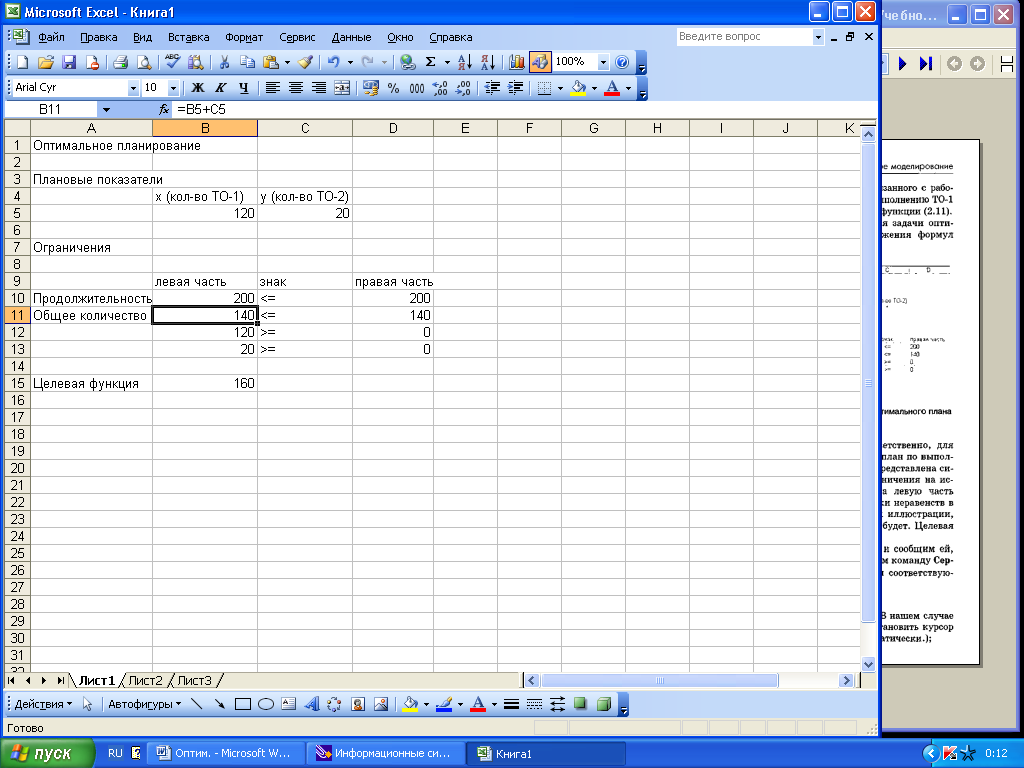
Рис. 6. Результат решения задачи

Кроме того, на экране появится еще одна форма: Результаты поиска решения (рис. 7).

Рис.7. Форма Результаты поиска решения

На первом этапе освоения возможностей программы на эту форму можно не обращать внимания (хотя в принципе в ней может оказаться очень полезная информация).

Итак, в результате применения инструмента Поиск решения станции технического обслуживания нужно выполнять 120 ТО-1 и 20 ТО-2. Эти плановые показатели соответствуют положению точки В на рис.1. В этой точке значение целевой функции f(120,20) = 200.

Полученная электронная таблица и настроенная на нее сервисная функция Поиск решения являются средством, с помощью которого можно решать задачу оптимального планирования при меняющихся условиях. Например, может измениться длина рабочего дня. Тогда надо ввести новое значение в ячейку D10, и оптимальный план автоматически пересчитается. Так же может измениться допустимое суммарное число ремонтов в ячейке D11.

Задание к лабораторной работе.