3.41. Корреляционный анализ и примеры его применения при управлении качеством

Методами корреляционного анализа устанавливается степень тес­ноты взаимосвязи между случайными величинами. Если значе­ние одной величины однозначно определяет значение другой, такие величины связаны функциональной зависимостью. Иногда значение одной величины, напротив, не зависит от того, какое значение приняла другая величина, это независимые величины. Если же известному значению одной величины соответствует не конкретное значение, а некоторое распределение другой величи­ны, то говорят, что такие величины связаны стохастической за­висимостью: такая связь имеет место в том случае, если эти вели­чины зависят не только от общих для них, но и различных случайных факторов, и эта связь может быть более или менее тесной.

Для анализа степени тесноты связи между двумя случайны­ми величинами X и Y вводится специальная характеристика, называемая ковариацией:

где m_X и m_Y — соответственно математические ожидания величин Х и Y.

Отношение ковариации к произведению стандартных от­клонений называется коэффициентом корреляции:

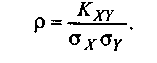
Коэффициент корреляции не превышает по модулю едини­цы и характеризует степень тесноты линейной связи между переменными X и Y. При ρ > 0 корреляция называется положи­тельной: с увеличением значений Х в среднем происходит и рост значений Y, при ρ < 0 — отрицательной. Если ρ=0, случайные величины X и Y называются некоррелированными; это не озна­чает, что эти величины не связаны между собой, но линейной связи между ними нет. При | ρ | = 1 переменные X и Y связаны функциональной зависимостью вида Y = аХ + b.

На практике считается, что при | ρ | < 0,2 линейная связь между переменными практически отсутствует, при 0,2 < | ρ | < 0,5 связь слабая, при 0,5 < | ρ | < 0,75 — средняя, при 0,75 < | ρ | < 0,95 — сильная. При | ρ | > 0,95 практически имеет место функ­циональная связь.

Пусть x_i, y_i — двумерная выборка объема n из наблюдений за случайными величинами Х и Y (i= 1, 2, ..., n). Изображая эле­менты выборки (x₁, y₁), (x₂, y₂),..., (х_n, у_n) точками плоскости в декартовой системе координат, получим диаграмму рассеяния.

Учитывая, что для выборки аналогом математического ожи­дания являются выборочные средние и , получим из первой форму­лы зависимость для расчета выборочной ковариации:

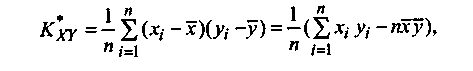
а из второй формулы — зависимость для расчета выборочного ко­эффициента корреляции

Пусть r — выборочный коэффициент корреляции, вычис­ленный по выборке объема n из генеральной совокупности, имеющей нормальное распределение. Требуется на заданном уровне значимости α проверить нулевую гипотезу о равенстве нулю коэффициента корреляции для генеральной совокупности H₀: ρ = 0.

Если нулевая гипотеза будет отвергнута, то говорят о значи­мости коэффициента корреляции, т.е. о наличии корреляции между Х и Y. Если же нулевая гипотеза принимается, то корре­ляция незначима: X и Y некоррелированы (несмотря на то, что выборочный коэффициент корреляции r 0).

Для проверки рассматриваемой гипотезы используется ста­тистика

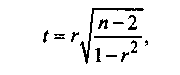
имеющая распределение Стьюдента с числом степеней свободы (n - 2).

Пример

При производственных испытаниях определяется толщина сердцевины сверла Х в мм и стойкость — время работы сверла до затупления Y в мин. Провести корреляционный анализ связи между этими показателями (табл. 5).

Таблица 5

Объем выборки n = 12. Выборочные средние:

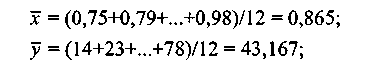
выборочный коэффициент корреляции:

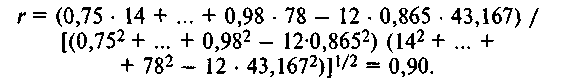
Проверим значимость корреляции: выборочное значение статистики Стьюдента:

критическое значение при правостороннем критерии на уровне значимости α=0,05:

Выборочное значение статистики попало в критическую об­ласть, нулевая гипотеза отвергается, следовательно, между тол­щиной сердцевины сверла и стойкостью имеет место сильная корреляция.

На рис. 8 показана соответствующая диаграмма рассеяния.

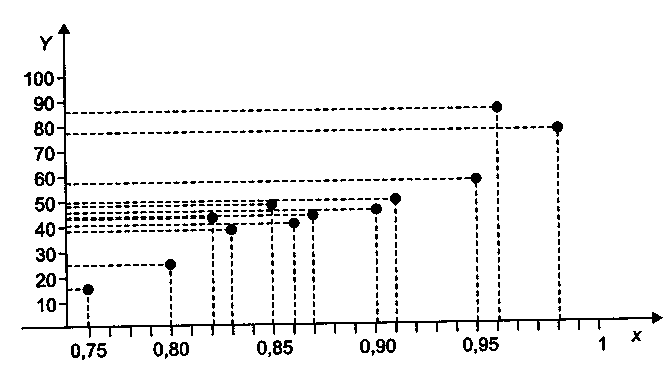
Рис. 8. Диаграмма рассеяния