1 Литературный обзор

1.1 Метод молекулярных орбиталей

1.1.1 Общие положения. Анализ с теорией многоэлектронного атома.

В 1927-1929 гг. Ф. Хунд, Дж. Леннард-Джонс и Р.С. Малликен развили идею нового подхода к поиску волновой функции молекулы, известного под названием метода молекулярных орбиталей (МО).

В методе молекулярных орбиталей рассматриваются стабильные молекулярные системы, в которых ядра находятся в равновесных положениях. С его помощью могут быть получены волновые функции, описывающие различные энергетические уровни молекул (молекулярные орбитали), на которых размещаются электроны.

Подобно атомным орбиталям, МО представляет собой одноэлектронную функцию (т.е. зависящую явно от координат только одного электрона), которая включает пространственную и спиновую компоненты- спин-орбиталь:

Каждая МО характеризуется своим значением энергии, и в соответствии с принципом построения все электроны молекулы располагаются попарно (одной пространственной функции отвечают две спиновые на МО, заполняя их в порядке повышения энергии).

Полная волновая функция молекулы, содержащей 2π электронов на n попарно заполненных МО, описывается слэтеровским определителем

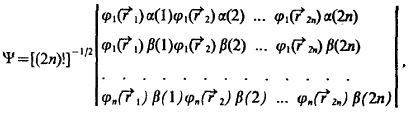
учитывающим требование антисимметрии волновой функции по отношению к перестановке любой пары электронов.

Полная энергия молекулы с волновой функцией (1.2) определяется обычным соотношением

где гамильтониан молекулы берется в приближении Борна- Оппенгеймера. Как было показано ранее, полная энергия системы электронов с волновой функцией может быть записана как

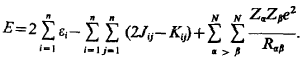
Последний член в формуле (1.4) описывает электростатическую энергию отталкивания положительно заряженных ядер атомов.

Таким образом, аппарат теории многоэлектронного атома легко переносится на случай молекулы в приближении МО и основная задача метода МО вырисовывается как нахождение пространственных функций МО, φ_і на основе которых составляется выражение (1.4).

1.1.2 Приближенное описание молекулярной орбитали в методе мо лкао

Одним из широко используемых способов приближенного описания волновой функции электрона в молекуле служит выражение МО как линейной комбинации атомных орбиталей (МО ЛКАО).

Рассмотрим электрон е в поле двух ядер А и В (Приложение А, Рисунок 1.1). В положении а на него действует поле, создаваемое обоими ядрами, но основной вклад во взаимодействие вносит ядро А, поэтому состояние электрона близко к тому, которое существует в атоме А. Его можно приближенно описать атомной орбиталью χ₁ атома А; аналогично в положении б состояние электрона приближенно описывает АО χ₂ атома В. Каждая из этих атомных функций может рассматриваться как приближенное частное решение уравнения Шредингера для электрона в молекуле АВ. Более общим решением согласно свойству уравнения Шредингера должна быть МО, являющаяся линейной комбинацией частных решений:

ψ = с₁χ₁ + с₂χ₂ (1.5)

где с₁ и с₂ – независимые параметры. Таким образом, МО строится как линейная комбинация АО, отсюда и название метода МО ЛКАО. Как видим, такая простая МО появилась на основе химической интуиции. Но в, то, же время она – простейший пример составления пробной функции в вариационном методе Релея-Ритца. На Рисунке 1.2 такая ЛКАО изображается как наложение граничных поверхностей атомных орбиталей. Это наложение особо значительно в области между ядрами. В межъядерной области происходит усиление или ослабление электронной плотности по сравнению с удвоенной атомной в зависимости от того, имеют с₁ и с₂ одинаковые или различные знаки.

Отличие электронной плотности в межъядерной области от той, которая существовала в отдельном атоме, является существенной особенностью построенной молекулярной орбитали. Выбрав при помощи вариационного метода коэффициенты с₁ и с₂ так, чтобы МО отвечала наименьшая энергия, получим лучшую из возможных функций типа ψ = с₁χ₁ + с₂χ₂. Но это не истинная волновая функция, а лишь одно из приближений; например, добавляя слагаемые в данную функцию можно получить истинную волновую функцию. Но уже и с не истинной функции можно выяснить многое из особенностей электронного строения молекул. Ее и будем использовать при изучении двухатомных молекул.

При построении молекулярной орбитали по методу ЛКАО должны соблюдаться следующие условия:

1. Комбинируемые АО должны быть близкими по энергии. Это положение может быть строго доказано, но оно и так очевидно: если АО атома А намного ниже по энергии АО атома В, то, попав в область А, электрон не перейдет в область В, так как это будет энергетически не выгодно, но останется у ядра А, и молекулярная орбиталь не образуется.

2. АО, образующие МО, должны перекрываться. При этом ядра располагаются так, чтобы перекрывание было максимальным (принцип максимального перекрывания).

Необходимость перекрывания АО очевидна. Если ядра А и В расположены так, что АО двух атомов не перекрываются, то электрон на АО атома А ни в какой достигаемой им области внутри граничной поверхности не будет испытывать действия ядра В и, значит, не сможет двигаться иначе, чем в поле ядра А. Чем полнее перекрываются АО при образовании МО, тем сильнее понижение энергии при переходе электрона с атомной на молекулярную орбиталь, тем прочнее связь, образующаяся в молекуле.

3. АО, образующие МО, должны обладать одинаковыми свойствами симметрии относительно межъядерной оси образующейся молекулы (Приложение А, Рисунок 1.3).

Совместим межъядерную ось с осью z системы координат. При этом симметрия атомных орбиталей s и p_z относительно межъядерной оси (ось z) будет одна и та же: обе орбитали не изменяют знака при повороте на любой угол вокруг оси z. Атомная орбиталь p_x отличается от них по симметрии, она изменяет, знаки своих долей на обратные при повороте на 180° вокруг оси z. Поэтому атомные орбитали s и s, p_z и s могут, а s и p_х не могут комбинировать между собой. При наложении s и p_х возникают две области перекрывания, равные по величине и противоположные по знаку, и суммарное перекрывание оказывается равным нулю.

Если эти условия не выполнены, один из коэффициентов с будет иметь очень маленькое значение, и соответствующая атомная волновая функция будет давать малый вклад в линейную комбинацию.