Заголовок

1. Назвіть умови, що мають виконуватись під час руху електрона на стаціонарній борівській орбіті. 1

2. Як можна довести, що фотон має масу? Чим вона визначається? 2

3. В чому полягає явище ізотопічного зсуву? Як його можна спостерігати експериментально? 2

4. Наскільки зміняться довжини хвиль головної та граничної ліній серії Бальмера при заміні водню на тритій? 2

5. Сформулюйте комбінаційний принцип Рітца для хвильових чисел, що відповідають лініям у спектрі випромінювання водню. 2

6. Які експерименти сприяли створенню планетарної моделі атома? 3

7. Рівняння Ейнштейна для фотоефекту. Чим визначається числове значення граничної частоти фотоефекту? 3

8. Чому максимальна енергія фотоелектронів не залежить від інтенсивності світлового потоку? 3

9. Вкажіть основні особливості комптонівського розсіяння. 3

22. Які умови накладаються на розв’язки хвильового рівняння Шредінґера? 8

23. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади. 8

24. Чим відрізняється опис атома водню в борівський теорії та в квантовій теорії? 9

25. Що таке атомна орбіталь? Наведіть приклади орбіталей для атома водню. 9

26. Який фізичний зміст квантових чисел n, l та m_l? 9

27.Що таке просторове квантування? Наведіть приклади. 10

28.Що таке спін електрона? Які експерименти підтвердили наявність спіну у мікрочастинок? 10

29.В чому полягає спін-орбітальна взаємодія? 11

30.Сформулюйте правила відбору для квантових чисел одноелектронних атомів. У чому причина появи правил відбору? 11

Позначення:

h', h — перенормована стала Планка.

1. Назвіть умови, що мають виконуватись під час руху електрона на стаціонарній борівській орбіті.

Під час руху електрона на стаціонарній борівській орбіті повинні виконуватись такі умови:

- Повна енергія електрона — незмінна: E=const ;

- Умова квантування моменту імпульсу: радіуси орбіт r повинні задовольняти умові L=mVr=nh' , де n = 1,2,… , m — маса електрона ;

- Зміна енергії електрона відбувається лише при переході електрона з однієї стаціонарної орбіти на іншу (Em -> En): h'w=Em-En , де m та n — цілі номери стаціонарних орбіт.

2. Як можна довести, що фотон має масу? Чим вона визначається?

Оскільки на фотон діє гравітаційне поле: E=mc^2 , то m(фотона)=E/c^2 .

3. В чому полягає явище ізотопічного зсуву? Як його можна спостерігати експериментально?

Ізотопічний зсув — зсув один відносно одного рівнів енергії та, відповідно, спектральних ліній в атомах різних ізотопів одного і того ж хімічного елемента, а також в обертальних та коливальних спектрах молекул, що містять ізотопи одного і того ж елемента.

4. Наскільки зміняться довжини хвиль головної та граничної ліній серії Бальмера при заміні водню на тритій?

Головна лінія:

Для водню: (хвильове число)=(стала Рідберга для водню)*(1/4 - 1/9); => (довжина хвилі)=1/(хвильове число)

Для тритію: (хвильове число)=(стала Рідберга для тритію)*(1/4 - 1/9); => (довжина хвилі)=1/(хвильове число)

Гранична лінія:

Для водню: (хвильове число) = (стала Рідберга для водню)*(1/4 - 1/(нескінченність)) => (довжина хвилі)=1/(хвильове число)

Для тритію: (хвильове число) = (стала Рідберга для тритію)*(1/4 - 1/(нескінченність)) => (довжина хвилі)=1/(хвильове число)

Отже, різниця для головної лінії — ( (стала Рідберга для водню) - (стала Рідберга для тритію) ) * 5/36, для граничної — ( (стала Рідберга для водню) - (стала Рідберга для тритію) ) * 1/4

5. Сформулюйте комбінаційний принцип Рітца для хвильових чисел, що відповідають лініям у спектрі випромінювання водню.

Комбінаційний принцип Рітца — основний закон спектроскопії, встановлений емпірично Вальтером Рітцем у 1908 році. Згідно з цим принципом все різноманіття спектральних ліній будь-якого елемента може бути представлено через комбінації якихось величин, які отримали назву терми.

6. Які експерименти сприяли створенню планетарної моделі атома?

Дослід Франка-Герца, дослід Томпсона, досліди Резерфорда, дослід Фраунгофера, спектральні серії Бальмера.

7. Рівняння Ейнштейна для фотоефекту. Чим визначається числове значення граничної частоти фотоефекту?

, де де ν — частота світла, h — стала Планка, m — маса електрона, v — його швидкість, A — робота виходу. Фотоефект спостерігатиметься лише при умові, що енергія кванту більша, або рівна роботі виходу hν ≥ A гранична частота, при якій ще можливий фотоефект νmin = A/h — частота червоної границі фотоефекту.

8. Чому максимальна енергія фотоелектронів не залежить від інтенсивності світлового потоку?

У вакуумі енергія фотона залежить від частоти імпульсу (що еквівалентно означає залежність від довжини хвилі). E=hc/(довжина хвилі). Формулу для фотоефекту можна знайти в завданні 7. З неї – максимальну енергію.

9. Вкажіть основні особливості комптонівського розсіяння.

Особливості комптонівського розсіювання:

- При копмтонівському розсіюванні фотон віддає частину своєї енергії зарядженій частинці. Як наслідок змінюється його власна енергія, а отже, довжина хвилі.

- Таке розсіювання неможливе для квантів електромагнітного поля з малою частотою.

- Енергія, втрачена фотоном при комптонівському розсіюванні, передається електрону. В результаті виникає високоенергетичний електрон віддачі.

- Комптонівське розсіювання є основним каналом розсіювання електромагнітних хвиль на речовині в області енергій від 0,5 до 3 MеВ

10. Чому ефект Комптона спостерігається лише в дослідах із рентгенівськими та γ-променями? Світло, як відомо, дифрагує на об’єктах, розмір яких порядку довжини хвилі. Тому щоб розсіяння відбувалося саме на атомах, а не на мікроскопічному пилу, довжина хвилі має бути порядку величини атома (для такої довжини хвилі частота лежить в діапазоні рентгенівських променів та γ-променів).

11. Чим визначається наявність незміщеної компоненти в розсіяних квантах в ефекті Комптона? Тим, що світло може пройти наскрізь, так і не зазнавши розсіяння на електронах або атомах матеріалу. А через те, що міжатомарна відстань набагато більша радіуса атома і товщина матеріалу дуже мала, є велика імовірність що світло таки пройде через цей матеріал не зазнавши розсіяння. 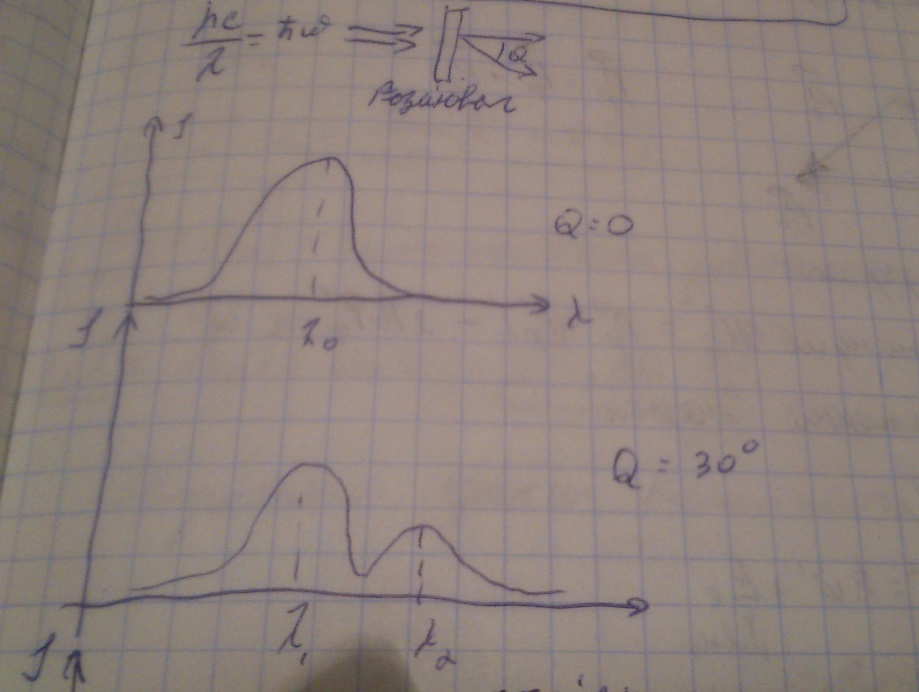- верхній графік і зображає розподіл по довжині хвилі нерозсіяних електронів. Нижній – розподіл для кута 30, де лівий «горб» - електрони, розсіяні на атомах, а правий – на електронах (електрони віддали їм частину своєї енергії, якщо я ніде не втикаю).

12. Як за дифракційною картиною в досліді Томсона якісно відрізнити аморфну речовину від кристалічної? Які зміни відбуваються, якщо під час спостереження за дифракційною картиною відбувається збільшення розмірів окремих кристаликів? Дослід Томсона (та Тартаковського) полягає в тому, що полікристалічну плівку бомбардують електронами з електронної пушки. За плівкою знаходиться чутливий до електронів екран. На екрані спостерігаємо дифракційні кільця (або точки, якщо розміри кристаликів у полікристалі досить великі). Аморфна речовина ж не буде давати дифракційних кілець Якщо збільшувати розмір окремих кристалів, то будуть спостерігатися не кільця, а світлові плями, розташовані на відповідних кільцях. - схема досліду і отримані зображення на екрані. - дифракція при розсіянні нейтронів на монокристалі NaCl (така сама картина спостерігатиметься при розсіянні електронів на полікристалі з великими розмірами кристаликів).

13. В чому полягає явище корпускулярно-хвильового дуалізму, він притаманний ансамблю, чи окремим мікрочастинкам? Відповідь обґрунтуйте. Гіпотеза, запропонована де Бройлем, про корпускулярно-хвильовий дуалізм полягала в тому, що будь яка елементарна частинка (не ансамбль) має хвильові властивості, а будь-яка хвиля має властивості, характерні для корпускули (частинки). Щодо обгрунтування, то в конспекті написано наступне: - Макрооб’єкти не проявляють хвильових властивостей в силу того, що довжина хвилі, в їх випадку, прямує до нуля через їх дуже велику масу ( , де – довжина хвилі де Бройля. , h – стала Планка, E – повна енергія , m₀ – маса об'єкту).

14. Які експерименти підтверджують наявність у мікрочастинок хвильових властивостей? Опишіть один з них. Досліди, які ми розглядати, це дослід Рамзауера (дослідження розсіювання повільних електронів інертними газами), дослід Девіссона та Джермера (дифракція елекртонів на монокристалах), дослід Томсона та Тартаковського (дифракція електронів на полікристалах). Подробиці про дослід Томсона та Тартаковського можна знайти в питанні 12.

15. Що таке хвиля де Бройля, який її фізичний зміст? Хвиля де Бройля – це хвильові властивості, які проявляють мікрочастинки. Фізичний зміст хвилі де Бройля: для важких частинок довжина хвилі мала, тому вони слабко проявляють хвильові властивості. З іншого боку частинки малої маси мають більшу довжину хвилі де Бройля, що робить можливим спостереження хвильових властивостей цих частинок (типу дифракції електронів або нейтронів). Довжину хвилі де Бройля можна знайти в завданні 13.

16. Перерахуйте основні вимоги, яким має задовольняти хвильова функція. Хвильова функція описує хвильові властивості мікрочастинок в квантовій механіці. Хвильова функція - (x, y, z, t). Тобто вона залежить від координати і часу і не має (сама по собі) фізичного змісту. Хвильова функція (або (псі)-функція) повинна мати наступні властивості: - має бути інтегровною функцією; - (x, y, z, t) – скінченна, неперервна; - якщо система може перебувати в станах , , …, , то вона може перебувати і в станах, що є лінійною комбінацією станів , , …, ( , де ). - умова нормування: – імовірність знайти частинку в усьому об’ємі, де вона може теоретично перебувати (тобто мікрочастинка завжди знаходиться в об’ємі V). - Неперервність похідних , , .

17. У чому полягає принцип суперпозиції у квантовій механіці? Наведіть приклад. Принцип суперпозиції – одна із фундаментальних засад квантової механіки. Сам принцип суперпозиції - третя умова з завдання 16 (якщо система може перебувати в станах…). Приклад (з вікіпедії): Якщо частинка може перебувати, для визначеності, в двох станах «вверх» і «вниз», вона також може перебувати в суперпозиції цих двох станів. Яким в такому випадку буде імпульс частинки – невідомо (можемо тільки оцінити імовірність частинки перебувати в тому чи іншому стані).

18. Який фізичний зміст хвильової функції? Сама по собі хвильова функція не має фізичного змісту. – імовірність знайти мікрочастинку в елементі об'єму, - елемент об’єму dx*dy*dz. – імовірність знайти мікрочастинку в елементі об’єму dV.

19. Сформулюйте співвідношення невизначеностей. Яким є їх фізичний зміст? Не можна одночасно з довільною точністю визначити проекцію імпульсу мікрочастинки і координату відносно деякої осі. , де h – перенормавана стала Планка (h = h/(2*)). Висновки: - для квантової системи стану спокою не існує; - немає розділу на кінетичну та потенціальну енергію в квантовій механіці (є повна енергія); - траєкторія частинок не актуальна. Робота іде з імовірностями та середніми значеннями.

20. В якому випадку до частинки чи ансамблю з частинок слід застосовувати квантові закони, а коли можна обмежитись класичним розглядом? Довжина хвилі де Бройля є в завданні 13. Хвильові властивості проявляють: - електрони, які пройшли різницю потенціалів меншу 1000eB ( порядку розміру ядра атома) проявляють хвильові властивості при взаємодії з речовиною. - нейтрони та протони з енергією менше 0.1 еВ (довжина хвилі де Бройля порядку величини ядра атома, теплові та холодні нейтрони) проявляють хвильові властивості при взаємодії з речовиною. Макротіла (ансамблі частинок) не проявляють хвильових властивостей через свою велику масу. Швидкі мікрочастинки (v -> c, _Б -> 0, явно корпускулярні властивості) також хвильових властивостей не проявляють (занадто мала довжина хвилі для спостереження хвильових ефектів).

21. Стаціонарне та нестаціонарне рівняння Шредінґера. Для чого вони застосовуються?

Стаціонарне рівняння: Ψ(x, y, z)

– оператор Гамільтона(оператор повної енергії), E – повна енергія.

Нестаціонарне рівння: Ψ(x, y, z, t)

- перенормована стала Планка, – оператор Гамільтона(оператор повної енергії).

Дані рівняння застосовуються для визначення власних значень фізичних величин (енергетичні спектри ) та Ψ(x, y, z, t).