17.Средняя длина свободного пробега. Экспериментальное определение поперечного сечения столкновения.

Вероятность попадания

(1) .

Это и есть метод определения поперечного сечения . Вероятность можно определить из эксперимента и тогда определим , т.е.

.

Вероятность столкновения возрастает пропорционально пути по x.

Длина пути , при которой эта вероятность равна единицы, называется средней длиной свободного пробега.

Из (1) при получаем .

Экспериментальное определение поперечного сечения столкновения

Ослабление потока частиц при пути равно числу столкновений

(2)

Решая, находим

Измерив при и можно вычислить поперечное сечение столкновений:

.

18.Частота столкновений. Модель твердых шаров.

Длина свободного пробега проходится за время

(3) .

Тогда среднее число столкновений

Пусть мишени неподвижны, а падающая частица движется со скоростью .

Из формулы (1) {} имеем , т.е.

.

Из (3) частота соударений

.

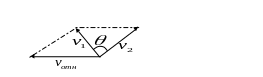
Но молекулы мишени движутся, т.е. .

.

Среднее значение относительной скорости вычислим с учетом распределения Максвелла.

Пусть z направлена вдоль .

(6)

(7)

Частота соударений между частицами в 1 м³

Для частиц с М₁ и М₂ – молярная масса

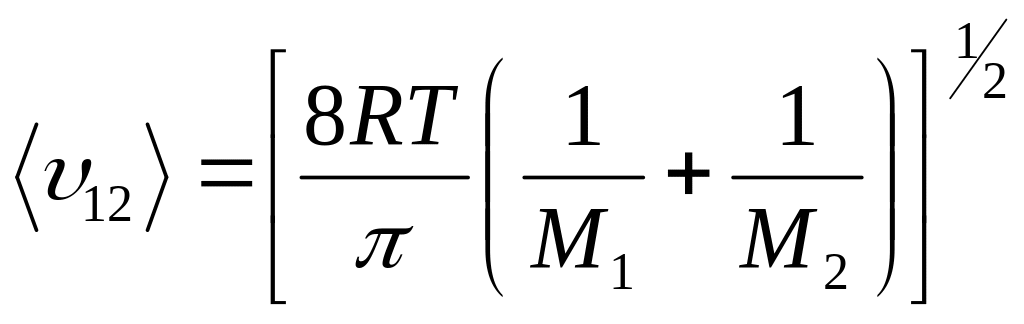
Эффективный радиус сечения столкновения равен

Обозначим частоту столкновений одной частицы 1 и частицы типа 2

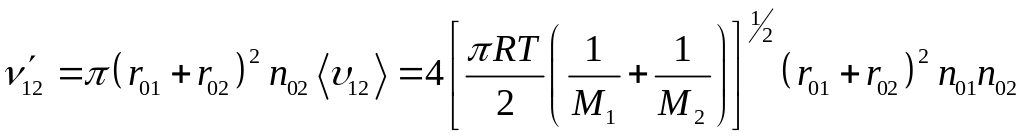
Частота соударений в 1 м³

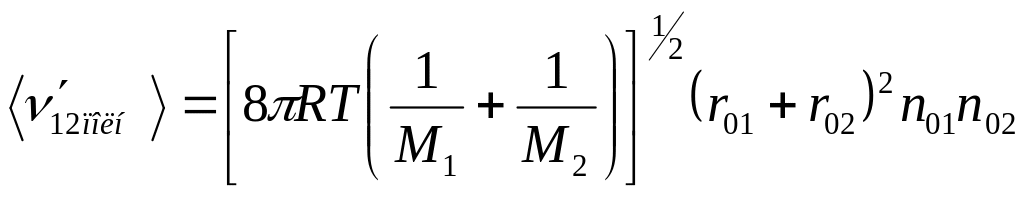
Частота столкновений частицы 2 с частицами типа 1

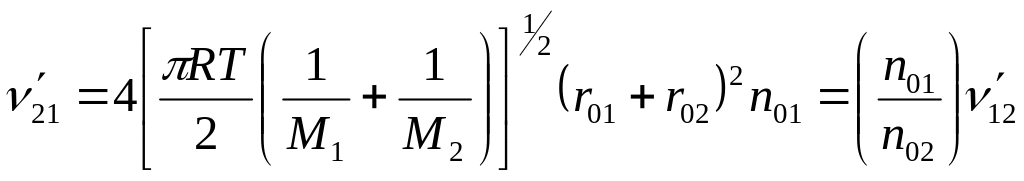
19.Экспериментальное определение длины свободного пробега.

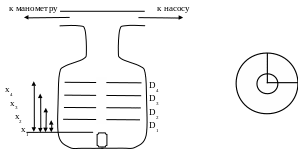
20.Барометрическая формула.

,

,

,

,

,

или для давления

Т.к.

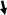
21.Подъемная сила.

Тело с жесткой оболочкой (аэростат)

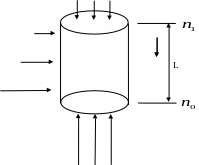
- объем цилиндра.

Т.е. сила равна весу вытесненного газа.

Рассмотрим цилиндр заполненный гелием.

С высотой концентрация частиц легкого газа (m₁) и воздуха меняются с различной скоростью

,

.

Эта подъемная сила меньше, чем сила, действующая на тело с жесткой оболочкой (аэростат) на величину равную силе тяжести легкого газа внутри цилиндра