15.Светоиндуцированный эффект.

Хаотичность движения

Равнонаправленность

Длина свободного пробега одинакова

Если бы для частиц определенного сорта длина пробега стала анизотропной, то перемещение вдоль X было бы записано в следующем виде:

,

где - частота ударов, - длина пробега вдоль X в направлении -.

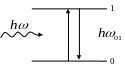
Частицы Na поглощают свет и переходят в возбужденное состояние. Сечение взаимодействия в возбужденном состоянии существенно больше.

Время жизни в возбужденном состоянии секунды.

Анизотропия создается за счет эффекта Доплера.

Если приемник движется относительно источника, то

,

где - волновой фактор, с – скорость света, звука т.д.

Пусть мы подобрали так, что имеем резонанс

.

,

где - отстройка частоты излучения от частоты перехода. Отстройку можно варьировать .

Возбужденная частица имеет больший геометрический размер и, следовательно, меньшую длину свободного пробега.

В процессе движения частица будет в резонансе только при движении в определенном направлении.

Это приведет к дрейфу частиц.

Для наблюдения эффекта необходим буферный газ, т.к. только в результате столкновений с буферным газом может проявиться анизотропия.

16.Броуновское движение. Исторические аспекты.

Движение броуновских частиц. Эксперимент Перена.

Энергия , приходящаяся на три поступательные степени свободы частицы, приводит к движению ее центра масс, которое и наблюдается под микроскопом в виде дрожания.

Случайные блуждания

, где - смещение.

.

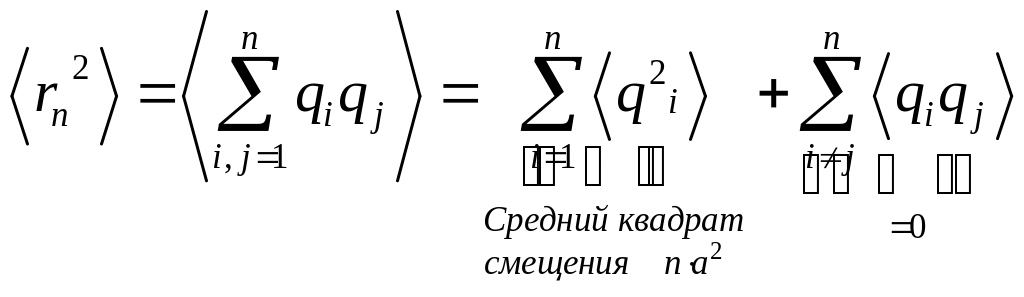Но , и - средний квадрат удаления зависит от времени линейно.

Пятно из броуновских частиц расползается.

Эксперемент Перена

Свои исследования Ж. Перрен начал с проверки основной гипотезы статистической теории А. Эйнштейна. Вооружившись микроскопом и секундомером, он наблюдал и фиксировал в освещенной камере положения одной и той же частицы эмульсии через одинаковые промежутки времени.Наблюдения показали, что беспорядочное движение броуновских частиц приводило к тому, что они перемещались в пространстве очень медленно. Частицы совершали много-численные возвратные движения. В итоге сумма отрезков между первым и последним положениями частицы была намного больше прямого смещения частицы от первой точки до последней.Ж. Перрен отмечал и потом зарисовывал в масштабе на разграфленном листе бумаги положение частиц через равные временные интервалы. Наблюдения проводились через каждые 30 сек. Соединяя полученные точки прямыми, он получал замысловатые ломанные траектории (см. рис. 6 из книги Ж. Перрена «Атомы», опубликованной в 1920 г. в Париже).Далее Ж. Перрен определил число частиц в разных по глубине расположения слоях эмульсии. Для этого он последовательно фокусировал микроскоп на отдельные слои взвеси. Выделение каждого последующего слоя осуществлялось через каждые 30 микрон. Та-ким образом, Ж.Перрен мог наблюдать число частиц, находящихся в очень тонком слое эмульсии. Частицы других слоев при этом не попадали в фокус микроскопа. Используя этот метод, ученый мог количественно определить изменение числа броуновских частиц с высотой.

Движение броуновских частиц

Уравнение движения частицы

.

Умножим на x

Т.к. 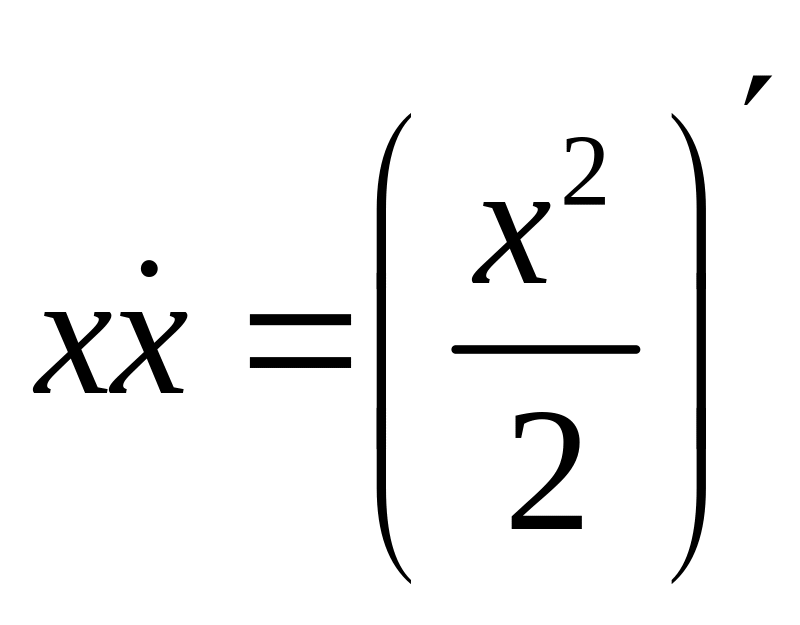и ,

.

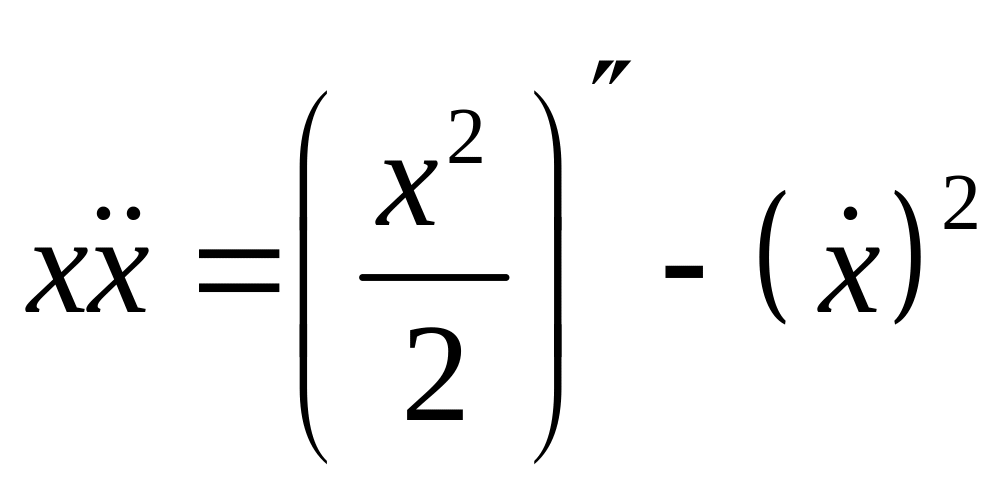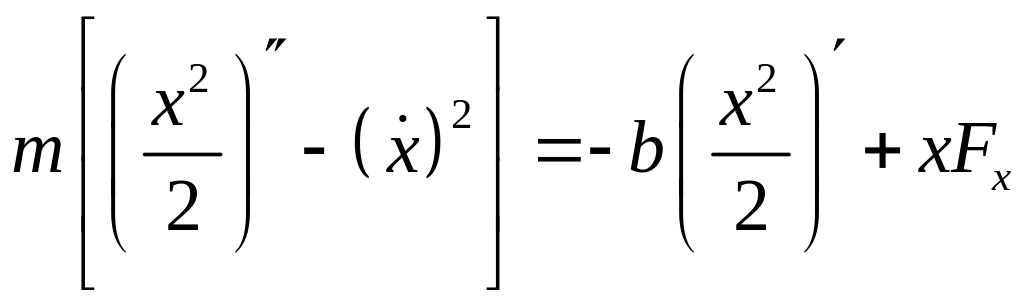Усредним по ансамблю.

Среднее от производной по времени равно производной от средней величины

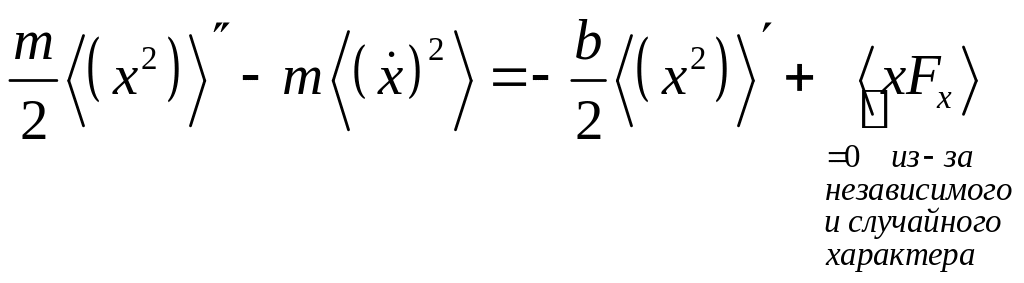
Отклонение частицы в любом направлении равновероятно, т.е.

.

Т.е. .

Таким образом, учитывая , , получим

,

где можно найти из формулы Стокса, т.е. экспериментально.

И так

Все величины известны

В 1908 г. Ж.Б. Перрен подтвердил экспериментально эти зависимости.

Известно, что , где - вязкость жидкости, - радиус шарообразной частицы.

Тяжелые частицы дрожат менее интенсивно, однако пятна из легких и тяжелых частиц расползаются с одной скоростью.

«Много движений и никаких достижений»