
- •1.Молекулярная физика, понятие молекулы, атома. Исторические сведения. Понятие статистическая физика, термодинамика.
- •2.Понятие случайного события. Совместимые, несовместимые события. Противоположные события. Достоверные события. Невозможные события. Полная группа событий.
- •3.Вероятность случайного события. Классический метод определения вероятности. Статистический метод определения вероятности.
- •4.Статистический ансамбль.
- •5.Нормировка вероятностей.
- •6.Теорема сложения и умножения вероятностей. Теорема сложения вероятностей.
- •Теорема умножения вероятностей
- •7.Плотность вероятности. Плотность вероятности
- •8.Распределение Гаусса.
- •9.Распределение Максвелла (по компонентам скорости). Распределение по вектору скорости
- •Распределение по проекции скорости
- •10.Распределение Максвелла (для модуля скорости)
- •11.Средняя скорость частиц, средняя квадратичная скорость, наиболее вероятная скорость.
- •12.Принцип детального равновесия.
- •13.Число ударов о стенку.
- •15.Светоиндуцированный эффект.
- •16.Броуновское движение. Исторические аспекты.
- •17.Средняя длина свободного пробега. Экспериментальное определение поперечного сечения столкновения.
- •18.Частота столкновений. Модель твердых шаров.
- •19.Экспериментальное определение длины свободного пробега.
- •20.Барометрическая формула.
- •21.Подъемная сила.
7.Плотность вероятности. Плотность вероятности
Если событие характеризуется непрерывными величинами, то описание осуществляется с помощью плотности вероятности.
Разделим объем V на объемы Vi (i=1, 2, 3, ...). Вероятность обнаружения молекул в выделенном объеме Vi, при N актах измерения, равна
![]() ,
где
,
где
Ni - число обнаружений молекулы в Vi.
Плотностью вероятности назовем величину, определяемую равенством
|
|
x, y, z - координаты точки, к которой стягивается бесконечно малый объем Vi.
8.Распределение Гаусса.
![]() - распределение
Гаусса.
- распределение
Гаусса.
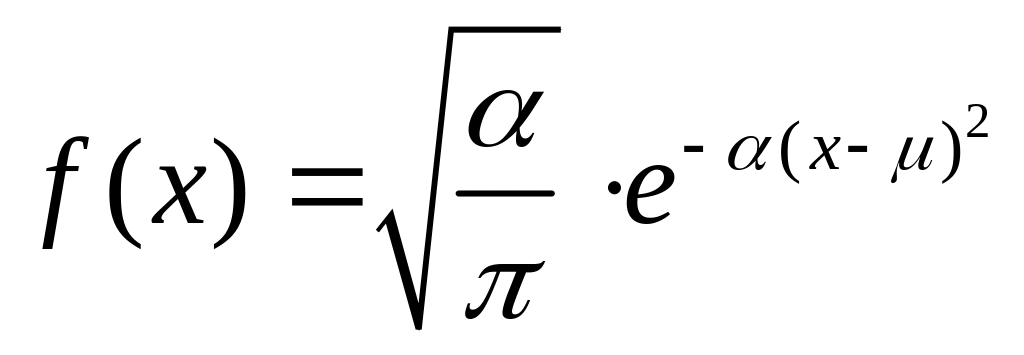 - функция
плотности вероятности.
- функция
плотности вероятности.
![]()
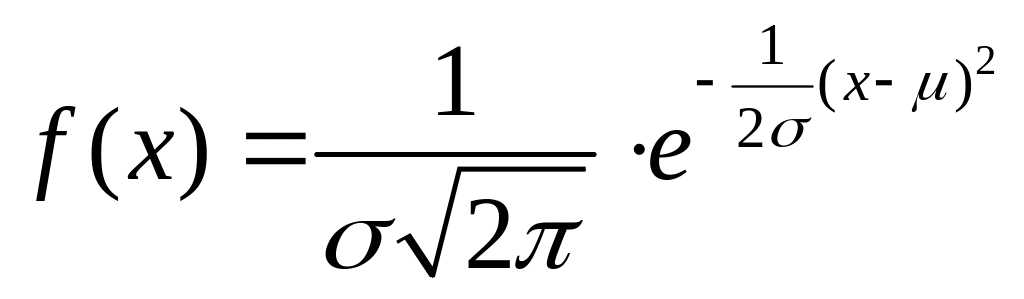
В
теоретическом распределении дисперсия
![]() есть математическое ожидание квадрата
отклонений случайной величины от её
математического ожидания
есть математическое ожидание квадрата
отклонений случайной величины от её
математического ожидания
|
Если обозначить M(x)=a, то дисперсия распределения дискретной величины может быть записана:
|
в случае непрерывной величины:
|
|
Математи́ческое ожидание — среднее значение случайной величины.
![]() ,
где N-количество
измерений
,
где N-количество
измерений
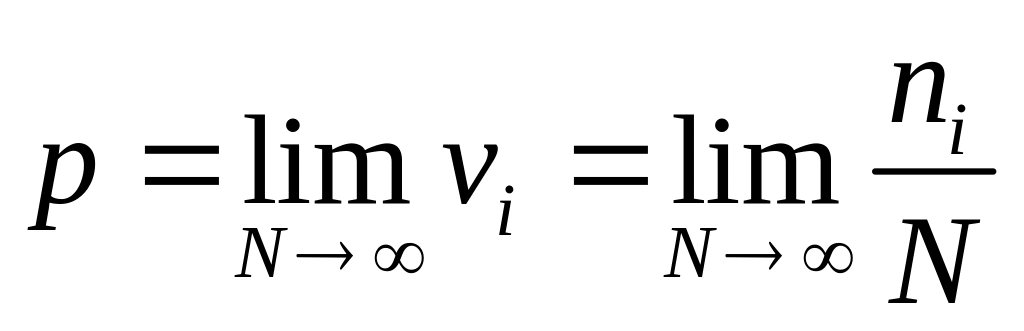 .
.
vi(частость ) — отношение частоты к объему совокупности.
9.Распределение Максвелла (по компонентам скорости). Распределение по вектору скорости
Учитывая,
что плотность распределения по
скоростям ![]() пропорциональна
плотности распределения по импульсам:
пропорциональна
плотности распределения по импульсам:
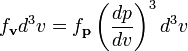
и
используя ![]() мы
получим:
мы
получим:
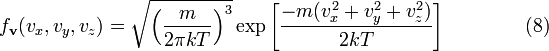
Распределение по проекции скорости
Распределение
Максвелла для вектора скорости ![]() —
является произведением распределений
для каждого из трех направлений:
—
является произведением распределений
для каждого из трех направлений:
![]() ,
,
где распределение по одному направлению:
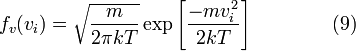
10.Распределение Максвелла (для модуля скорости)
Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:
![]()
поэтому
модуль скорости всегда будет больше
или равен нулю. Так как все ![]() распределены
нормально,
то
распределены
нормально,
то ![]() будет
иметь хи-квадрат
распределение с
тремя степенями свободы. Если
будет
иметь хи-квадрат
распределение с
тремя степенями свободы. Если ![]() — функция
плотности вероятности для
модуля скорости, то:
— функция
плотности вероятности для
модуля скорости, то:
![]() ,
,
где
![]()
таким образом, функция плотности вероятности для модуля скорости равна
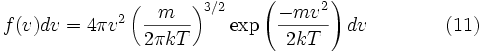
11.Средняя скорость частиц, средняя квадратичная скорость, наиболее вероятная скорость.
Средняя
скорость
![]()
Средняя
квадратичная скорость
![]()
Наиболее
вероятная скорость
![]()
12.Принцип детального равновесия.
Принцип детального равновесия утверждает, что равновесие устанавливается детально, т.е. между всеми парами элементов объема.
Число прямых и обратных столкновений в каком-то объеме одно и тоже. Для хаотического движения следует требовать, чтобы в нуль обращалась сумма взаимодействий между любыми парами объемов. Суть заключается в том, что в состоянии хаотического движения должны компенсировать друг друга любые два противоположно направленные процессы
13.Число ударов о стенку.
Плотность потока частиц вдоль X равна:
![]() ,
где
,
где
![]() - концентрация
частиц,
- концентрация
частиц,
![]() - составляющая скорости в сторону +X.
- составляющая скорости в сторону +X.
Частота ударов на единицу площади за единицу времени равна:
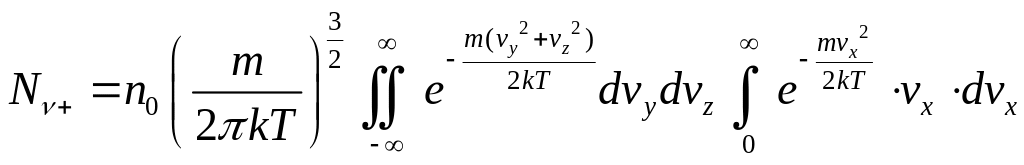 ,
,
![]() ,
,
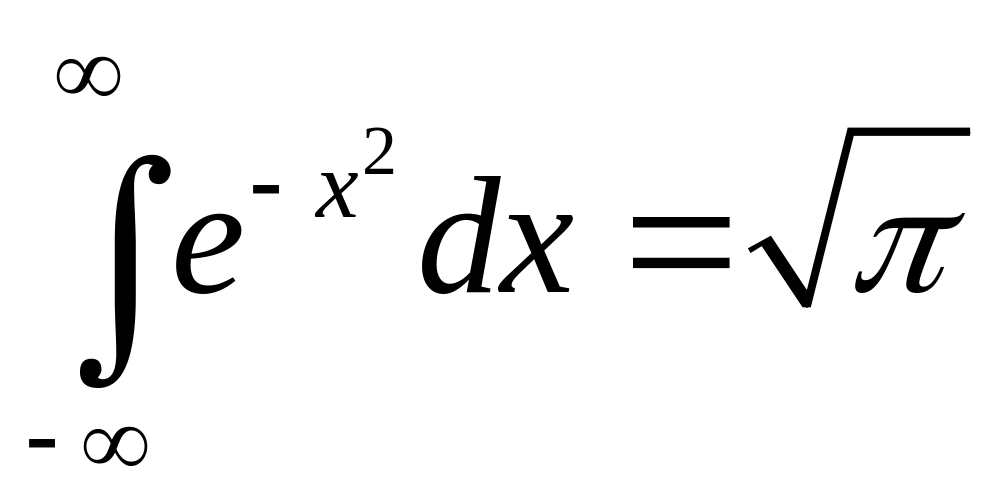
и
 .
.
Т.к.
![]() ,
,
то
![]() .
.
14.Число молекул в различных участках распределения по скоростям.
Введем новую
переменную
![]() ,
тогда
,
тогда
![]() и
и
![]() .
.
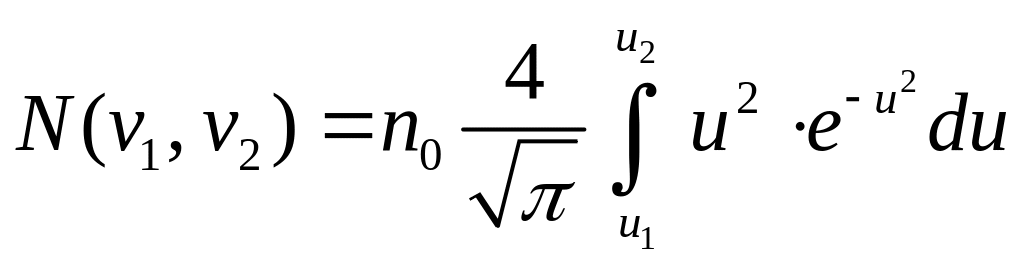 .
Этот интеграл затабулирован.
.
Этот интеграл затабулирован.

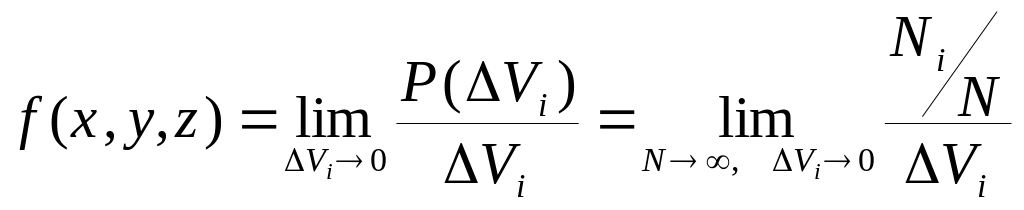 ,
где
,
где