5.Нормировка вероятностей.

. Число n_A не может бывает отрицательным, т.е. . Максимальное число благоприятных случаев появления случайного события n_A=N т.е. Р(A)=1 - вероятность достоверного события.

Суммой события А и В называется событие С, состоящее в появлении хотя бы одного из событий - либо события А либо событие В.

.

К примеру, если

A - достать из колоды даму, В - любую карту масти треф,

С - хотя бы один признак или масть треф или дама

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Если оба признака вместе (дама масти треф), то имеем произведение событий (пересечение событий):

.

Произведением двух или нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

6.Теорема сложения и умножения вероятностей. Теорема сложения вероятностей.

а) Несовместимые (взаимоисключающие) события.

Пусть событие А - появление молекулы в объеме V₁, событие В - в объеме V₂ , тогда вероятность события С - появление молекулы либо в объеме V₁ либо в объеме V₂ будет

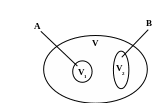
Р(C) = Р(A+B)= P(V₁ +V₂) =

=P(V₁)+P(V₂)

, т.е.

P(A+B )= P(A) + P(B).

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий.

Вероятность суммы нескольких несовместимых событий равна сумме их вероятностей.

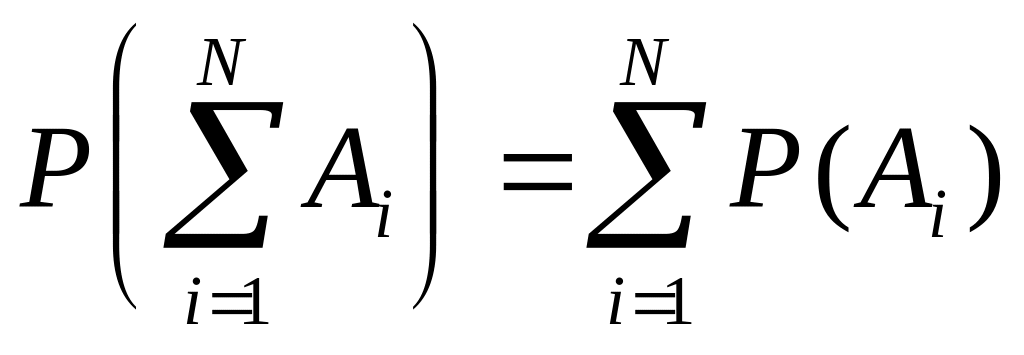
Если события А, В, С, D ... образуют полную группу, то вероятность полной группы событий равна 1, т.к. это событие достоверное.

Противоположные события образуют полную группу событий.

Пример.

Пусть Р(A + )=Р(A) +P( ) =1, Тогда

Р( ) =1-P(A).

Следовательно события А и - образуют полную группу.

б) Совместимые события

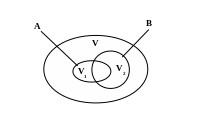
В случае, когда события A и B совместимы имеем:

Р(A)= P(V)₁ , P(B)=P(V₂).

Теперь P(C)= P(A)+P(B)= P(V₁)+P(V₂)=

Т.е. для совместимых событий справедлива формула:

Р(A+B)=P(A)+ P(B) - P(AB)

В случае когда события A_i совместимы, вероятность их суммы выражается формулой

,

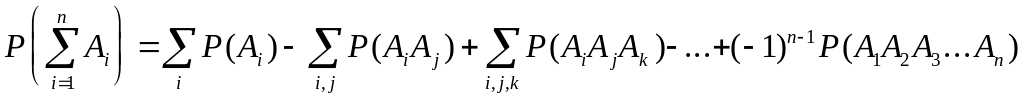где суммы распространяются на все возможные комбинации различных индексов i, j, k, ..., взятых по одному, по два, по три и т. д.

Теорема умножения вероятностей

Следует обратить внимание на понятия зависимого и независимого случайного события.

Независимыми событиями А и В будем называть события, для которых появление одного из них не зависит от того, наступило или не наступило другое событие.

В этом случае вероятность произведения событий А и B подсчитывается по формуле:

P(AB)= Р(A  B)= P(A)  P(B).

Для нескольких независимых событий

.

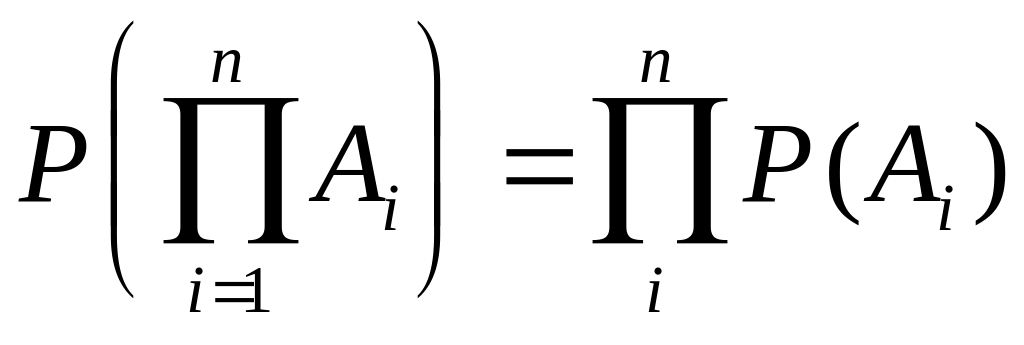Если появление события В зависит от осуществления события А, то такие события называются зависимыми. В этом случае вводится понятие условной вероятности.

Условной вероятностью события А при наличии события В называется вероятность события А, вычисленная при условии, что событие В произошло.

Эта вероятность обозначается Р(А/B).

Тогда вероятность сложного события, заключающегося в осуществлении и события А, и события В, определится как

P(AB)=Р(A  B)=P(А  В) = P(A) P(B/A), или

P(AB)= P(B) P(A/B),

т.е. как произведение вероятности события А на условную вероятность события В и наоборот.

Пример.

В урне находится "а" белых и "b" черных шаров. Некто подходит и вынимает из урны наугад по одному шару, не возвращая их обратно. Найти вероятность того, что вторым по счету будет белый шар.

Шары из урны могут быть изъяты в следующей последовательности: (чч+бч+бб+чб).

Нас интересует вероятность двух последних событий, когда вторым по счету будет белый шар, т.е.

P(бб+чб) .

Для случая нескольких событий

P(A₁A₂ ... A_n)=Р(A₁) P(A₂/A₁) P(A₃/A₁A₂) ... P(A_n/A₁A₂ ... A_n).