Минимизация дизъюнктивных нормальных форм

Булеву функцию g назовём импликантом булевой функции f, если для любых наборов значений аргументов этих функций из равенства g = 1 следует равенство f = 1. Например, для функции f из примера (*) функция является импликантом. Действительно, функция g принимает значение 1 только при x = 0, y = 1, z = 0. Но и функция f при x = 0, y = 1, z = 0 также принимает значение 1. А для функции f из примера (*) функция не является импликантом. Ведь функция g = 1 при x = 1, y = 1, z = 0. Но f(1,1,0) = 0.

Если отбрасывание любой переменной импликанта приводит к тому, что полученная функция перестаёт быть импликантом, то такой импликант называется простым. Проверим импликант на простоту. При отбрасывании в этой функции переменной x получим функцию , которая принимает значение 1 при y = 1, z = 0. Но функция f при y = 1, z = 0 может принимать и нулевое значение, например, f(1,1,0) = 0. При отбрасывании в функции переменной y получим функцию , которая принимает значение 1 при x = 0, z = 0. Но функция f при x = 0, z = 0 может принимать и нулевое значение, например, f(0,0,0) = 0. При отбрасывании в функции переменной z получим функцию , которая принимает значение 1 при x = 0, y = 1. Но функция f при x = 0, y = 1 может принимать и нулевое значение, например, f(0,1,1) = 0. Так как при отбрасывании любой переменной функция перестаёт быть импликантом функции f, то является простым импликантом функции f.

Сокращённая днф

Сокращённая ДНФ функции f есть дизъюнкция всех простых импликантов функции f.

Всякая функция реализуется своей сокращённой ДНФ. Для любой функции, не равной тождественно нулю, существует единственная сокращённая ДНФ.

Алгоритм построения сокращённой днф с помощью скнф.

1. По таблице истинности строим СКНФ функции f.

2. В СКНФ раскрываем скобки, удаляем дублирующие элементы ( , ) и элементы, которые содержат переменную вместе с её отрицанием ( ).

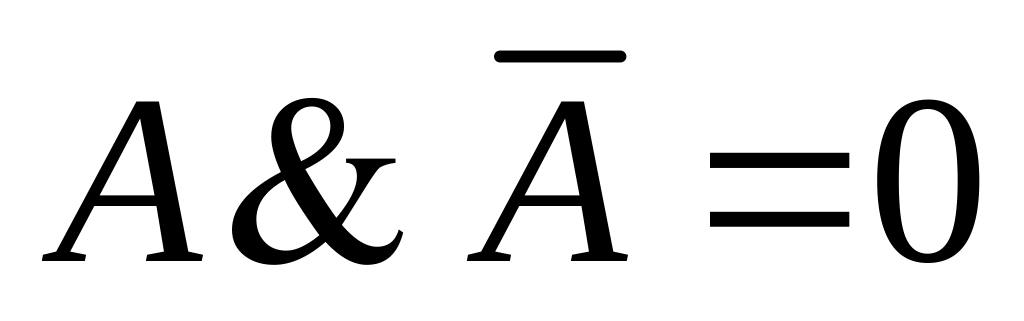3. Проводим поглощение ( 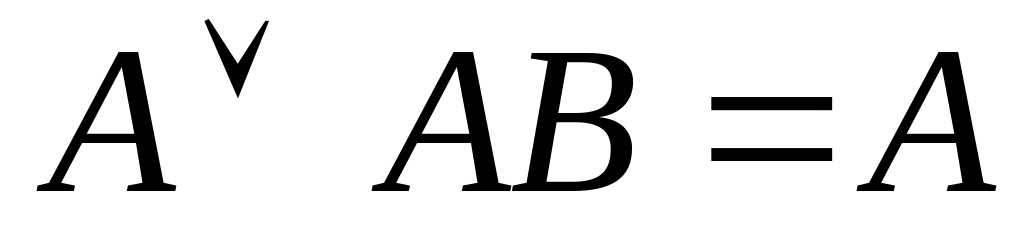) и удаляем дублирующие элементы. Сокращённая ДНФ функции f получена.

Пример.

Для функции из примера (*) построить сокращённую ДНФ.

Решение:

СКНФ .

Раскроем скобки. Перемножение лучше начинать со скобок, которые отличаются всего одной переменной. Поэтому поменяем местами вторую и третью скобки. Затем перемножим первую и вторую скобки, а также четвёртую и пятую скобки.

.

В первой скобке слагаемое y поглощает все слагаемые, содержащие y, а слагаемое z поглощает все слагаемые, содержащие z. В третьей скобке слагаемое поглощает все слагаемые, содержащие , а слагаемое поглощает все слагаемые, содержащие .

Получим . Перемножим вторую и третью скобки, так как у них есть общий элемент :

.

Мы воспользовались правилом поглощения.

Тогда .

Таким образом, получена сокращённая ДНФ функции f, то есть

сокр. ДНФ f = .

Тупиковые и минимальные днф.

Если из дизъюнкции простых импликантов функции f нельзя отбросить ни одного слагаемого, то говорят, что получена тупиковая ДНФ (ТДНФ) функции f.

Тупиковая ДНФ функции f, содержащая минимальное число переменных или их отрицаний, называется минимальной ДНФ (МДНФ) функции f.