Вопросы для подготовки к зачёту
Понятия множества и элемента множества, примеры. Подмножество, собственное подмножество: определения, примеры. Способы задания множества.
Равные множества: определение, пример. Мощность конечного множества. Пустое множество: определение, пример.
Объединение и пересечение множеств, разность множеств, дополнение множества: определения и примеры.
Прямое (декартово) произведение множеств, его мощность.
Соответствие между множествами. Область определения и область значения соответствия.
Образ элемента при соответствии, прообраз элемента при соответствии: определения, примеры.
Взаимно однозначное соответствие: определения, пример.
Отображение множества в (на) множество.
Бинарное отношение на множестве. Свойства бинарного отношения: рефлексивность, симметричность, транзитивность.
Определения перестановок, размещений и сочетаний.
Бином Ньютона и простейшие свойства биномиальных коэффициентов.
Определение производящей функции последовательности. Определение линейного рекуррентного соотношения, описание его решения с помощью производящих функций.
Определение и описание чисел Фибоначчи.
Булевы функции и способы их задания. Существенная и фиктивная переменные.
Элементарные булевы функции. Основные эквивалентности.
Разложение функции по переменным. Совершенная дизъюнктивная нормальная форма.
Разложение функции по переменным. Совершенная конъюнктивная нормальная форма.
Полные системы. Примеры полных систем.
Теорема Жегалкина о представимости функции алгебры логики полиномом. Способы построения полиномов Жегалкина.
Понятие замкнутого класса. Замкнутость классов
,
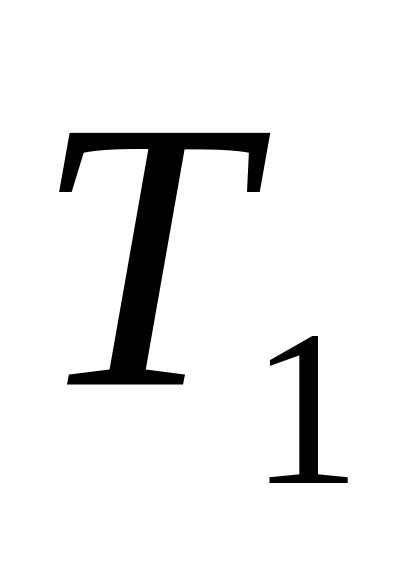и
.
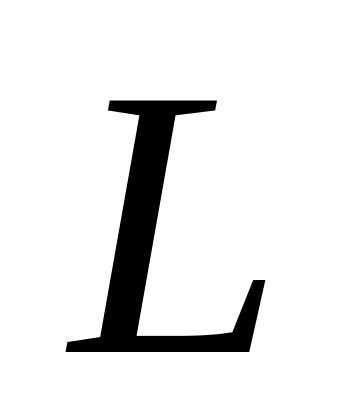Класс самодвойственных функций, его замкнутость.
Класс монотонных функций, его замкнутость.
Лемма о несамодвойственной функции.
Лемма о немонотонной функции.
Лемма о нелинейной функции.
Теорема Поста о полноте.
Теорема о максимальном числе функций в базисе алгебры логики.
Теорема о предполных классах.
Минимальная дизъюнктивная нормальная форма. Геометрическая интерпретация задачи минимизации булевых функций.
Сокращенная дизъюнктивная нормальная форма. Способы построения сокращенной дизъюнктивной нормальной формы
Геометрический способ построения сокращенной дизъюнктивной нормальной формы.
Метод Нильсона (построение сокращенной дизъюнктивной нормальной формы).
Метод Квайна (построение сокращенной дизъюнктивной нормальной формы).
Метод Блейка-Порецкого (построение сокращенной дизъюнктивной нормальной формы).
Определение графа. Вершины и рёбра. Графическая интерпретация графа.
Псевдограф, мультиграф, граф и их ориентированные аналоги.
Степень вершины графа.
Подграф. Путь, цепь, простая цепь, цикл, простой цикл.
Полный граф. Матрица смежности. Матрица инцидентности.
Связные графы. Компоненты связности графа, их число. Изоморфизм графов.
Двудольные графы.
Эйлеровы циклы. Эйлеровы графы. Критерий эйлеровости.
Гамильтоновы циклы. Гамильтоновы графы.
Деревья. Основные свойства деревьев.
Ориентированные (корневые) деревья. Лист. Ветвь. Высота ордерева. Уровень узла ордерева. Ярус дерева.
Упорядоченные деревья.
Бинарные деревья.
Укладка графа. Планарные графы. Плоские графы.
Теорема Эйлера и её следствия.
Непланарность графов К5 и К3,3.
Подразбиение графа. Гомеоморфизм графов. Теорема Понтрягина - Куратовского.