8. Полные метрические пространства. Сепарабельные пространства.

Последовательность называется сходящейся в себе (фундаментальной) в , если: для или .

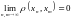Замечание: Любая сходящаяся последовательность является фундаментальной.

Метрическое пространство называется полным, если в нем всякая фундаментальная последовательность является сходящейся.

Множество называется всюду плотным в Х,

если любая точка есть предел последовательности элементов , то есть:

Иначе, Р всюду плотно в Х , если в любом шаре найдутся точки из Р. Очевидно, что

Пример: Множество рациональных чисел всюду плотно на числовой оси.

Метрическое пространство Х называется cепарабельным метрическим пространством, если в нем существует счетное всюду плотное множество.

Пример: Множество всех действительных чисел. Действительно, в нем счетным всюду плотным множеством является множество рациональных чисел.

Множество называется нигде не плотным в Х, если в шаре найдется другой шар

-18-

и не содержащий ни одной точки множества .

Пример: Множество натуральных чисел N нигде не плотное множество на числовой оси.

Точка множества , не являющаяся предельной

точкой этого множества, называется изолированной точкой М.

Если множество замкнуто и не содержит изолированных точек, то оно называется совершенным множеством.

Иначе говоря, для совершенного множества имеет место следующее равенство:

.

Примером совершенного множества может служить отрезок числовой оси или замкнутый шар евклидова пространства.

Упражнения 7:

1. Показать, что п- мерное евклидово пространство с расстоянием

является полным пространством.

1. Доказать, что пространство т - всех ограниченных числовых последовательностей - полное метрическое пространство.

3*.Доказать, что если - фундаментальная последовательность прост-

ранства М , то последовательность сходится для любого

элемента х пространства М.

4. Пусть - какое – либо ( полное или неполное) метрическое

-19-

пространство. Е его незамкнутое подмножество. Доказать, что Е неполное пространство.

5. Доказать, что подмножество полного метрического пространства полно тогда и только тогда, когда оно замкнуто в .

6. Доказать, что сумма конечного числа нигде не плотных множеств на числовой прямой является нигде не плотным множеством.

7.Какие из этих множеств являются совершенными:

а) ;

б) ;

в) ;

г) ;

д) - пустое множество;

е) - множество натуральных чисел;

8. Всегда ли пересечение двух совершенных множеств является совершенным множеством.

9. Доказать сепарабельность пространства .

9. Доказать сепарабельность пространства .

10. Пусть Р - всюду плотное множество на прямой. А - конечное подмножество множества Р. Доказать, что множество также всюду плотно на прямой.

12*.Существуют ли такие 2 всюду плотные несчетные множества на прямой, пересечение которых пусто ?

13*.Привести пример последовательности всюду плотных множеств 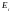на прямой таких, что , а их пересечение пусто, т.е. .