5. Метрические пространства.
Метрическим пространством называется произвольное множество М, в котором введено правило, позволяющее для любых двух элементов “х” и “у” из М построить неотрицательное число, называемое расстоянием от “ х ” до “ у ” и удовлетворяющее аксиомам расстояния ( метрики ):
1)
- аксиома
тождества,
-
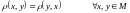аксиома
симметрии,
-
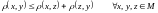аксиома
треугольника.
Примеры метрических пространств:
Множество п-мерных векторов
с
вещественными координатами и метрикой :
,
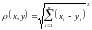Данное метрическое
пространство называют п
- мерным евклидовым пространством
.
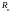Выполнение первых двух аксиом
очевидно, третью аксиому можно
доказать, воспользовавшись неравенством
Коши:
-11-
,
.
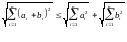2. Множество
непрерывных функций
,
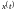где
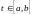с метрикой:
для всех
.
Это метрическое
пространство называется пространством
непрерывных функций, определенных
на отрезке
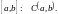
Точка
- некоторого произвольного
метрического пространства Х называется
пределом
последовательности
,
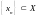если
,
Определенная таким образом сходимость называется сходимостью по метрике.
Сходимость в
евклидовом пространстве
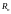по метрике есть сходимость по
координатам.
Сходимость в
пространстве
непрерывных функций по метрике
есть равномерная сходимость
последовательности функций на
[a,b].
Упражнения 5
Пусть М - множество, элементами которого являются всевозможные последовательности вещественных чисел
,
-12-
суммируемые
квадратом, т.е. такие, что
.
Расстояние между элементами
вычисляется по формуле:
.
Доказать, что множество М является метрическим пространством.
2. Пусть
т -
множество всех ограниченных
последовательностей вещественных
чисел
,
где
вообще зависящая от элемента х.
Расстояние между элементами
вычисляется по формуле:
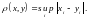
Доказать, что множество т является метрическим пространством.
3. Пусть
l
- множество, элементами которого
являются всевозможные последовательности
вещественных чисел
,
суммируемые по модулю, т.е.
Метрика
вычисляется по формуле:
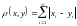
Доказать, что множество l является метрическим пространством.
Является ли метрическим пространством множество всех вещественных чисел, если под расстоянием между двумя числами подразумевать число
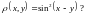
5. Является ли метрическим пространством множество всех подмножеств метрического пространства Х, если под расстоянием между двумя любыми подмножествами Е и F из Х подразумевать число
-13-
