
- •1.Основные понятия теории множеств
- •2. Операции над множествами
- •Симметрическая разность:
- •3. Счётные множества
- •Множества мощности континуума.
- •5. Метрические пространства.
- •6. Открытые множества.
- •7. Замкнутые множества. Замыкание.
- •8. Полные метрические пространства. Сепарабельные пространства.
- •9. Принцип сжатых отображений.
- •10. Компактные множества.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО ДИСЦИПЛИНЕ
«Функциональный анализ»
Практические занятия по курсу функционального анализа имеют целью содействовать лучшему усвоению студентами вводимых понятий и определений и овладению навыками самостоятельной работы.
На практических занятиях решаются задачи по следующим темам:
Занятие 1. Операции над множествами. Принцип двойственности.
Занятие 2. Счетные множества.
Занятие 3. Множества мощности континуума.
Задание 4. Метрические пространства.
Задание 5. Открытые множества.
Задание 6. Замкнутые множества.
Задание 7. Всюду плотные множества. Нигде не плотные множества.
Сепарабельные метрические пространства.
Задание 8. Полнота метрических пространств.
Задание 9. Принцип сжатых отображений.
Задание 10. Компактные множества.
ЛИТЕРАТУРА:
Люстерник Л.А., Соболев В.И. Элементы функционального анализа.
М.: Наука. 1965.
Люстерник Л.А., Соболев В.И. Краткий курс функционального анализа.
М.: Высшая школа, 1982.
Дополнительная:
1. Соболев В.И. Лекции по дополнительным главам математического
анализа. – М.: Наука, 1968.
-2-
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ:
Читается:
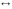 - взаимно -
однозначное соответствие;
- взаимно -
однозначное соответствие;
 - множество
- множество ;
;
 -
эквивалентно;
-
эквивалентно;
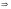 - следует;
- следует;
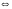 - тогда и
только тогда (необходимо и достаточно);
- тогда и
только тогда (необходимо и достаточно);
 - любой
(всякий, каждый);
- любой
(всякий, каждый);
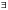 - существует
(найдется, по крайней мере );
- существует
(найдется, по крайней мере );
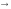 - стремится
к;
- стремится
к;
 - и ;
- и ;
 - или;
- или;
 - принадлежит;
- принадлежит;
 - не
принадлежит;
- не
принадлежит;
 - включено
( входит в, содержится в );
- включено
( входит в, содержится в );
 - включает
в себя ( содержит в себе );
- включает
в себя ( содержит в себе );
 -
пустое множество (мн-во, не содержащее
в себе элементов,
-
пустое множество (мн-во, не содержащее
в себе элементов,
например:
мн-во действительных корней уравнения
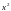 +1
= 0 );
+1
= 0 );
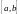 - отрезок ;
- отрезок ;
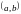 - интервал;
- интервал;
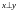 -
-
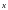 ортогонален
ортогонален
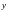 ;
;
 - множество
вещественных чисел;
- множество
вещественных чисел;
 - множество
рациональных чисел;
- множество
рациональных чисел;
 - множество
всех целых чисел;
- множество
всех целых чисел;
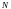 - множество
натуральных чисел;
- множество
натуральных чисел;
-3-
1.Основные понятия теории множеств
1.1 Множество - совокупность, собрание, ... (интуитивное понятие):
М
= { x:
.... }; M
= { x ....}
(.... - условие принадлежности
элемента х
к множеству М ).
....}
(.... - условие принадлежности
элемента х
к множеству М ).
1.2 Сравнение конечных множеств:
а) по количеству элементов;
б)
установлением
взаимно - однозначного соответствия
: (
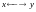 ).
).
1.3 Сравнение бесконечных множеств - по способу ( б ):
Пример: N = {n}, M = {2n} ( n = 1,2,.... ). N ~ M, так как n N 2n M
1.4 Мощность
множества
М:
 -
ТО ОБЩЕЕ,
что есть у всех множеств,
эквивалентных данному.
-
ТО ОБЩЕЕ,
что есть у всех множеств,
эквивалентных данному.
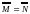 ,
так как
N~
M.
,
так как
N~
M.
Равенство множеств: если
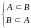 А
А
 В.
В.
Другими словами, множества равны, если они состоят из одних и тех же элементов.
1.6 Если А
В, но А В
А
,
то А - строгое
(собственное) подмножество
множества В.
В
А
,
то А - строгое
(собственное) подмножество
множества В.
Упражнения 1:
Сколько подмножеств имеет множество
 ,
состоящее из n
элементов.
,
состоящее из n
элементов.
Установить взаимно однозначное соответствие между поверхностью сферы с одной выколотой точкой и плоскостью.
3. Установить взаимно однозначное соответствие между отрезком прямой и всей прямой.
4. Установить
взаимно однозначное соответствие
между множествами
 и
и
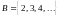 .
.
-4-
Установить взаимно однозначное соответствие между множеством всех натуральных чисел и множеством рациональных чисел отрезка
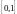
Доказать, что множество точек двух окружностей эквивалентны.
7. Доказать, что
если
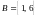 и А
есть множество корней
уравнения
и А
есть множество корней
уравнения
 ,
то
,
то
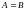 .
.
8. Доказать,
что
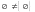 .
.
9*. Установить взаимно однозначное соответствие между множеством
точек
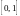 и
и
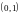 .
.
2. Операции над множествами
ОБЪЕДИНЕНИЕ МНОЖЕСТВ:
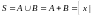
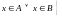 ;
;
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ:
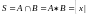
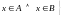 ;
;
РАЗНОСТЬ МНОЖЕСТВ:
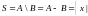
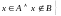 ;
;
Симметрическая разность:
Замечания:
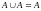 ;
;
 ;
;
если
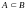 ,
то
,
то
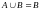 ,
а
,
а
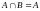 ;
;
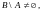 а
а
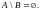
-5-
если
,
то
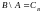
 - дополнение
мн-ва А
до мн-ва В;
- дополнение
мн-ва А
до мн-ва В;
если
 ,
то А и В - дизъюнктные
множества;
,
то А и В - дизъюнктные
множества;
в
общем случае
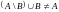 ,
а в частном, когда
,
а в частном, когда
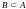 равенство
равенство
имеет место.
Упражнения 2:
 .
Чему равно
.
Чему равно
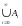 ?
?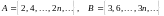 .
.
Чему равно
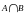 ? А\ В
?
? А\ В
?
3. А - множество
четных чисел натурального ряда. В -
множество натуральных чисел, делящихся
на 3, С - множество нечетных чисел,
не кратных 3.
Чему равно
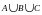 ?
?
4.Чему равны
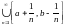 и
и
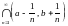 ?
?
Пусть
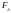 - множество точек плоскости, лежащих
на кривой
- множество точек плоскости, лежащих
на кривой
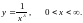 Чему равно множество
Чему равно множество
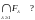
Существуют ли такие множества А, В и С , что
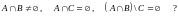
Доказать тождество:
а)
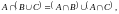
б)
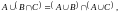
в)

г)
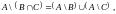
д)
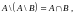
е)
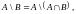
-6-
ж)
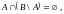
з)
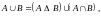
и)
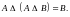
Определить операции
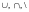 через
через
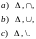
10*.Доказать, что
если множества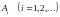 образуют убывающую последовательность,
т.е.
образуют убывающую последовательность,
т.е.
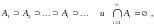
то

11*. Доказать, что
если множества
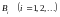 дизъюнктны
дизъюнктны
( т.е. попарно
не пересекаются ), а
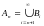 ,
то
,
то
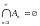 .
При этом очевидно, что множества
.
При этом очевидно, что множества
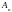 образуют
убывающую последовательность, т.е.
образуют
убывающую последовательность, т.е.
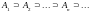 .
.
