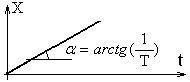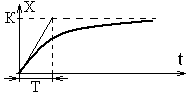1.5.2. Застосування перетворення Лапласа. Передавальна функція
Хай САР описується диференціальним рівнянням:
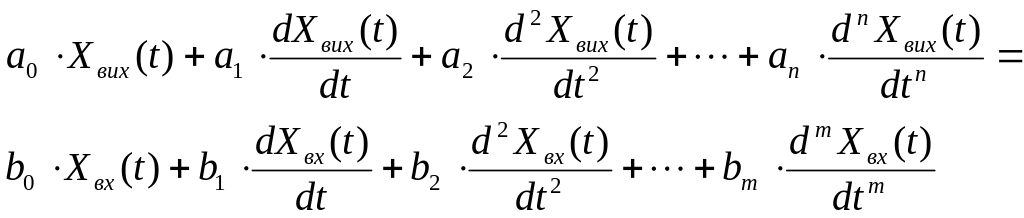(1.5.3)
причому n>m.
Перейдемо до зображень, скориставшись перетворенням Лапласа відповідно до п. 4 табл. 1.5.1:
(1.5.4)
Перетворимо, винісши за дужки Хвих(р) і Хвх(р) в лівій і правій частинах рівняння (1.5.4) відповідно:
(1.5.5)
Позначимо в рівнянні (1.5.5):
(1.5.6)
Тоді рівняння 1.5.1 можна записати у вигляді:
(1.5.7)
Виразимо з (1.5.7) відношення:
(1.5.8)
зване передавальною функцією. Передавальна функція однозначно визначає динамічні характеристики САР в цілому або окремих її ланок. Знаючи передавальну функцію будь-якого об'єкту, можна знайти зображення його вихідної величини
(1.5.9)
після чого можна знайти оригінал (тобто, функцію часу), провівши зворотне перетворення Лапласа.
Рівняння 
(1.5.10)
називається характеристичним, а його корені – полюсами передавальної функції.
Розглянемо для прикладу диференціальне рівняння (1.3.5), що описує нагрівальну піч:
Перейдемо до зображень:
Перетворимо:
,
Тоді передавальна функція печі визначиться виразом:
.
1.5.3. Типові ланки сар
При аналізі складної САР її структуру прийнято розбивати на окремі елементарні ланки. Елементарною називається ланка, що має один вхід і один вихід і що описується диференціальним рівнянням не вище за другий порядок. Зведемо опис типових елементарних ланок в таблицю 1.5.2. Пропорційна, інтегральна, диференціальна і аперіодична ланки були розглянуті раніше і не вимагають яких-небудь пояснень. Характеристичне рівняння коливальної ланки:
(1.5.11)
Корені цього рівняння
(1.5.12)
Залежно від значення величини , званої коефіцієнтом затухання, можливі 3 випадки:
А) >1 – обидва корені речовинні значення, що мають p1 і p2. Передавальна функція в цьому випадку може бути записана у вигляді:
- аперіодична ланка 2 порядку.
Б) 0<<1 – корені комплексні:
,
де
.
В цьому випадку перехідна характеристика описуватиметься виразом
(1.5.13)
і є затухаючими коливаннями.
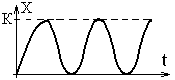
В) =0 – корені уявні:
- окремий випадок п. б), коли α
=
0. Відповідно до виразу (1.5.13) перехідна
характеристика буде незатухаючими
коливаннями.
1.5.4. З'єднання ланок. Передавальна функція замкнутої сар
В результаті розбиття САР на елементарні ланки в її структурі можуть з'явитися ділянки з послідовним і паралельним з'єднанням. Правила об'єднання таких ділянок наступні:
А) Послідовне з'єднання:
W1(p)
W2(p)
X
ВХ(р) XВИХ(р)
В цьому випадку передавальна функція еквівалентної ланки буде дорівнюватись добутку передавальних функцій ланок, що входять в ділянку з послідовним з'єднанням:
Wпосл(p) = W1(p) W2(p) (1.5.14)
Б) Паралельне з'єднання:
Таблиця 1.5.2. Типові елементарні ланки САР
Тип ланки |
Математичний опис |
Передавальна функція |
Перехідна характеристика |
|
Пропорційна |
|
|
|
|
Інтегруюча |
|
|
|
|
Диференційна |
|
|
Імпульс
|
|
Аперіодична |
|
|
|
|
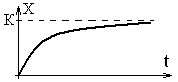
Коливальна |
|
|
|
>1
0<<1
=0 |
або
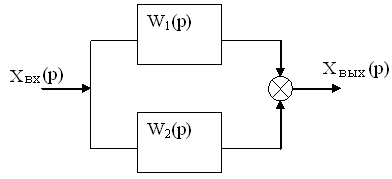
При такому з'єднанні еквівалентна передавальна функція буде дорівнюватись сумі передавальних функцій:
Wпар(p) = W1(p) + W2(p) (1.5.15)
В результаті перетворень шляхом заміни ділянок з послідовним і паралельним з'єднанням еквівалентними структурна схема САР прийме вигляд:
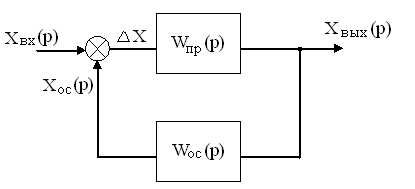
де Wпр(p) – передавальна функція прямої частини САР;
Wзз(p) – передавальна функція каналу зворотного зв'язку.
Можна показати, що передавальна функція замкненої САР визначиться виразом:
(1.5.16)
де Wроз(p) = Wпр(p) Wзз(p) – передавальна функція розімкненої системи.