Линейная алгоритмическая структура

Линейный (последовательный) алгоритм - это последовательность действий, выполняемых однократно в заданном порядке. Для примера составим алгоритм вычисления следующего выражения: (75-40)-(22+10).

1. Вычислить разность 75 и 40.

2. Сложить числа 22 и 10.

3. Вычислить разность результатов 1-го и 2-го действий.

Действия в этом алгоритме выполняются в том порядке, в котором записаны. Из записи алгоритма видно, что при его исполнении получаются два про­межуточных результата - в 1-м и 2-м действии. Для того, чтобы их зафиксировать, выделяется специальная область памяти, которую называют переменной. В отличие от математики, в программировании значения переменных могут многократно изменяться по ходу вычислений. Кроме этого переменные могут использоваться для хранения совершенно различных типов данных - не обязательно числовых.

Пример: блок-схема линейного алгоритма для вычисления (75 - 40) - (22+10)(см. рис).

Пример программы

на языке Паскаль

Program Z1;

var A,B,S:real;

begin

A:=75-40;

B:=22+10;

S:=A-B;

Write(‘S=’,S);

end.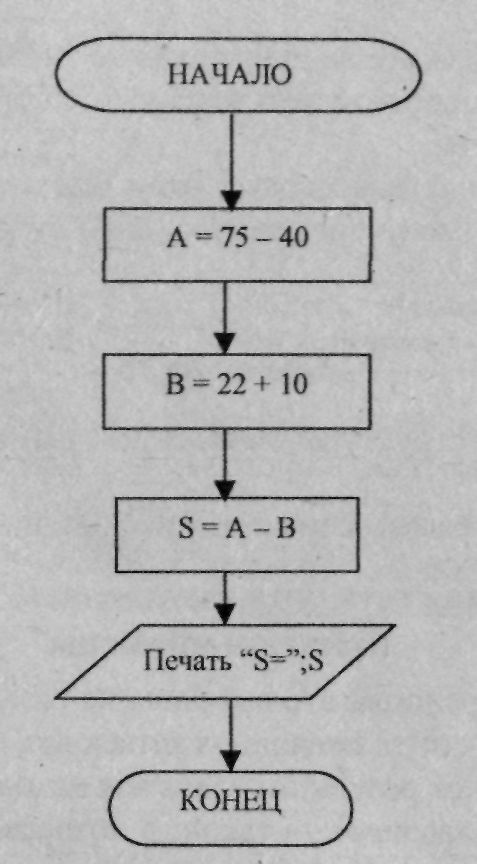

Рис. Линейная алгоритмическая структура

Билет 9

1. Логические величины, операции, выражения. Логические выражения в качестве условий в ветвящихся и циклических алгоритмах.

Логика - это наука о формах и способах мышления. Основоположником формальной логики является Аристотель, который впервые отделил логические формы мышления от его содержания.

Мышление всегда осуществляется в каких-то формах. Выделяют три основные: понятие, высказывание и умозаключение.

Высказывание - это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо отрицается или утверждается.

По поводу высказывание можно сказать, истинно оно или ложно. Истинным будет высказывание, в котором связь понятий правильно отражает свойства отношения реальных вещей. Ложным высказывание будет, если оно противоречит реальной действительности.

Пример: "Буква а - гласная". (это истинное высказывание).

Алгебра логики

Алгебра - это наука об общих операциях, аналогичных сложению и умножению, которые выполняются не только над числами, но и над другими математическими объектами, в том числе и над высказываниями. Такая алгебра называется алгеброй логики. Алгебра принимает во внимание только истинность или ложность высказывания.

Логическая переменная - это простое высказывание, содержащее только одну мысль. Ее символическое обозначение - латинская буква (например, A, B,C,F). Значением логической переменной могут быть только константы ИСТИНА (1) и ЛОЖЬ (0).

Составное высказывание - логическая функция, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение - F.

На основании простых высказываний могут быть построены составные высказывания.

Базовые логические операции:

1. Логическое умножение (конъюнкция) (соответствует союз "И")

Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

А	В	F = A /\ B
0	0	0
0	1	0
1	0	0
1	1	1

2. Логическое сложение (дизъюнкция) (соответствует союз "ИЛИ")

Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

А	В	F = A \/ B
0	0	0
0	1	1
1	0	1
1	1	1

3. Логическое отрицание (инверсия) (соответствует частица "НЕ")

Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным

А	F = A
0	1
1	0