1. Определение сопротивлений.

Реактивные сопротивления элементов L и С находим по формулам:

(2.8)

X_L = ωL, X_C = 1 / ωC, ω = 2πf.

Полное сопротивление цепи равно:

(2.9)

,

угол сдвига фаз равен:

(2.10)

φ = arctg((X_L - X_C) / R).

2. Нахождение тока. Ток в цепи находится по закону Ома

I = U / Z, ψ_i = ψ_u + φ.

Фазы тока и напряжения отличаются на угол φ.

3. Расчет напряжений на элементах.

Напряжения на элементах определяются по формулам:

(2.11)

U_R = I R, ψ_uR = ψ_i ;

(2.12)

U_L = I X_L, ψ_uL = ψ_i + 90°;

(2.13)

U_C = I X_C, ψ_uC = ψ_i - 90°.

Для напряжений выполняется второй закон Кирхгофа в векторной форме:

(2.14)

Ú = Ú_R + Ú_L + Ú_C.

4. Анализ расчетных данных. В зависимости от величин L и С в формуле (2.8) возможны следующие варианты: X_L > X_C; X_L < X_C; X_L = X_C.

Для варианта X_L > X_C угол φ > 0, U_L > U_C. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид (рис. 31).

Рис. 31 Векторная диаграмма напряжений

Для варианта X_L < X_C угол φ < 0, U_L < U_C. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид (рис. 32).

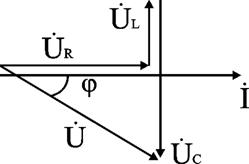
Рис. 32 Векторная диаграмма напряжений

Для варианта X_L = X_C угол φ = 0, U_L = U_C. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление z=R наименьшее из всех возможных значений X_L и X_C. Векторная диаграмма напряжений имеет вид (рис. 33).

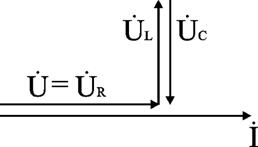
Рис. 33 Векторная диаграмма напряжений

Этот режим называется резонанс напряжений (U_L = U_C). Напряжения на элементах U_L и U_C могут значительно превышать входное напряжение.

Пример:

U = 220 B, f = 50 Гц, R = 22 Ом, L =  350 мГн, С =  28,9 мкФ.

X_L = ωL = 2πf L = 2 · 3,14 · 50 · 0,35 = 110 Ом; X_C = 1 / ωC = 1 / (2πf C) = 110 Ом; Z = R = 22 Ом, φ=0, I = U / R = 220 / 22 = 10 А, ψ_u = ψ_i; U_L = U_C = I X_L = 10 · 110 = 1100 В.

В приведенном примере U_L и U_С превышают входное напряжение в 5 раз.

5.5. Цепь с параллельным соединением элементов

Проведем анализ работы электрической цепи с параллельным соединением элементов R, L, С. Рассмотрим следующую схему (рис. 34).

Рис. 34 Цепь с параллельным соединением элементов

Предположим, что заданы величины R₁, R₂, L, С, частота f и входное напряжение U. Требуется определить токи в ветвях и ток всей цепи.

В данной схеме две ветви. Согласно свойству параллельного соединения, напряжение на всех ветвях параллельной цепи одинаковое, если пренебречь сопротивлением подводящих проводов. Задача разбивается на ряд этапов.

1. Определение сопротивлений ветвей.

Реактивные сопротивления элементов L и С определяем по формулам:

(2.15)

X_L = ωL, X_C = 1 / ωC, ω = 2πf.

Полное сопротивление ветвей равны:

(2.16)

, ,

соответствующие им углы сдвига фаз:

(2.17)

φ₁ = arctg(X_L / R₁), φ₂ = arctg(X_С / R₂).

2. Нахождение токов в ветвях.

Токи в ветвях находятся по закону Ома:

I₁ = U / Z₁, ψ_i1 = ψ_u + φ₁, I₂ = U / Z₂, ψ_i2 = ψ_u + φ₂.

3. Нахождение тока всей цепи.

Ток всей цепи может быть найден несколькими методами: графическим, методом мощностей, методом проекций и методом проводимостей.

Чаще всего используют метод проекций и метод проводимостей. В методе проекций ток I₁ и I₂ раскладываются по две ортогональные составляющие активную и реактивную. Ось активной составляющей совпадает с вектором напряжения U. Ось реактивной составляющей перпендикулярна вектору U (рис. 35).

Рис. 35 Ось реактивной составляющей

Активные составляющие токов равны:

(2.18)

I_1а = I₁ cos φ₁, I_2а = I₂ cos φ₂,

(2.19)

I_а = I_1а + I_2а.

Реактивные составляющие токов равны:

(2.20)

I_1р = I₁ sin φ₁, I_2р = I₂ sin φ₂,

(2.21)

I_р = I_1р - I_2р.

В последнем уравнении взят знак минус, поскольку составляющие I_1р (индуктивная) и I_2р (емкостная) направлены в разные стороны от оси U.

Полный ток находится из уравнений:

(2.22)

,

(2.23)

φ = arctg(I_р / I_а).

В методе проводимостей также используется разложение на активные и реактивные составляющие. Активные составляющие токов записываются в виде:

(2.24)

,

где через g₁ = R₁ / Z₁² обозначена величина названная активной проводимостью первой ветви. Аналогичным образом получим:

(2.25)

,

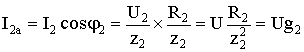где g₂ = R₂ / Z₂²; а величину g = g₁ + g₂ называют активной проводимостью всей цепи.

Запишем реактивные составляющие токов:

(2.26)

,

(2.27)

,

где b₁ и b₂ – реактивные проводимости ветвей b₁ = X_L / Z₁², b₂ = X_C / Z₂². Для реактивной проводимости всей цепи имеем:

(2.28)

b = b₁ - b₂.