Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Новгородский государственный университет имени Ярослава Мудрого»
Великий Новгород
Институт электронных и информационных систем
К
афедра
прикладной математики и информатики
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ
«Эконометрика»
Выполнила:
студентка группы 9311
__________Е. В. Зарубина
“ ___”_____________2013 г.
Проверил:
________Н. В. Рутковский
“ ___”_____________2013 г.
Задача 1.
Рассмотрим набор наблюдений:
х |
9.0 |
9.6 |
9.8 |
10.3 |
10.2 |
10.6 |
11.1 |
11.0 |
11.3 |
11.7 |
у |
15.2 |
16.4 |
16.7 |
16.9 |
16.9 |
17.2 |
17.8 |
1.57 |
17.9 |
18.1 |
Постройте две регрессии:
По модели у от х
Получится уравнение :
б) по модели х от у
Получится уравнение :
Нарисуйте на координатной плоскости обе линии. Совпадают ли они? Почему? Чтобы понять, почему возникает расхождение, установите при каких условиях линии совпадать.
Решение.
№ |
x |
у |
х2 |
у2 |
ху |
1 |
9.0 |
15.2 |
81.00 |
231.04 |
136.80 |
2 |
9.6 |
16.4 |
92.16 |
268.96 |
157.44 |
3 |
9.8 |
16.7 |
96.04 |
278.89 |
163.66 |
4 |
10.3 |
16.9 |
106.09 |
285.61 |
174.07 |
5 |
10.2 |
16.9 |
104.04 |
285.61 |
172.38 |
6 |
10.6 |
17.2 |
112.36 |
295.84 |
182.32 |
7 |
11.1 |
17.8 |
123.21 |
316.84 |
197.58 |
8 |
11.0 |
17.5 |
121.00 |
306.25 |
192.50 |
9 |
11.3 |
17.9 |
127.69 |
320.41 |
202.27 |
10 |
11.7 |
18.1 |
136.89 |
327.61 |
211.77 |
средн. |
10.46 |
17.06 |
110.048 |
291.706 |
179.079 |
𝜎2 |
0.6364 |
0.6624 |
|
|
|
𝜎 |
0.7978 |
0.8139 |
|
|
|
а)
б)
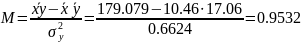
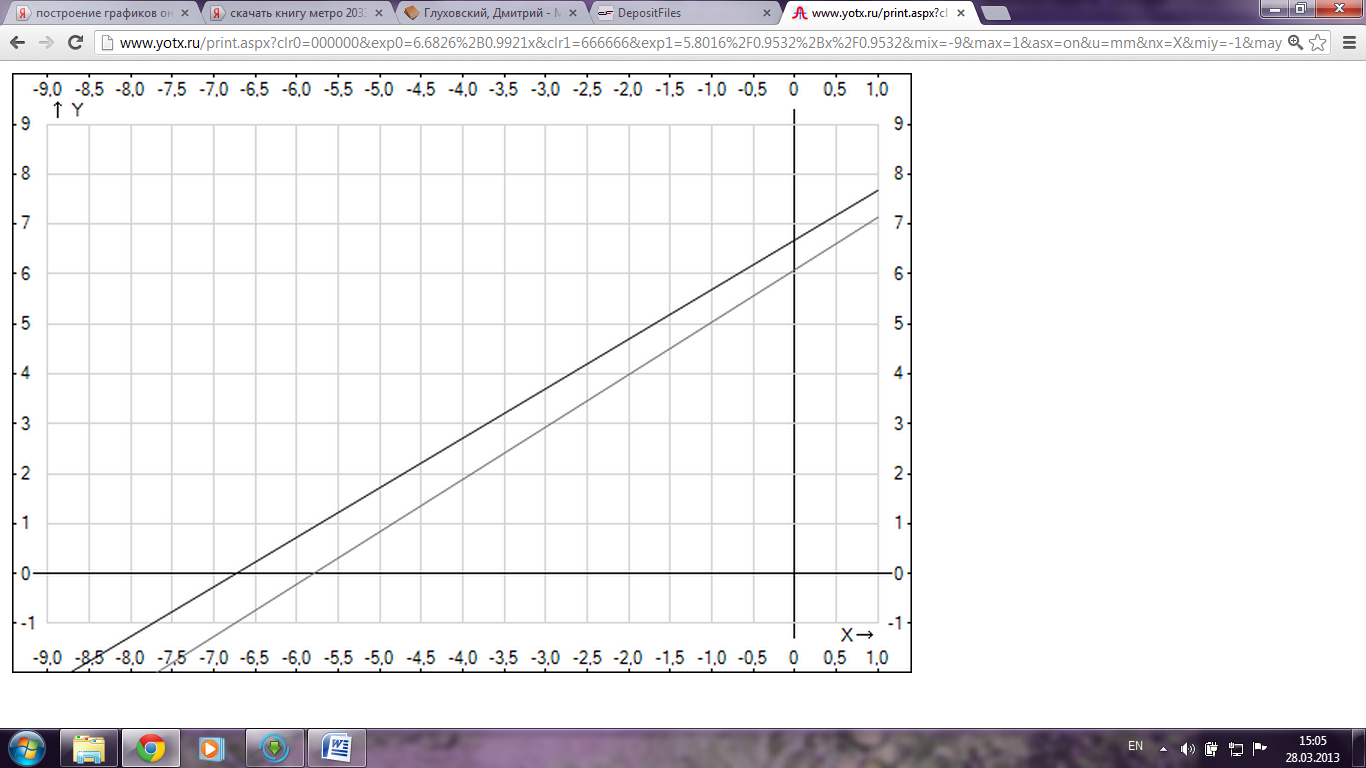
На графике видно, что прямые не совпадают. Определим условия, при которых прямые будут совпадать.
Получаем условие на корреляцию:
.
Задача 2.
В таблице представлены результаты наблюдений за двумя переменными:
у- сумма, потраченная населением страны на потребление за год и
х- доходы населения за этот год
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
у |
69.0 |
69.8 |
70.6 |
71.4 |
72.4 |
70.2 |
71.1 |
х |
103.6 |
102.2 |
100.1 |
97.8 |
95.9 |
96.4 |
97.3 |
Найдите
уравнение простой регрессии
и стандартные ошибки коэффициентов.
Проверьте значимость регрессии с помощью
t-статистики
Стьюдента (5%) для коэффициента В.
Сформулируйте математически и проверьте
гипотезу
Н0: рост доходов на 1 млрд. вызывает увеличение потребления на 1 млрд.
Решение.
№ |
x |
у |
х2 |
у2 |
ху |
1 |
103.6 |
69.0 |
10732.96 |
4761.00 |
7148.40 |
2 |
102.2 |
69.8 |
10444.84 |
4872.04 |
7133.56 |
3 |
100.1 |
70.6 |
10020.01 |
4984.36 |
7067.06 |
4 |
97.8 |
71.4 |
9564.84 |
5097.96 |
6982.92 |
5 |
95.9 |
72.4 |
9196.81 |
5241.76 |
6943.16 |
6 |
96.4 |
70.2 |
9292.96 |
4928.04 |
6767.28 |
7 |
97.3 |
71.1 |
9467.29 |
5055.21 |
6918.03 |
средн. |
99.04 |
70.64 |
9817.10 |
4991.48 |
6994.34 |
𝜎2 |
8.18 |
1.47 |
|
|
|
𝜎 |
2.86 |
1.21 |
|
|
|
Получаем уравнение регрессии:
Проверьте значимость регрессии:
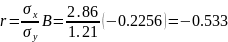
При
уровне значимости
При
уровне значимости
уравнение
незначимо.
Найдем стандартные ошибки коэффициентов и проверим значимость коэффициентов уравнения регрессии:
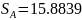
При
доверительной вероятности
коэффициент
А значим
коэффициент
В незначим
Проверим гипотезу
Н0: рост доходов на 1 млрд. вызывает увеличение потребления на 1 млрд.
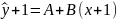
Н0:
Но
по подсчетам
.
Таким образом гипотеза Н0
не
верна:
рост доходов на 1 млрд. не вызывает увеличение потребления на 1 млрд.
Задача 3.
Две
студентки 2 курса экономического
факультета вычисляют одну и ту же
величину А. Из-за неточности вычислений
они получают два различных ответа:
Будем условно считать, что
– независимые случайные величины с
математическим ожиданием
.
Первая студентка утверждает, что
допускает при вычислениях дисперсию
,
а вторая-
.
Сделайте на основе этих данных наилучшую
линейную оценку величины А.
Решение.
Наилучшая линейная оценка величины А:
где
x, y - неизвестные коэффициенты, которые
будем искать из условия задачи:
,
.
Оценка величины А должна быть несмещённой,
то есть
,
и эффективной в данном классе несмещённых
оценок, то есть
.
Так как - независимые случайные величины, то
Пусть
т.е.
В
итоге получаем, что
является наилучшей линейной оценкой
А.
Задача 4.
Продавец журналов хочет выявить оптимальную цену на журнал “Рыболов” и поэтому в течение 3 месяцев проводит опыты- меняет цены и записывает количество проданных журналов. Данные- в таблице:
№ |
p |
q |
№ |
p |
q |
1 |
35.0 |
142 |
7 |
33.5 |
153 |
2 |
35.5 |
130 |
8 |
34 |
140 |
3 |
34 |
145 |
9 |
36.5 |
127 |
4 |
36 |
132 |
10 |
40 |
93 |
5 |
35.5 |
134 |
11 |
39 |
108 |
6 |
37 |
124 |
12 |
38 |
115 |
Оцените
парную регрессию
и логарифмическую регрессию
.
Найдите оптимальную цену (в смысле
максимума выручки)
в первом и втором случае. Какую цену выберете вы ?