Основные представления теории Бора.

е  = 1,6×10^-19 Кл, ₀ = 8,8510^-12 Ф/м

Линейчатые спектры

Формула Ридберга – Бальмера, описывающая серии в спектре атома водорода и водородоподобных ионов (He⁺ и Li⁺⁺ и т.д.)

,

где  – частота спектральных линий, R = 1,09710⁷ м^-1 – постоянная Ридберга, с = 310⁸ м/с – скорость света в вакууме, n и m – целые числа. n определяет серию (n = 1, 2, 3, …), m определяет отдельные линии в серии (m = n +1, n +2, n +3, …).

n  = 1 – серия Лаймана (УФ),

n = 2 – серия Бальмера (УФ, В),

n = 3 – серия Пашена (ИК),

n = 4 – серия Брэкета (ИК),

n = 5 – серия Пфунда (ИК),

n = 6 – серия Хэмфри (ИК).

Каждая серия имеет границу, соответствующую m = . Это наибольшая частота серии или наименьшая длина волны  .

, где U – разность потенциалов

, U_I – первый потенциал возбуждения

, U_II – второй потенциал возбуждения

, U_i –потенциал ионизации, – энергия ионизации

Волны де Бройля.

; если v  с, если v  с, , .

где h = 6,6210^-34 Джс – постоянная Планка, р – импульс, m – масса частицы, W_k – кинетическая энергия, U – ускоряющая разность потенциалов, q– заряд, с = 310⁸ м/с – скорость света в вакууме, v – скорость движения,. Для электрона q = е = 1,6×10^-19 Кл, m = m_е = 9,110^-31 кг.

С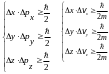 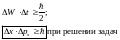оотношение неопределенностей

г де  = 1,0510^-34 Джс,

x– неопределенность координаты, р_x – неопределенность проекции импульса на ось x, v_x – неопределенность проекции скорости на ось x, р_x– проекция импульса на ось x, v_x – проекция скорости на ось x, m – масса, W – неопределенность энергии частицы в каком–либо состоянии, t – время пребывания частицы в этом состоянии.

Уравнение Шредингера

– уравнение Шредингера для стационарных состояний.  = f(x, y, z) – волновая функция, U(x, y, z) – потенциальная энергия, W – полная энергия, m – масса частицы,  = 1,0510^-34 Джс– постоянная Дирака

Ч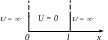 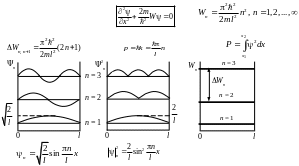астица в одномерной прямоугольной бесконечно глубокой «потенциальной яме»

где W_n – собственные значения энергии, l – ширина ямы, n – квантовое число, W_n – энергетическая разность между уровнями, p –импульс частицы, k – волновое число, P – вероятность нахождения частицы в интервале от x₁ до x₂, _n – волновая функция , ||²_n – плотность вероятности.

Сложные (многоэлектронные) атомы

n = 1, 2, …, ¥ – главное квантовое число

l = 0, 1, 2, …, (n-1) – азимутальное (орбитальное) квантовое число

m = 0, ±1, ±2, …,± l - магнитное квантовое число

m_s = 1/2 - магнитное спиновое квантовое число

	Слой	Число электронов в состояниях					Макси­мальное число электро­нов
		s (l = 0)	p (l = 1)	d (l = 2)	f (l = 3)	g (l = 4)
1	K	2	-	-	-	-	2
2	L	2	6	-	-	-	8
3	M	2	6	10	-	-	18
4	N	2	6	10	14	-	32
5	O	2	6	10	14	18	50

АТОМ
– собственные значения энергии n = 1, 2, …,  – главное квантовое число
– момент импульса			– магнитный момент
l = 0, 1, 2, …, (n -1) – орбитальное (азимутальное) квантовое число
– проекция момента импульса на направление внешнего магнитного поля				– проекция магнитного момента на направление внешнего магнитного поля
m = 0, 1, 2, …,  l – магнитное квантовое число
– собственный момент импульса		– спиновое квантовое число			собственный магнитный момент
– проекция собственного момента импульса на направление внешнего магнитного поля		– магнитное спиновое квантовое число			– проекция собственного магнитного момента на направление внешнего магнитного поля
= 0,92710-23 Дж/Тл– магнетон Бора