Э лектромагнитные незатухающие колебания

• Дифференциальное уравнение гармонических электромагнитных свободных незатухающих колебаний

, его решение q = q_mcos(₀t + ₀), q – заряд на обкладках конденсатора, – собственная частота колебаний, – период колебаний (формула Томсона). L – индуктивность катушки, C – емкость конденсатора.

U = U_mcos(₀ t + ₀) – напряжение на конденсаторе, U_m = q_m/C,

I = –I_msin(₀t + ₀) – сила тока в контуре, I_m = q_m.

Энергия электрического поля W_эл, магнитного W_магн и полная W определяются соотношениями:

–

закон сохранения полной энергии в колебательном контуре.

• Электромагнитные затухающие и вынужденные колебания

• В 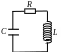контуре, содержащем емкость (C), индуктивность (L) и сопротивление (R) свободные электромагнитные колебания будут затухающими из-за выделения теплоты на сопротивлении.

Дифференциальное уравнение свободных затухающих колебаний – (1), где –коэффициент затухания.

– решение (1).

, .

• Амплитудные значения заряда конденсатора, напряжения на его обкладках и силы тока, а также энергия в цепи со временем будут убывать по экспоненциальному закону:

, , .

• Если в колебательный контур включить источник, напряжение на котором изменяется по гармоническому закону 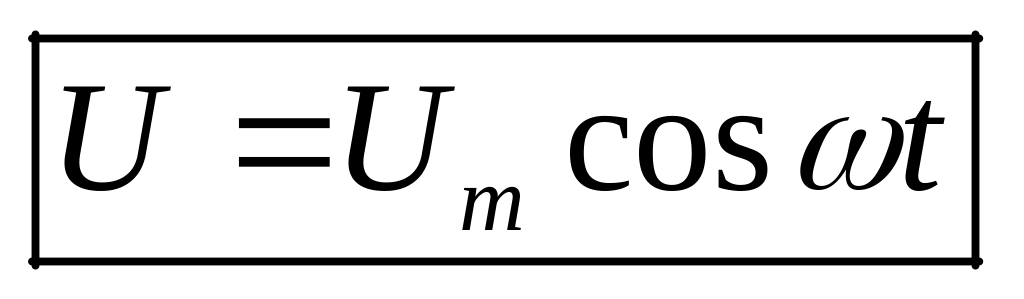, в контуре возникнут вынужденные незатухающие колебания заряда, напряжения и силы тока с частотой вынуждающего напряжения .

• Установившиеся вынужденные электромагнитные колебания в контуре называют переменным током. В последовательной LRC –цепи переменного тока сила тока во всех участках цепи в каждый момент времени одинакова, а сумма мгновенных напряжений U_R, U_L, U_C равна значению приложенного напряжения U в тот же момент времени: U = U_R+U_L+U_C.

• приложенное на источнике напряжение U, сила тока в контуре I и напряжение на отдельных элементах цепи изменяются по закону:

• , , , , .

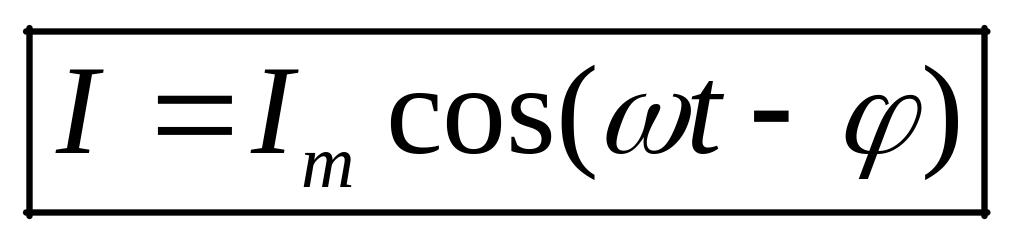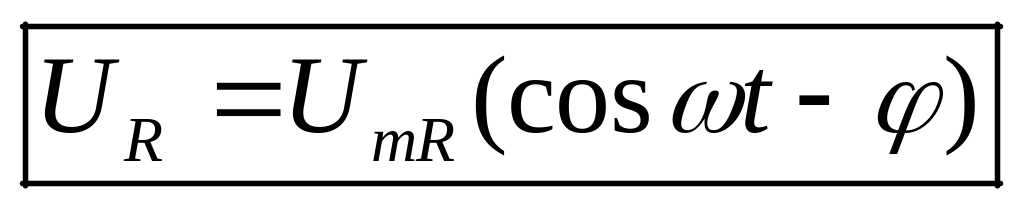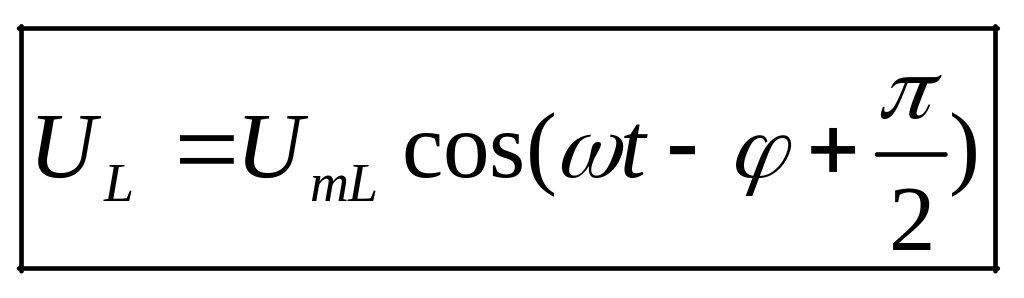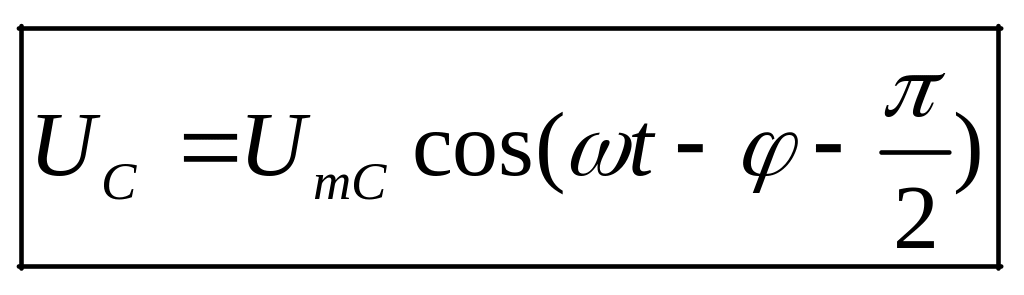• С 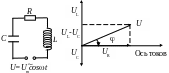оотношения между токами и напряжениями на различных элементах удобно находить с помощью векторных диаграмм. Каждой величине, меняющейся по синусоидальному закону, сопоставляется вектор, длина которого равна амплитудному значению соответствующей величины, а углы между различными векторами равны фазовым сдвигам между соответствующими величинами.

• Из векторной диаграммы находятся величины I_m и :

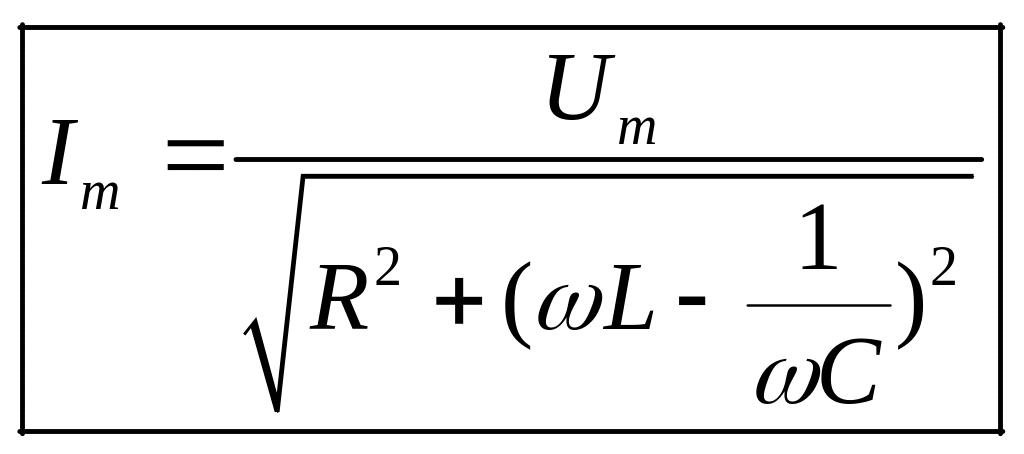
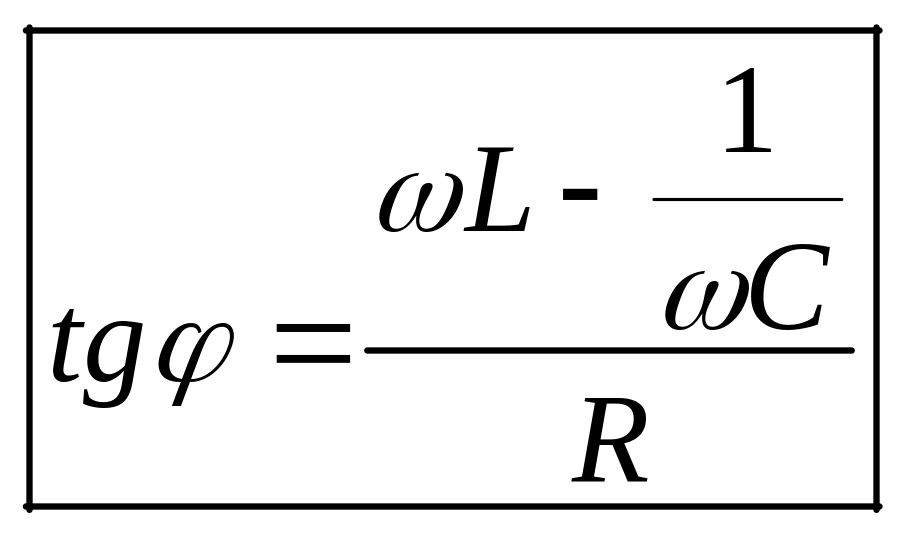, . Связь между амплитудным значением тока и амплитудными значениями напряжений на отдельных элементах цепи: , , .

При w = w₀ – наблюдается явление резонанса напряжений: U_L = U_C, а сила тока в контуре достигает максимального значения .

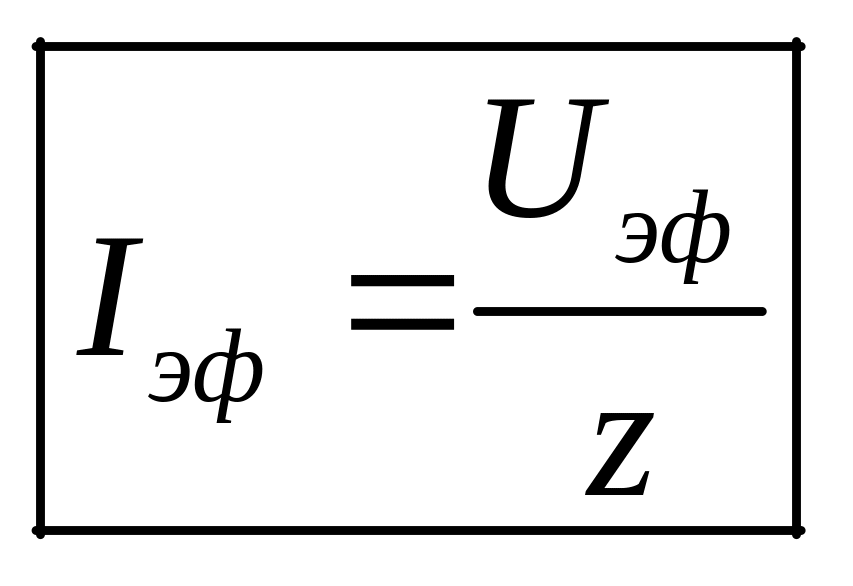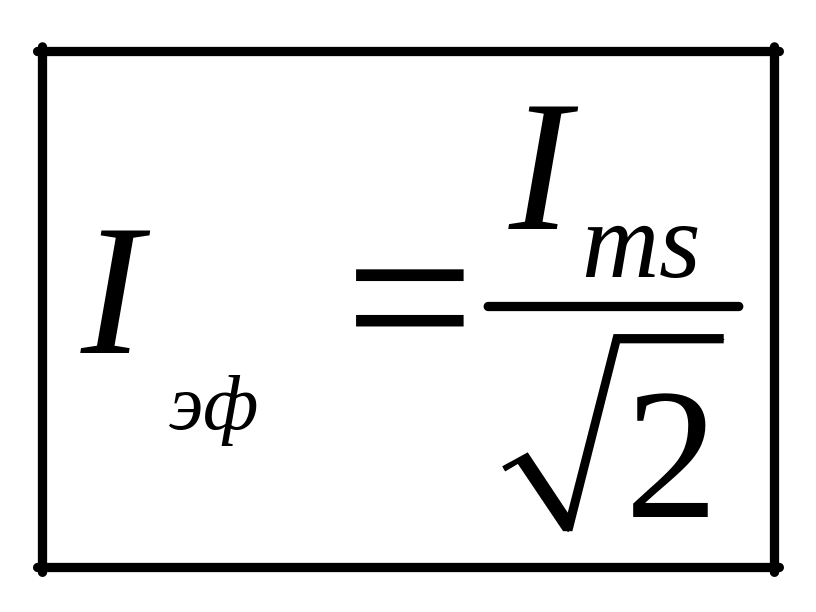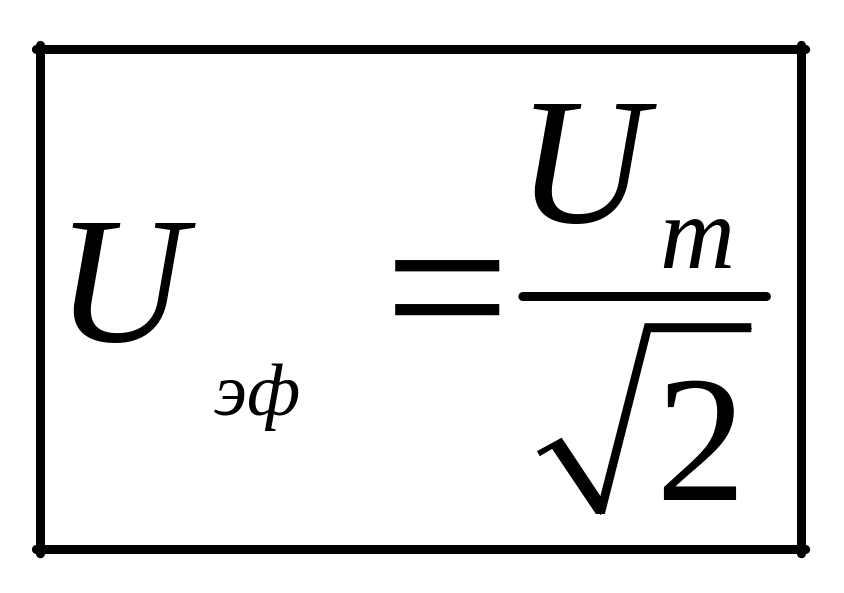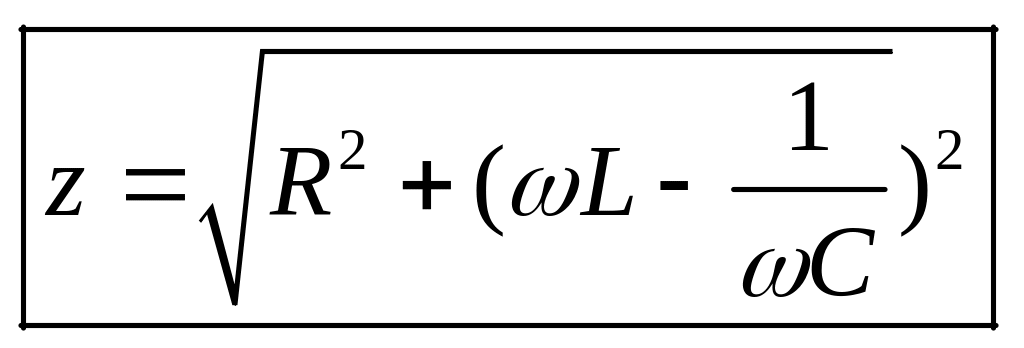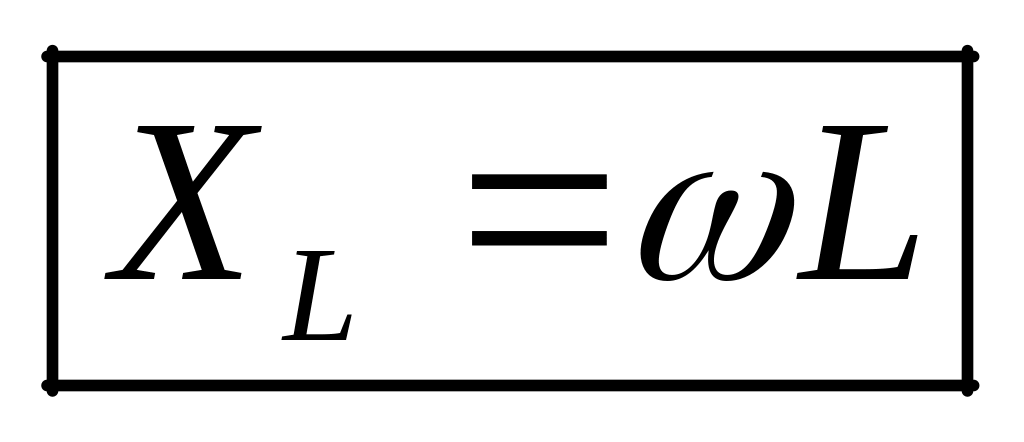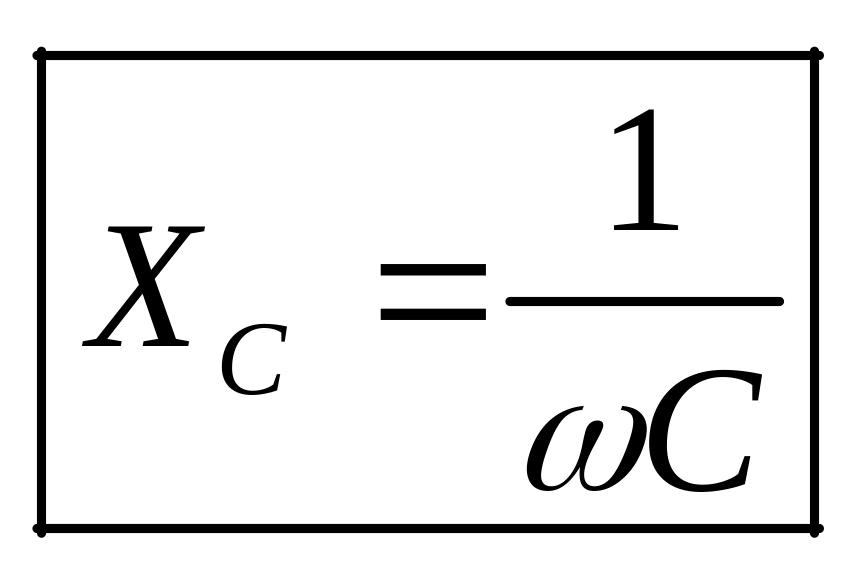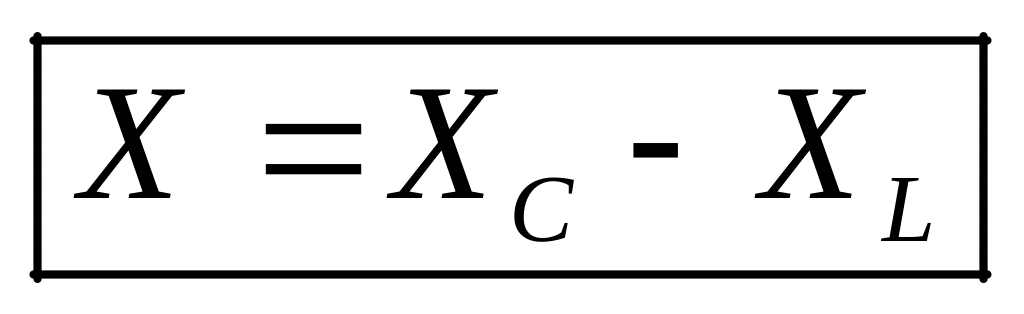• Соотношение формально похоже на закон Ома. Для переменного тока закон Ома записывают в виде: , где , . Величину называют полным сопротивлением цепи переменному току или импедансом, – индуктивным сопротивлением, – емкостным сопротивлением, (36) – реактивным сопротивлением.

Мощность переменного тока .

• Электромагнитные (э/м) волны

= cos(t –kx+ ₀)

= cos(t –kx+ ₀)

– уравнение плоской бегущей э/м волны, где E – напряженность электрического поля, [E] = 1 В/м, H – напряженность магнитного поля, [H] = 1 А/м.

. – закон Максвелла, определяет скорость распространения э/м волны в среде с диэлектрической проницаемостью среды  и магнитной проницаемостью среды . , где – показатель преломления среды. с = 310⁸ м/с, ₀ = 8,85×10^–12 ф/м, ₀ = 4×10^–7 гн/м.   1 для всех сред, кроме ферромагнетиков.

• При переходе их одной среды в другую  = const, 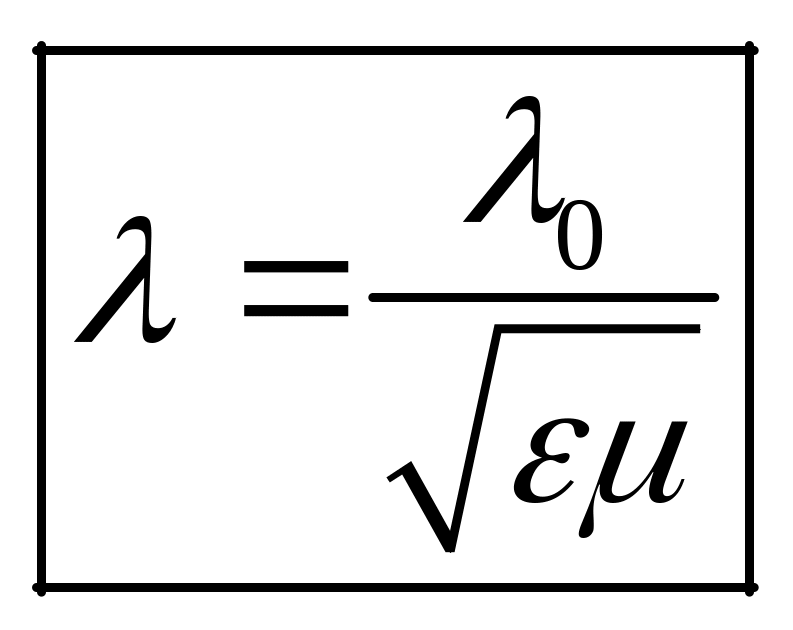, где ₀ – длина волны в вакууме (воздухе). .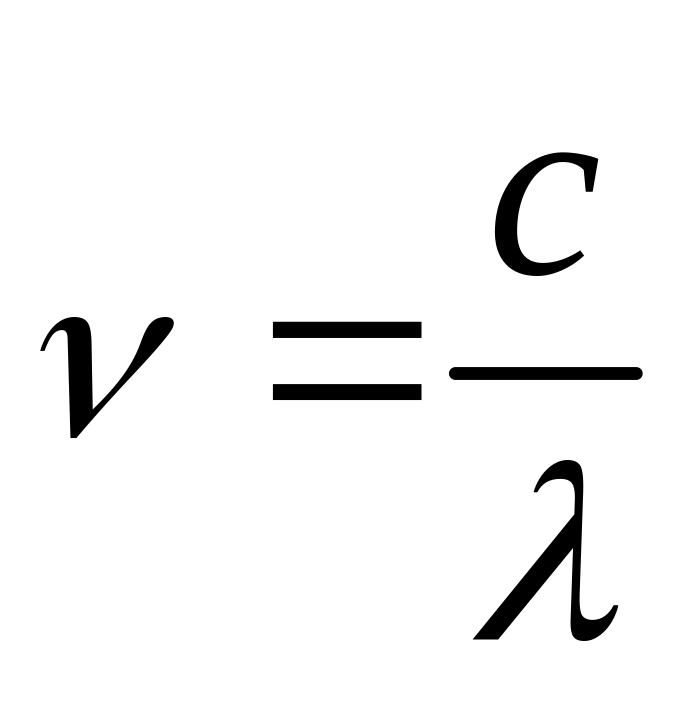

Шкала электромагнитных волн

Вид излучения	Радио волны	Световые волны			Рентгеновское излучение	– излучение
		ИК	Видимый свет	УФ
, м	103 – 10–4	510–4– 7,610–7	7,610–7– 410–7	410–7– 10–9	210–9 – 610–12	 610–12
, Гц	3105 – 31012	61011– 3,91014	3,91014– 7,51014	7,51014– 31017	1,51017 – 51019	51019

оптика

• Видимый свет – это э/м волны длиной от 0,4 мкм до 0,76 мкм или  = (0,39 0,75)10¹⁵ Гц. Невидимый свет с   0,76 мкм называют инфракрасным (ИК), с  0,4 мкм – ультрафиолетовым (УФ).

• условное деление оптического излучения на поддиапазоны.

Поддиапазоны	Границы поддиапазонов , мкм
Вакуумная УФ область	0,010 – 0,185
Ближняя УФ область	0,185 – 0,380
Видимый свет:	0,380 – 0,760
фиолетовый	0,380 – 0,45
синий	0,45 – 0,48
голубой	0,48 – 0,51
зеленый	0,51 – 0,55
желто-зеленый	0,55 – 0,575
желтый	0,575 – 0,59
оранжевый	0,59 – 0,62
красный	0,62 – 0,76
Ближняя ИК область	0,76 – 3,0
Средняя ИК область	3,0 – 50
Дальняя ИК область	50 - 1000

• Оптика делится на геометрическую, волновую и квантовую.

• Геометрическая оптика – использует представление о световых лучах – направлениях, вдоль которых происходит перенос энергии световых колебаний.

• Оптические свойства прозрачной среды характеризуются абсолютным показателем преломления, определяющим фазовую скорость световых волн: . 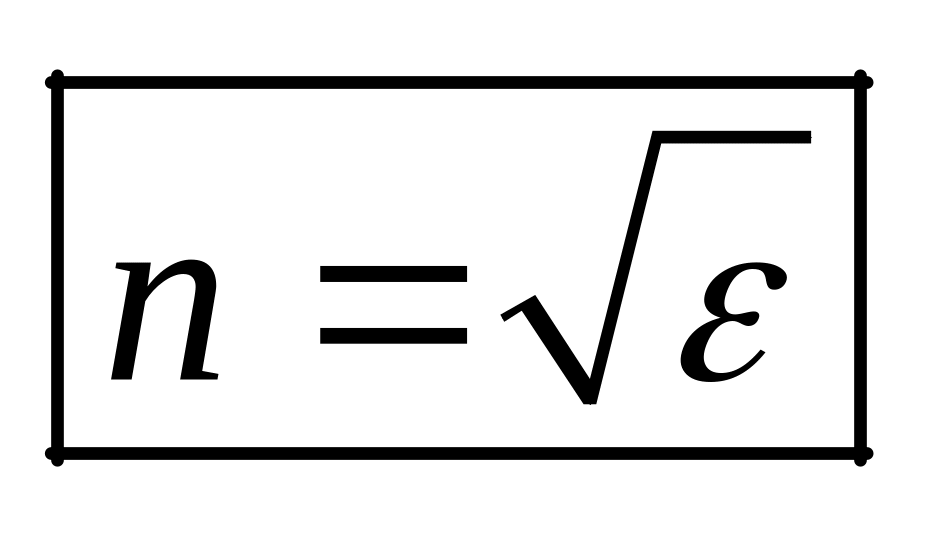, где с = 310⁸ м/с – скорость света в вакууме,  - диэлектрическая проницаемость среды. Среда с большим показателем преломления называется оптически более плотной.

n = 1 для вакуума (воздуха), n  1 для других прозрачных сред.

• Поведение лучей подчиняется основным законам геометрической оптики.

1) в оптически однородной среде свет распространяется прямолинейно.

К огда свет достигает границы раздела двух сред с различными оптическими свойствами, он частично проходит во вторую среду, изменяя направление в случае наклонного падения, и частично возвращается в первую среду.

2) закон отражения света: Луч падающий, отраженный и нормаль, восстановленная в точке падения, лежат в одной плоскости. Угол падения равен углу отражения. .

3) закон преломления света: Луч падающий, преломленный и нормаль, восстановленная в точке падения, лежат в одной плоскости. , n₂₁ – относительный показатель преломления второй среды по отношению к первой. – закон Снеллиуса.

При падении света из вакуума (воздуха) в среду с показателем преломления n закон преломления света имеет вид: .

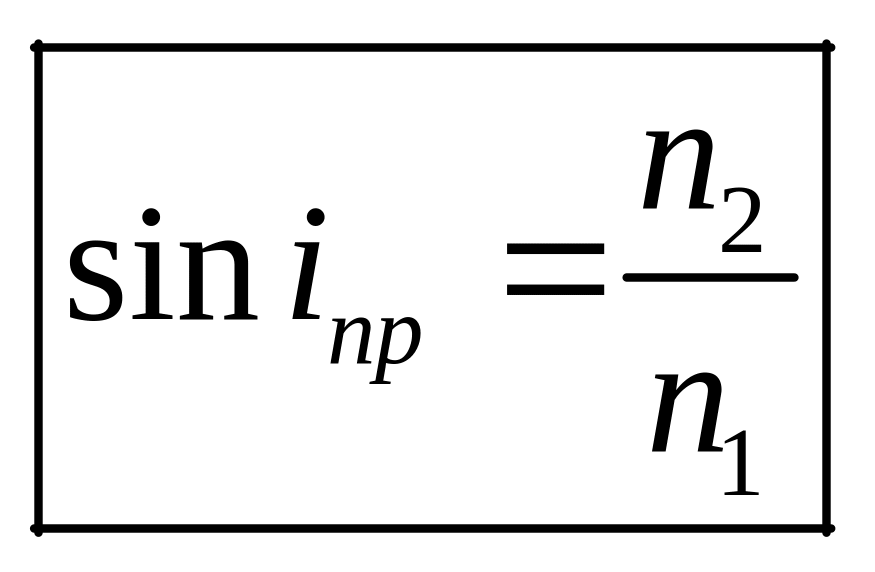• Ч астным случаем преломления света является явление полного внутреннего отражения, которое может наблюдаться только в случае падения света из оптически более плотной в оптически менее плотную среду (n₂ < n₁). Предельный угол полного внутреннего отражения i_пр . При падении света из среды с показателем преломления n в вакуум (воздух) можно пользоваться формулой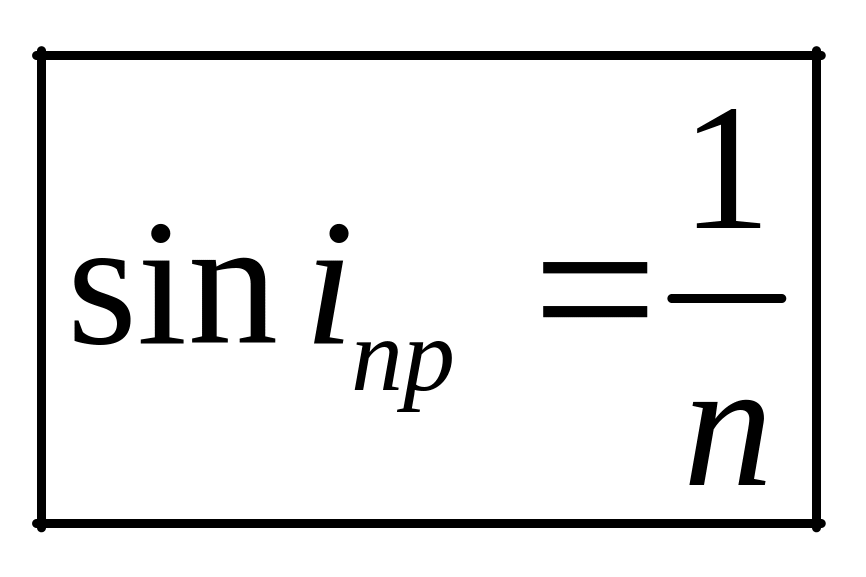 .