Задача №4.

Структура среднего размера ежемесячных дотаций и льгот, полученных домашними хозяйствами (семьями) в 2000 году (на получателя в месяц, рублей).

Таблица 6.

N п/п	Дотации и льготы на:	Федеральные округа
		Центральный		Дальневосточный
		в руб.	в % к итого	в руб.	в % к итого
1	питание	89	5	185	8,2
2	оплату транспортных расходов	78	4,3	128	5,7
3	оплату жилья и комм, услуг	61	3,4	130	5,8
4	оплату отдыха	893	49,7	889	39,6
5	оплату мед. услуг	206	11,5	560	25,0
6	содержание и обучение детей	415	23,1	227	10,1
7	прочие цели	54	3,0	125	5,6
Итого		1796	100	2244	100

Задание: Проанализируйте особенности структур, используя оценочные показатели различий структуры.

Решение:

Дополним исходные данные столбцами, где все величины выражены в % от итого.

1. Индекс структурных различий:

r=1/2*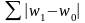 =1/2*(|5-8,2|+|4,3-5,7|+|3,4-5,6|+|49,7-39,б|+|11,5-25,0|+|23,l-10,l|+|3,0-5,6|) = = 23,1%

2. Среднее линейное отклонение:

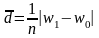=1/7*(|5-8,2|+|4,3-5,7|+|3,4-5,8|+|49,7-39,6|+|11,5-25,0|+|23,l-10,l|+|3,0-5,6|)=3,3%

3. Среднее квадратичное отклонение:

σ=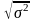 , где σ²=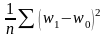

σ²=1/7*[(5-8,2)²+(4,3-5,7)²+(3,4-5,7)²+(49,7-39,6)²+(11,5-25,0)²+(23,1-10,1)²+(3,0-5,6)²]=68,28 σ= = 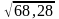= 8,26%

Например, среднее линейное отклонение показывает, что округа отличаются по любому из семи показателей в среднем на 3,3%. По одним показателям различие больше этой величины, по другим - меньше.

Задача №5.

Имеются фактические данные государственной статистики о системе интернатных учреждений для детей.

Таблица 7.

	Число учреждений (q)		В них детей, тыс. чел. (z)		Среднее кол-во детей в одном учреждении (p)
	1992 (qo)	2002 (q1)	1992 (zo)	2002 (Zl)	1992 (ро)	2002 (р1)
Дома ребенка	265	254	18,5	19,3	0,070	0,076
Детские дома	564	1244	42,4	72,3	0,075	0,058
Детские дома-интернаты	160	156	36,0	29,3	0,225	0,188
Итого			96,9	120,9

Задание:

1. Определите недостающий признак-фактор и рассчитайте его отчётные и базисные значения.

2. Рассчитайте общие индексы:

а) числа учреждений;

б) численности детей в них;

в) индекс недостающего признака-фактора.

Представьте результаты в системе взаимосвязанных индексов.

Решение:

1. Верна формула z = pq, где

z - общее количество детей, q - число учреждений,

р - среднее количество детей в одном учреждении - недостающий признак-фактор.

2. Рассчитаем общие индексы:

а). Индекс числа учреждений:

Рассчитаем индекс числа учреждений I_q по формуле I_q= = =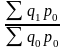

I_q= (3,3*572,3+0,5*309,3+32,9*75,5+4,5*96,4+8,0*86,2)/4805,9=1,176

б) Индекс численности детей: I_z= 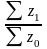= 120,9/96,9=1,25

в) Индекс среднего количества детей в одном учреждении:

I_р=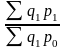 = =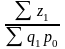120,9/146,18=0,83

Представим результаты в системе, т. е. проверим равенство I_z = I_p*I_q

I_p*I_q=0,83*l,176 = 0,97 I_z=0,97

Вывод:

В 2002 году по сравнению с 1992 годом общее количество детей увеличилось в 1,25 раза, это явилось причиной роста в 1,176 раза числа учреждений и уменьшения с коэффициентом 0,83 (на 17%) среднего числа детей в одном учреждении.