Задача №2.
Приводятся сведения по регионам Европейской части России.
Таблица 3.
Регионы
|
Числен-ность населения, млн. чел. (Ч)
|
Численность занятых в экономике в процентах от численности населения (d) |
Среднемесяч-ная зарплата одного занятого в экономике, тыс. руб. (W) |
Стоимость валового регионального продукта в среднем на |
|
одного занятого в экономике, тыс. руб. (Т) |
1 рубль стоимости в экономике, коп. (ФО) |
||||
Северный |
5,7 |
41,7 |
2,06 |
46,6 |
15,8 |
Северо-Западный |
7,9 |
45,9 |
1,69 |
35,2 |
17,1 |
Центральный |
29,2 |
45,5 |
1,85 |
46,4 |
20,9 |
Задание:
Выполните расчёт средних значений каждого показателя и укажите вид использованных средних.
Решение:
1. Средняя
численность населения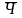
=
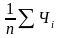=1/3*(5,7+7,9+29,2)
= 14,3 млн. чел.
Вид - простая средняя, форма - арифметическая.
2. Средняя
доля занятых в экономике:
=
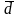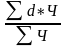
=(0,417*5,7+0,459*7,9+0,455*29,2)/(5,7+7,9+29,2)=19,3/42,8*100%=45,1%
Вид - взвешенная средняя, форма - арифметическая.
3. Среднемесячная зарплата:
=
=
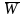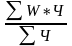(2,06*5,7+1,69*7,9+1,85*29,2)/(5,7+7,9+29,2)=79,11/42,8*100%=1,85%
Вид - взвешенная средняя, форма - арифметическая.
4. Средняя стоимость валового регионального продукта на одного занятого
=
=
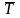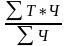(46,6*5,7+35,2*7,9+46,4*29,2)/(5,7+7,9+29,2)=1898,6/42,8=44,4
тыс.руб.
Вид - взвешенная средняя, форма - арифметическая.
5. Найти среднюю фондоотдачу нельзя, т. к. нет данных об основных фондах по каждому региону, которые используются в качестве весов при расчете фондоотдачи.
Задача №3.
Приводятся данные за 2002 год о распределении территорий РФ по стоимости валового регионального продукта в среднем на 1 руб. стоимости основных фондов в экономике.
Таблица 4.
Группы территорий РФ по уровню среднемесячного душевого дохода, тыс. руб. |
Число территорий в каждой группе |
от 7,6 до 11,3 (9,45) |
17 |
от 11,3 до 15,0 (13,15) |
33 |
от 15,0 до 18,7 (16,85) |
14 |
от 18,7 до 22,4 (20,55) |
10 |
от 22,4 и более (24,25) |
3 |
Итого: |
77 |
Задание:
1. Выполните расчёт абсолютных и относительных показателей вариации, коэффициент асимметрии и показатель моды.
2. Постройте на одном графике гистограмму и полигон распределения частот.
3. Выполните анализ полученных результатов.
Решение:
1. Найдем середины интервалов: 9,45, 13,15, 16,85, 20,55, 24,25.
Найдем средние значения интервального ряда:
=
=
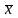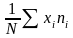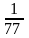(9,45*17+13,15*33+16,85*14+20,55*3)
= 14,4
Найдем дисперсию:
Dx
=
-
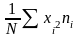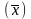2=
(9,452*17+16,852*14+20,552*10+24,252*3)-14,42
= 15,84
Найдем среднее квадратичное отклонение:
σ=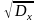
=
=
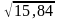3,98 абсолютный показатель вариации
Найдем коэффициент вариации V=σ/ *100%=3,98/14,4*100%=27,6% - оптимальный показатель;
Найдем
коэффициент ассиметрии Пирсона Asп
=
=
=
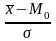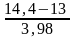0,35
Найдем
показатель моды М0
=
х0+
М0+∆*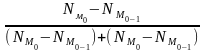
М0
=11,3+3,7*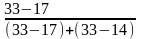
=13
∆=15,0-11,3=3,7- длина модельного интервала - интервала с наибольшей частотой;
х0 = 11,3 - левый конец модального интервала.
2. Построим на одном графике гистограмму и полигон распределения частот (рис.1.). Для большей наглядности будем брать высоту столбцов гистограммы равной соответствующей частоте, а не плотности. Острия полигона находятся над серединами соответствующих интервалов.
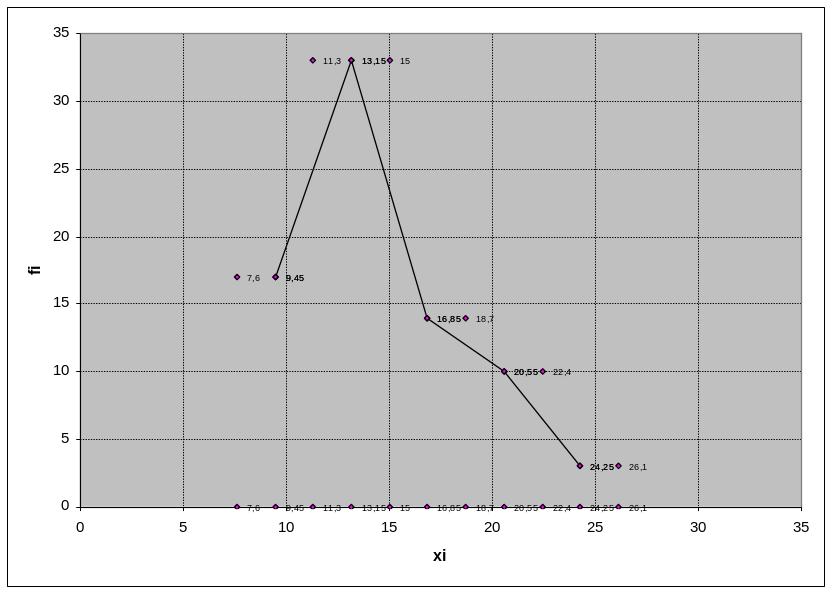
Рис.1. Гистограмма и полигон распределения частот
Сделаем выводы:
1) мода М0 и средняя принадлежат одному интервалу, следовательно, средняя типична для этой совокупности.
2) коэффициент вариации V = 27$% > 20%, следовательно, данная совокупность не является однородной.
3) коэффициент ассиметрии Пирсона Asп>0, следовательно, данная совокупность имеет правостороннюю асимметрию.