Принципиальная схема межотраслевого баланса в стоимостном выражении

Производящие отрасли	Потребляющие отрасли				Конечный продукт	Валовой продукт
	1	2		п
1
2
Условно чистая продукция
Валовой продукт

Рассматривая схему МОБ по строкам для каждой производя­щей отрасли, замечаем, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее про­дукцию отраслей и конечной продукции данной отрасли:

Формула (5.2) описывает систему из уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования.

Балансовый характер таблицы выражается в том, что

Коэффициенты прямых материальных затрат. Основу экономико-математической модели МОБ составляет технологическая матрица коэффициентов прямых затрат .

Коэффициент прямых материальных затрат показывает, сколько необходимо единиц продукции отрасли для производ­ства единицы продукции отрасли , если учитывать только прямые затраты:

Сделаем два важных предположения, необходимых для даль­нейшего рассмотрения модели Леонтьева.

• Сложившуюся технологию производства считаем неизмен­ной. Таким образом, матрица постоянна.

• Постулируем свойство линейности существующих техно­логий: для выпуска отраслью любого объема продукции необходимо затратить продукцию отрасли в количестве , т.е. материальные издержки пропорциональны объему производи­мой продукции:

Подставляя (5.4) в балансовое соотношение (5.2), получаем

Или в матричной форме

С помощью этой модели можно выполнять три вида плановых расчетов:

• задавая для каждой отрасли величины валовой продукции ,

можно определить объемы конечной продукции каждой от­расли :

• задавая величины конечной продукции всех отраслей, можно определить величины валовой продукции каждой отрас­ли :

• задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, мож­но найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. В формулах (5.7) и (5.8) символ 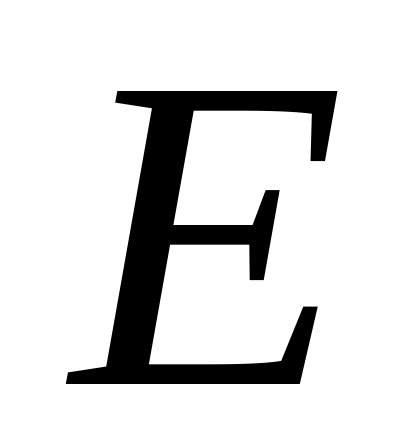обозначает единичную матри­цу порядка , а – матрицу, обратную к матрице 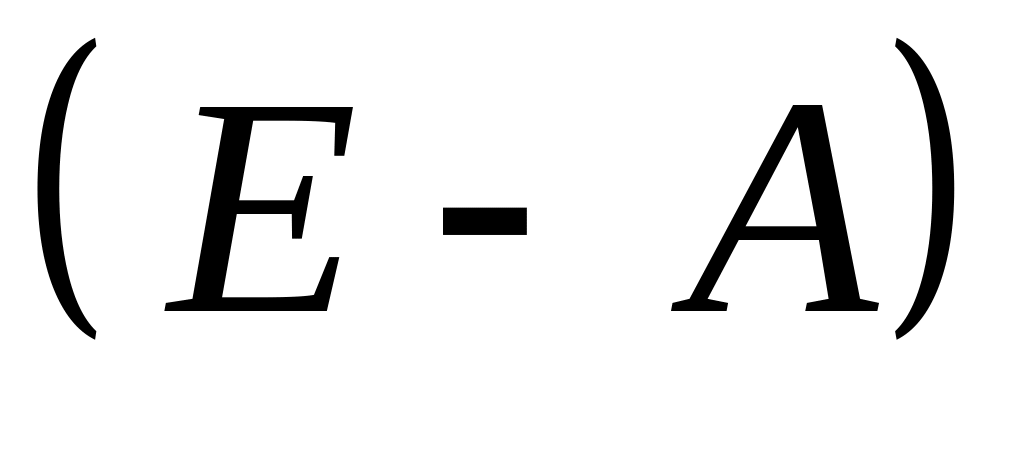. Если определитель матрицы не равен нулю, т.е. эта матрица невырожденная, то существует обратная к ней матрица.

Обозна­чим обратную матрицу через , тогда систему урав­нений в матричной форме (5.8) можно записать в виде .

Элементы матрицы называются коэффициентами полных ма­териальных затрат. Они показывают, сколько всего нужно произвести продукции отрасли для выпуска в сферу конечного использования единицы продукции отрасли .

Плановые расчеты по модели Леонтьева можно выполнять, если соблюдается усло­вие продуктивности.

Неотрицательную матрицу будем называть продуктивной, если существует такой неотрицательный вектор , что

Очевидно, что условие (5.9) означает существование положи­тельного вектора конечной продукции для модели межот­раслевого баланса (5.6).

Для решения задач приведем следующую теорему.

Теорема. Для того чтобы матрица коэффициентов прямых материаль­ных затрат была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:

• матрица неотрицательно обратима, т.е. существует обратная матрица ;

• матричный ряд сходится, причем его сумма равна обратной матрице :

• наибольшее по модулю собственное значение матрицы , т.е. решение характеристического уравнения , строго меньше единицы;

• все главные миноры матрицы , т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до , положительны.

Более простым способом проверки продуктивности матри­цы является ограничение на величину ее нормы, в данном случае на величину наибольшей из сумм элементов матрицы в каждом столбце. Если норма матрицы строго меньше единицы, то эта матрица продуктивна.

Данное условие является достаточ­ным, но не необходимым условием продуктивности, поэтому матри­ца может оказаться продуктивной и в случае, когда ее норма больше единицы.