4.5. Учет геометрических особенностей заряда

Современные твердотопливные заряды имеют сложную геометричес­кую форму канала. Наиболее часто в крупногабаритных РДТТ применя­ются заряды какально-щелевой формы, типа "звезда", "вагонное колесо" или их модификации. Поэтому важно знать, влияет ли форма заряда на его динамическое состояние.

Для этих целей используются вычислительные программы на основе численных методов расчета. В частности, в последнее время получил .широкое распространение метод конечных элементов (МКЭ), в соответс­твии с которым исследуемая область, отличающаяся от цилиндрической, разбивается на N конечных элементов простой формы (например треу­гольных, рис.4.13), а затем по определенньш законам эти элементы связываются в непрерывную область /16,21/. Математическая модель МКЭ базируется на одном из вариационных принципов, а уравнение движения заряда записывается в матричной форме:

(4.6)

где матрицы жесткости [ К ] и масс [ м 1 вычисляются суммированием по всем элементам конструкции; { 5 > - вектор неизвестных узловых перемещений; {R} - вектор нагрузки, приложенной в узловых точках по контуру тела. Двумя точками обозначено двойное дифференцирование вектора перемещений (ускорение).

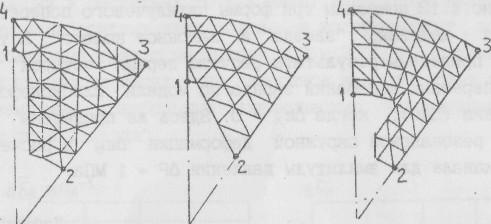
Щелевое "Звезда" "Вагонное колесо"

Рис.4.13. Схемы разбиения на конечные элементы поперечных сечений заряда

Для вынужденной задачи, когда нагрузка изменяется по закону i R > = { Ra }-exp(iu>t), уравнение движения (4.6) принимает вид, аналогичный записи закона Гука:

([ К 1 - и>²-[ М ])•{ 5_а > = (4.7)

где выражение в круглой скобке описывает динамическую жесткость системы. Индексом "а" обозначены амплитудные значения параметров.

Если в уравнении (4.6) принять { Ra > = 0, ш² = X, то задача сводится к проблеме поиска собственных значений X:

(С К 1 - Х'Г М ])•{ б_а > = 0 . (4.8)

Количество собственных значений Xi, а следовательно, и собственных частот колебаний "тределяется размерностью матриц [ К ] и [ М J, которые, в свог. очередь, определяются количеством конеч­ных элементов N.

Практическая реализация расчетов МКЭ зависит от конкретного программного обеспечения и без него невозможна /22/. Поэтому для более подробного изучения метода советуем обратиться к соответству­ющим учебным пособиям и монографиям (например /16,21/ и др.). Здесь же рассмотрим лишь некоторые результаты исследований, позво­ляющих оценить влияние геометрических особенностей заряда на его динамическое состояние.

На рис.4.13 показаны три формы пятилучевого поперечного сече­ния заряда - щелевая, "звезда" и "вагонное колесо". В табл.4.1 для этих форм приведены результаты расчета первых четырех собственных частот поперечных колебаний заряда по модели плоскодеформированно­го состояния (ДНО), когда де_х = 0. Здесь же приведены амплитудные значения резонансной окружной деформации ueq в расчетных точках 1 и 2 на канале для амплитуды давления ДР = 1 МПа.

Таблица 4.1 Динамические параметры зарядов сложной формы

Форма заряда	Собственная	Резонансная деформация
	частота, Гц	точка 1	точка 2
	135,7	0,015	0,007
Щелевая	166,9	0,072	0,019
	244,8	0,020	0,032
	266,7	0,030	0,042
	136,2	0,002
"Звезда"	201 , 3	0,122
	261 , 6	0,087
	265,5	0,085
	137,5	0,010	0,002
"Вагонное	206,0	0,009	0,004
колесо"	258,6	0,047	0.004
	263,5	0,049	0,004

Анализируя полученные результаты, убеждаемся, что сечение сложной формы обладает дополнительной степенью свободы по окружной координате 8. Поэтому колебания из одномерных (только вдоль коорди­наты г) переходят в плоские (в координатной плоскости г - 81, в связи с чем появляются дополнительные собственные частоты в доволь­но узком диапазоне 130-270 Гц, что является особенностью колебаний сложных сечений. При выгорании топлива происходит сглаживание кон­тура, который постепенно становится близким к окружности.

Результаты показывают, что с точки зрения динамики "вагонное колесо" является наименее нагруженным, т.к. при этой форме динами­ческие деформации в расчетных точках имеют наименьшую величину. По­этому для крупногабаритных двигателей, в которых могут возникнуть продольные колебания газа с частотами 100 - 300 Гц, с точки зрения динамической прочности заряд типа "вагонное колесо" может оказаться наиболее приемлемым. Наибольшую динамическую нагруженностъ могут иметь з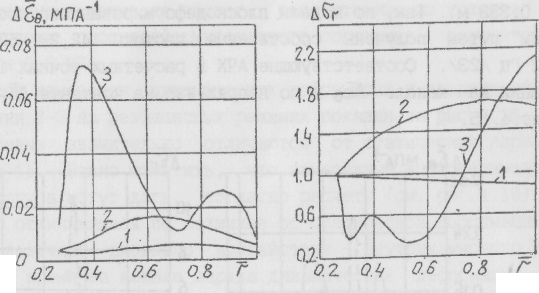 аряды типа "звезда".

Рис.4.14. Поля динамических деформаций и напряжений по линии 2-3 в заряде типа "вагонное колесо":

1 - статика; 2 - v = 160 Гц; 3 - 320 Гц

На рис.4.14 показаны поля динамических деформаций и напряжений по линии 2-3 в заряде типа "вагонное колесо". Кривые приведены для частот 160 и 320 Гц, соответствующих первым двум продольным модам колебаний газа в канале длиной L = 3,125 м. Видно, что зависимости распределения динамических деформаций и напряжений по своду заряда колебаний гага в канале длиной L = 3,125 м. ьидно, что зависимости распределения динамических деформаций и напряжений по своду заряда имеют сложный характер. По деформации корпуса трудно предположить, что на частоте 320 Гц в теле заряда (г = 0,38) динамическая дефор­мация в 45 раз превышает статическую (К_у = 45), рассчитанную при той же амплитуде давления. Чтобы перевести относительную деформацию ueq МПа"¹ в безразмерную величину, как это обычно принято, необхо­димо знать, какую долю от среднего давления Р₀ составляет амплитуда колебаний ДР. Если, например, ДР/Р₀ = 0,01, то в указанном сечении динамическая деформация составит 45% от статической. На контактной поверхности наибольший коэффициент динамического усиления по напря­жению равен 2,26. Это в несколько раз меньше, чем в случае гладкого цилиндра. Таким образом, в зарядах сложной формы наблюдается "конс­трукционное демпфирование" - дополнительное снижение уровня динами­ческих напряжений, обусловленное формой заряда.

Сравнительные результаты расчетов по одномерной и плоской мо­делям можно рассмотреть на примере 4- щелевого заряда (R= 1 м, гк = 0,333 м). Так, по модели плоскодеформированного состояния рас­четным путем получены собственные частоты 42,2; 63,7; 87,2; 131,2 Гц /23/. Соответствующе АЧХ в расчетных точках 1-4 ( по де­формации на канале Д1е и по напряжению на контакте Дб_г) приведены на рис.4.15.

jn			I
с			\
1			!
ч		V,	Ч	рч
	_^*s-	№	&
			H		--=_{e
i	K	1 8C	> f2i	? /<?	9 V.fu

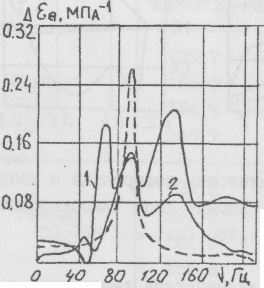
Рис.4.15. АЧХ в расчетных точках щелевого заряда: 1- точка 1; 2- точка 2; 3- точка 3; 4- точка 4; -----— щелевой канал; - - - - гладкий канал

Приведенные на рис.4.14 результаты подтверждают наличие в рассматриваемом диапазоне частот размытой резонансной области, что приводит к необходимости учитывать вязкоупругие потери во всем рассматриваемом частотном диапазоне. Это значительно усложняет анализ при практическом использовании результатов на этапе проекти­рования двигателя.

В то же время рассчитанные по одномерной модели (для гладкого цилиндрического канала) АЧХ вписываются в резонансную область час­тот и имеют единственную резонансную частоту радиальных колебаний 87,2 Гц (рис.4.15, штриховая кривая). При этой частоте рассчитанные для гладкого цилиндра резонансные деформации и напряжения имеют на­ибольшую величину, что при учете их значений в расчете идет в запас прочности заряда. Так, например, если ДР = 0,1 МПа, то по одномер­ной модели резонансные значения окружной деформации на канале и ра­диального напряжения на контакте будут соответственно 0,025 и 1,1 МПа. В то же время наибольшие значения деформации и напряжения в рассматриваемом диапазоне частот, рассчитанные из условия резо­нанса по модели плоскодеформированного состояния, соответственно равны 0,02 и 0,3 МПа.

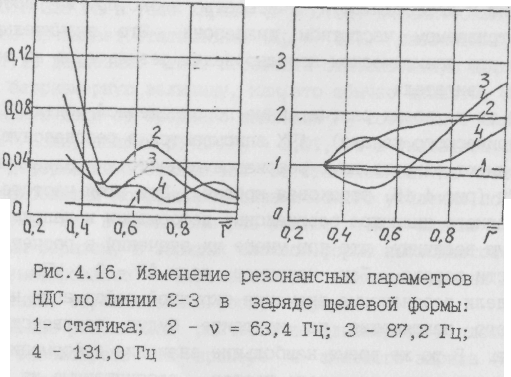
Характер изменения динамических деформаций и напряжений в за­ряде по линии 2-3 на резонансных режимах показан на рис.4.16. Дина­мические кривые значительно отличаются от статических параметров НДС (кривые 1).

Важно отметить, что замеренные в эксперименте де­формации корпуса могут дать, согласно расчету (см. рис.4.16), зна­чения, мало отличающиеся по величине от статической деформации при одинаковой величине входного воздействия - внутрикамерного давле­ния. В то же время на канале заряда динамические деформации могут быть существенно выше деформаций, рассчитанных при том же давлении по статической модели. Эту особенность следует учитывать при оценке работоспособности заряда, например, в условиях продольной акусти­ческой неустойчивости крупногабаритных РДТТ. Как и для гладкого ци­линдрического канала, в районе резонансных частот динамические нап­ряжения в этом случае возрастают к корпусу и имеют наибольшую вели­чину при частоте 87,2 Гц.

Другой моделью, используемой для оценки динамического повеле­ния заряда, является модель осисимметричного состояния (ОСС) /22/. когда параметры НДС в окружном направлении 8 не меняются, а зависят только от координат г и х. Для примера на рис.4.17 приведены АЧХ

uSa.MfT/T

&б>

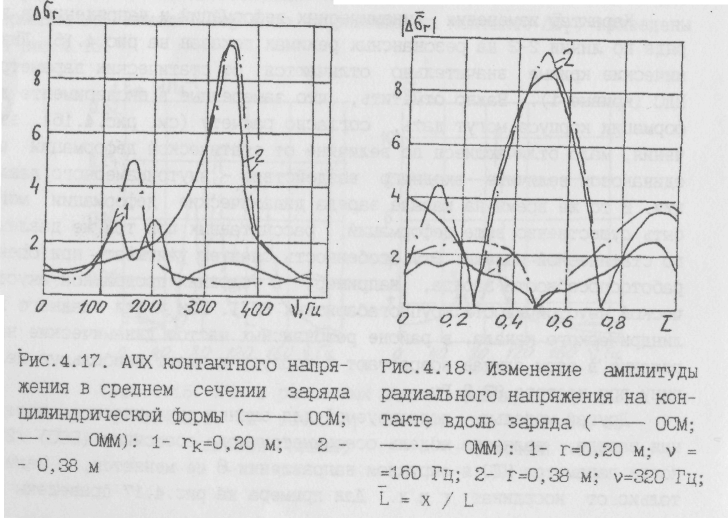
контактного напряжения в среднем сечении заряда с цилиндрическим каналом длиной L = 3,125 м и наружным радиусом R = 0,5 м для двух значений радиуса канала: гк= 0,2 м - начальное значение; гк= 0,38 м - момент выгорания, когда основная частота радиальных колебаний заряда совпадает с частотой 2-й моды продольных колебаний газа (320 Гц). Расчеты по модели ОСС для начальной геометрии дают резо­нансную область частот, в которой два пика - при 135 и 200 Гц. По одномерной модели в данной частотной области наблюдается только один радиальный резонанс при частоте 161,6 Гц. При выгорании заряда для рассмотренного среднего сечения различие в АЧХ уменьшается и, например, при гк = 0,38 м (см. рис.4.17) практически исчезает. Ре­зонансная частота по осесимметричной модели равна 319,5 Гц, по од­номерной модели - 322,9 Гц.

На рис.4.18 представлено изменение амплитуды колебаний относи­тельного радиального напряжения на контакте при частотах 160 Гц (1-я газовая мода, радиус канала в среднем сечении 0,2 м) и 320 Гц (2-я газовая мода, гк = 0,38 м).

В заключение отметим, что в динамике сложных форм вместо коэф­фициента концентрации напряжений, который применяется в статике /4/, более обоснованно использовать понятие коэффициента усиления как отношения динамической компоненты НДС к соответствующей статичес­кой, рассчитанной для той же формы заряда при давлении, равном амп­литуде колебаний давления в камере.

НЕУСТОЙЧИВОСТЬ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ.

ПРИМЕРЫ РАСЧЕТОВ КОЛЕБАНИЙ.

ИССЛЕДОВАНИЕ СОБСТВЕННЫХ ЧАСТОТ КС.

Экспериментальная установка на «холодном» газе.

1.Критерии подобия

Опираясь на теорию размерностей и подобия, рассмотрим общую схему построения алгоритма моделирования и создание для этой цели экспериментальной установки. Основные задачи моделирования и создания установки на этом этапе включают:

- Анализ факторов и условий работы РДТТ;

- Выбор общего математического аппарата, описывающего процессы течения газа в камере сгорания, как натурного, так и модельного двигателя;

- Формирование на основании математической модели определяющих параметров и построение базы критериев подобия;

- Определение условий моделирования и построение на основе выбранных объектов подобия математического аппарата, позволяющего вести пересчёт полученных результатов на натурный объект;

- Выбор рабочего тела и условий его подвода к модельному двигателю;

- Моделирование газоприхода с «горящей» поверхности модельного двигателя.

Теория подобия является необходимым инструментом всякого экспериментального исследования. Так как для рассматриваемого процесса движение газа в камере сгорания двигателя полное моделирование невозможно, особое значение имеет выбор состава определяющих критериев и оценка их значимости. Такой состав должен обеспечить достаточно полное моделирование основных свойств потока с помощью относительно простых технических решений.

Смысл моделирования заключается в том, чтобы дать необходимые ответы о характере эффектов и влиянии различных величин, связанных с явлениями в натурных условиях при формировании течения газа в камере сгорания РДТТ. Из теории подобия следует, что два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчётом, который аналогичен переходу от одной системы единиц измерения к другой, то есть подобными физическими процессами будут такие явления одной природы, которые протекают в геометрически подобных пространственных системах, и, у которых значения переменных, характеризующих одноимённые явления, пропорциональны в сходственных точках и гомохронные моменты времени. Такое преобразование переменных, при котором значение каждой из них меняется в определённое число раз, называется подобным преобразованием. Необходимым и достаточным условием подобия двух явлений является постоянство численных безразмерных комбинаций, образующих базу.

Предположим, что изучаемое явление зависит от n переменных ( ). С помощью подобного преобразования, то есть преобразования вида каждого из перечисленных переменных, изучаемое явление можно свести к подобному ему явлению. Так, если в любой точке системы значения переменных соответствуют , то в сходной точке подобной ей системы в гомохронный момент времени значения переменных будут соответствовать , причём , ,…, , где множители подобного преобразования (константы подобия).

Однако не любая совокупность значений множителей сводит изучаемое явление к подобному.

Действительно, так как переменные характеризуют изучаемое явление, то между ними существует связь, которая математически выражается уравнениями (в данном случае уравнениями движения вязкого газа в канале камеры сгорания РДТТ).

Пусть изучаемое физическое явление описывается в общем виде системой уравнений:

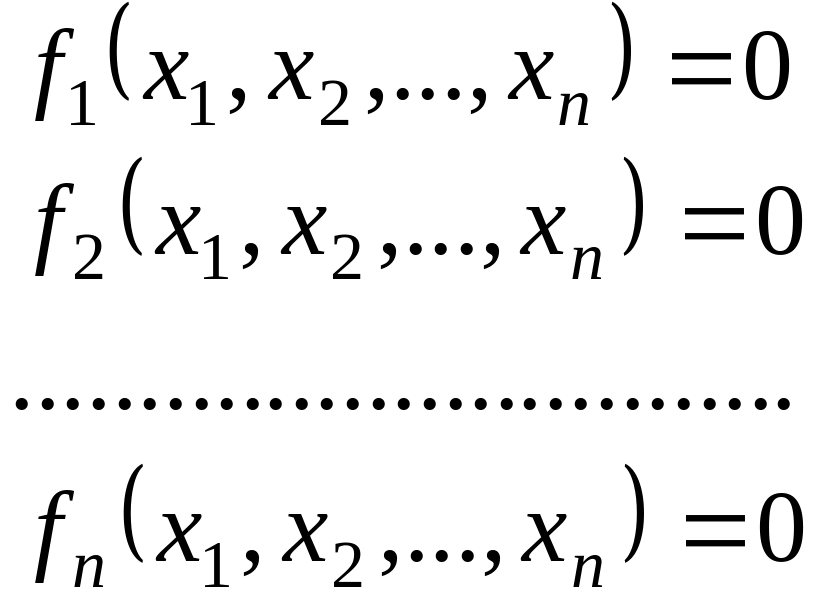(1.1)

Путём преобразования переменных система уравнений (1) для подобного явления будет иметь вид:

(1.2)

Если системы уравнений (1) и (2) описывают подобные явления, то они должны иметь совместное решение. Свойство уравнений оставаться неизменными при каких-либо преобразованиях, входящих в них величин, называется инвариантностью рассматриваемых уравнений относительно произведённых преобразований. Из математики известно, что две системы инвариантны, если множители преобразования выйдут за знак функции (f) системы (2), то есть система преобразуется к виду:

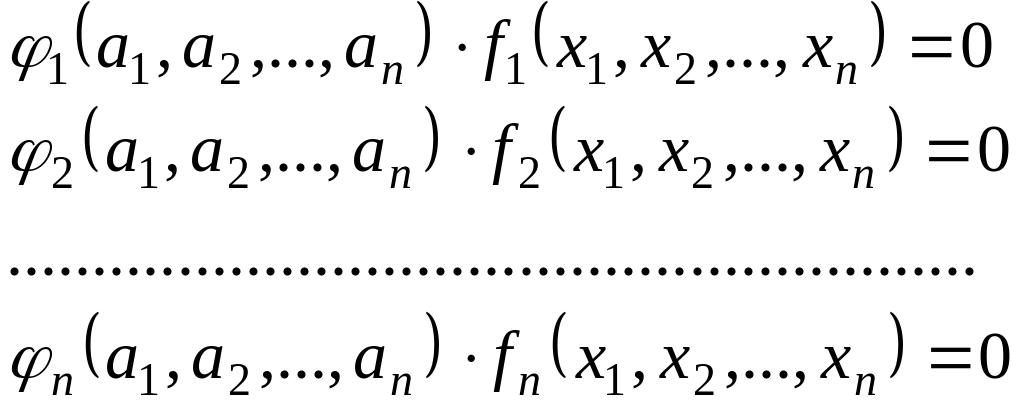(1.3)

Системы уравнений (1) и (2) имеют совместное решение в том случае, если имеет место следующее соотношение:

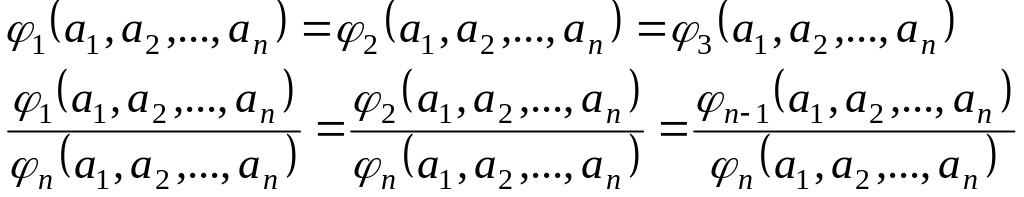(1.4)

Соотношение (3) обуславливает инвариантность уравнений системы (2) относительно подобного преобразования входящих в них переменных ( ) и носит название обуславливающих уравнений. Следовательно, между множителями подобного преобразования существует связь, которая может быть описана следующими теоремами подобия, (?).

Первая теорема подобия гласит: «У подобных явлений, описываемых уравнениями, их инварианты относительно подобных преобразований, входящих в эти уравнения переменных параметров одинаковы.» На выбор совокупности множителей подобного преобразования не влияет количество рассматриваемых параметров, описывающих процесс.

Исходная система уравнений пригодна для описания бесконечного множества явлений одной и той же природы. Конкретное явление может быть выделено из класса явлений, задаваемых условием однозначности. Задание условия однозначности включает:

- геометрические особенности: форма ограничивающих поверхностей или пространства, их размер, в котором осуществляется тот или иной процесс;

- особенности протекания процесса во времени;

- начальные условия, определяющие распределение по пространству основных величин: давления, плотности газа, скорости, температуры и пр.;

- граничные особенности, включающие распределение по границам определяющих параметров (массоприход, давление вдува и пр.).

- физические и химические особенности среды, в которой осуществляется процесс.

Математический аппарат вопросов о единстве решений составленных уравнений и присоединенных к ним условий однозначности часто бывает чрезвычайно сложным, поэтому обычно исходя при этом из соображений физического характера изучаемого процесса.

В теории подобия вводится понятие группы подобных явлений, в пределах которой можно производить обобщение экспериментальных данных. Первая теорема подобия устанавливает необходимый признак существенных явлений, относящихся к одной группе. Если обуславливающие уравнения вместо множителей подобного преобразования поставить их выражение через переменные, то необходимые условия существования группы подобных явлений можно записать следующим образом:

k₁=i dem, k₂=i dem,…, k_n=i dem.

где k_i - безмерные величины, составленные из переменных , называемые критериями подобия.

Вторая теорема подобия утверждает, что «уравнения, выражающие связь между переменными могут быть преобразованы в уравнение связи между критериями».

Критерии подобия, выделенные из исходных уравнений можно разбить на две категории. К первой категории критериев подобия, называемых определенными, относят такие критерии, которые составлены только из величин входящих в условия однозначности. Если же выражения для критерия имеет хотя бы одну из переменных, не входящих в условие однозначности, то такой критерий называют неопределяющим.

Первые две теоремы подобия исходят из существования подобия, как известного фактора, который наперед задан. Третья теорема наоборот, устанавливает признаки, по которым можно узнать подобны ли два явления друг другу. Она гласит: «Равенство определяющих критериев подобия, наряду с подобием условий однозначности и инвариантности исходных уравнений, необходимо и достаточно для подобия рассматриваемых явлений».

Таким образом, третья теорема подобия указывает каким образом практически можно осуществить подобные явления, что бы результаты экспериментов были справедливы для явлений одной группы.

Пользуясь второй и третьей теоремами подобия критериев, можно показать что каждый из неопределяющих критериев подобия есть однозначная функция совокупности всех определяющих критериев подобия.

Для составления базы определяющих критериев рассмотрим неустановившееся турбулентное движение вязкого газа в осесимметричном канале сложной формы с газоприходом с его боковых поверхностей и истечение его через критическое сечение сопла. В общем случае при изучении неустановившегося движения газа мы должны вводить в число определяющих параметров время (τ), являющихся переменной величиной. При рассмотрении механизма подобных движений мы встречаемся с изменением численного значения параметра – времени (τ) за счет изменения масштаба и за счет изменения времени процесса движения. В связи с этим мы остановимся на некоторых общих значениях, связывающих кинематически подобные неустановившиеся движения.

Пусть мы имеем неустановившиеся кинематически подобные движения, представляющие течение вязкого газа. Система уравнений, описывающих этот процесс включает полные уравнения Новье-Стокса, уравнение состояния, уравнение энергии и уравнение связи.(?)

Для определения акустических возмущений, связанных с движением и обтеканием элементов рабочего тракта РДТТ, уравнение сохранения количества движения можно рассматривать как совокупность двух уравнений - стационарного, или невозмущённого, и пульсационного. Решение пульсационного уравнения для продольных колебаний газа в стационарном потоке можно представить в виде:

(1.5)

С учётом уравнения для акустического давления (1.5) система определяющих параметров для такого потока в канале камеры сгорания РДТТ и модельного двигателя будет состоять из следующих величин:

(1.6)

Состояние движений систем в каждый момент времени определяется начальными возмущениями (возмущения газа в момент времени τ=0) и свойствами инерции газа, то есть плотностью (ρ) и вязкого газа (μ).

На основе анализа условий моделирования газодинамических процессов в камере сгорания РДТТ, размерные определяющие параметры (1.6) могут быть выражены критериями подобия:

(1.7)

На основании второй и третьей теоремы теории подобия рассматриваемые процессы течения газа в камере сгорания РДТТ будут подобны, если будут выражены условия равенства критериев (1.7):

(1.8)

При этом критерии: геометрический ( ) и гомохронный ( ) должны не зависеть от изменения координат и времени, то есть: .

Рассмотрим совокупную базу критериев подобия (1.7), моделирование процессов течения газа в камере сгорания РДТТ и условия их соблюдения.

Для механических систем принято разделение безразмерных критериев на группы, отличающиеся по функциональному назначению. Различают линейное и геометрическое, гомохронное или временное подобие. Эта группа критериев относится к обязательным условиям выполнения при моделировании и характеризуется масштабом соответствующих величин, то есть необходимым и достаточным условием соблюдения указанных критериев является постоянство отношений их одноимённых величин:

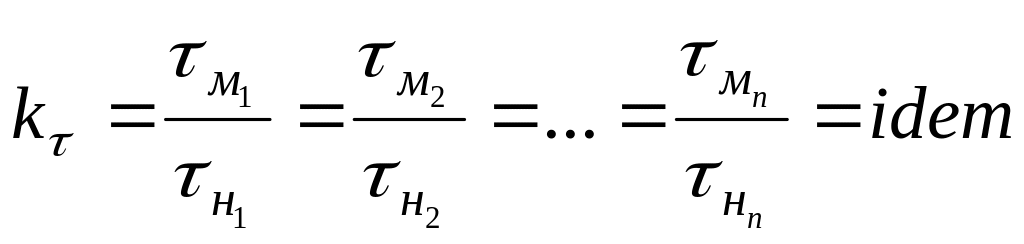(1.9)

(1.10)

В группе критериев выделяется кинематическое подобие, которое связывает в сходных точках соответствующих потоков их абсолютные скорости:

(1.11)

Применительно к моделированию газодинамических процессов в камере РДТТ к группе кинематических критериев подобия можно отнести коэффициент инвариантности по скорости чисел Маха (М) и Струхаля (Sh). Их выражения можно записать:

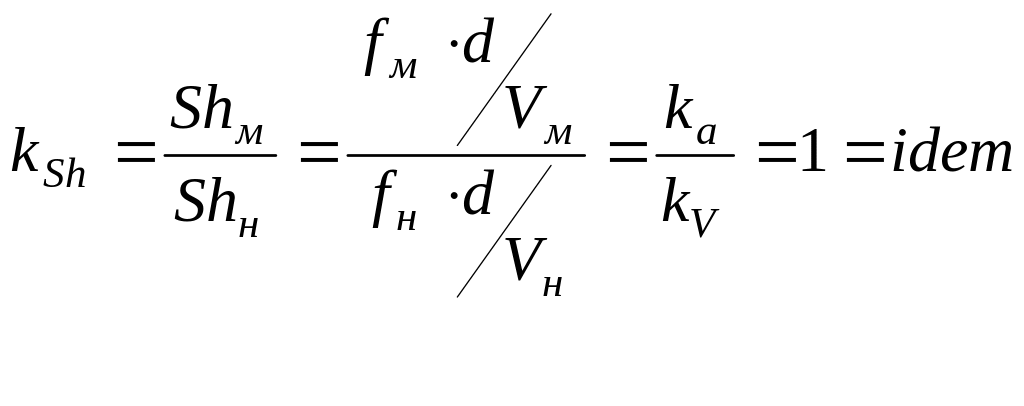
Коэффициент инвариантности ( ) необходимо отнести к термодинамическим параметрам, т.к. скорость звука в газовом потоке определяется через параметры газа:

К сложным критериям подобия относятся динамические (Re, q) и термодинамические (γ, Pr), (1.7). Под динамическим подобием понимается такое подобие, при котором соблюдается подобие многоугольников всех сил, действующих в геометрически подобных точках пространства или тела. Условие динамического подобия в общем виде запишется:

(1.12)

Термодинамическое подобие – это подобие, при котором в газовом потоке в геометрически подобных точках пространства соблюдается постоянное соотношение относительного изменения величины полной энергии:

(1.13)

Подобие называется полным, если во всем пространстве определяющем соответствующие сравниваемые процессы, выполняются постоянными соотношениями вышеперечисленные критерии, т.е.:

Если хотя бы одно из условий равенства критериев подобия системы (1.7) будет не соблюдено, т.е. при переходе из одной исследуемой зоны в камере сгорания РДТТ в другую параметры изменяются на постоянную и известную величину, то такое моделирование называют частичным:

.

К условному подобию прибегают, когда при постановке опытов не представляется возможным применить даже частичное подобие. В этом случае коэффициент инвариантности критериальных чисел будет переменной величиной, зависящей как от координаты, так и от времени:

.