4.3. Резонансное состояние заряда

Наибольшую динамическую нагруженность имеет заряд при резонан­се, когда запас по частоте Av = 0. Рассмотрим влияние основных па­раметров системы на динамические напряжения и деформации при резо­нансе.

Наибольшее влияние на величину резонансных параметров НДС за­ряда оказывает угол сдвига фаз фе, определяющий вязкоупругие свойс­тва топлива. В частности, расчетным путем установлено, что резо­нансные значения напряжений и деформаций обратно пропорциональны углу сдвига фаз фе (рис.4.6). Эта величина оказывает существенное влияние лишь в узком диапазоне частот резонансного пика (см. рис.4.4). Поэтому при практических расчетах вязкоупругие потери можно учитывать только при частотах, соответствующих условию , которое позволяет решать динамическую задачу по упругой модели в широком диапазоне отношения ry. / R, изменяющегося при выгорании топлива. И только в узком резонансном диапазоне следует учитывать реальные потери в топливе по вязкоупругой модели.

В зависимости от геометрических параметров заряда и корпуса, а также от механических свойств топлива и конструкционного материала корпуса возможно изменение резонансных напряжений и деформаций в широких пределах. Фрагмент такого анализа приведен на рис.4.7 и 4.ь. Видно, что для заданной величины Мк = 0,2 резонансные значения напряжений на канале и на контакте при феленных уровней. Так окружное напряжение на канале при любых соотно­шениях механических и геометрических параметров конструкции прини­мает значение, немногим более двадцатикратного увеличения амплитуды колебаний давления. Аналогично усиления радиального напряжения на контактной поверхности при указанных исходных данных не могут пре­вышать 14-КБатного увеличения амплитуды осциллирующего давления

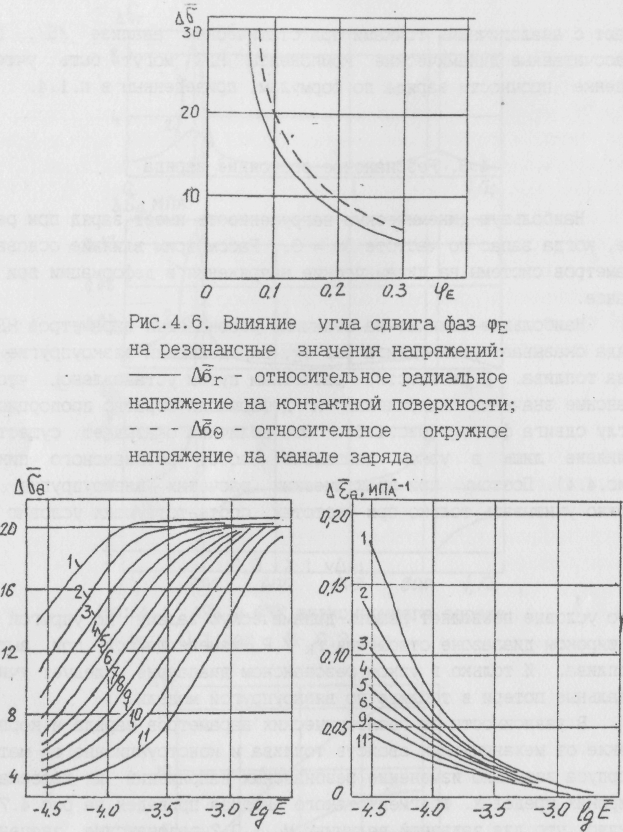
Рис.4.7. Резонансные относительные значения напряжений (а) и деформаций (б) на канале заряда. (Мх = 0,2; фе = 0,1 рад; ц_п = 0,495; Ф_и = 0): 1- Б - 10~³; 2- 2-W~³; 3- 3 10~³; 4- 4-10~³; 5- 5-Ю""³; 6- 7,5-10~³; 7- 10~²; 8- 1,5'10~²; 9- 2-10~²; 10- 3-Ю"²; 11- 5'10~²

.

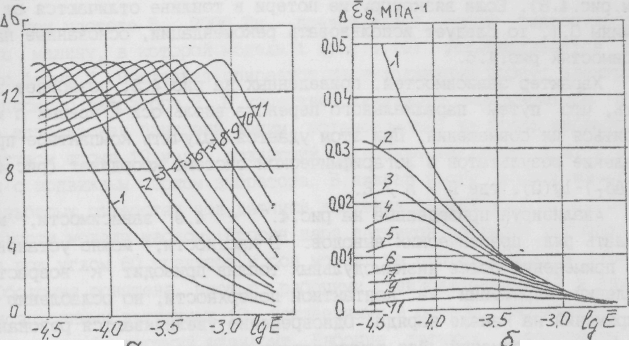
Рис.4.8. Резонансные относительные значения напряжений (а)

и деформаций (б) на контактной поверхности заряда 04-0,26: фе = 0,1 рад ; ц_п = 0,495; ^ =0): 1- К = 10~³; 2- 2'10"³; 3- 3-Ю"³; 4- 4-'КГ³; 5- 5-Ю"³; б- 7,5'10~³; 7- 10"²; 8- 1,5-1СГ²; 9- 2-Ю""²; 10- 3-Ю'²; 11- 5'10"²

-1

П

Рис.4.9. Зависимость контактного резонансного напряжения от относительной жесткости системы: 1- M_k = 0,2; 2- 0.3; 3- 0,4: 4- 0,5; 5- 0,5; б- 0,7; 7- 0,8

(см.рис.4.8). Если вязкоупругие потери в топливе отличаются от ве­личины 0,1, то следует использовать рекомендации, основанные на за­висимостях рис.4.6.

Характер зависимостей, приведенных ка рис.4.8, позволяет заме­тить, что путем параллельного переноса ~долъ оси Е кривых h можно добиться их совмещения. При этом удается получить компактное предс­тавление результатов в логарифмической системе координат (рис 4.9): 1в(Дб_г)-1гШ), где П = h /1.

Анализируя приведенные на рис.4.7 - 4.9 зависимости, можно сделать ряд практических выводов. В частности, можно установить, что применение более низкомодульных топлив приводит к возрастанию усилений напряжений на контактной поверхности, но ослаблению этих напряжений на канале заряда. Одновременно увеличиваются резонансные значения деформаций. Для таких топлив из динамических условий кор­пус должен быть более жестким. Однако для реальных конструкций диа­пазон изменения параметра П, как правило, 5 ... 50, что, согласно зависимостям рис.4.9, приходится как раз на максимальные уровни ре­зонансных значений напряжений.

При выгорании заряда резонансные компоненты НДС имеют тенден­цию к росту. Коэффициент Пуассона топлива при д_п -» 0,5 также приво­дит к росту динамических компонентов.

Таким образом, основные расчетные точки по своду заряда, в ко­торых необходимо определять динамические компоненты НДС при колеба­ниях давления в камере, совпадают с условиями статики.