Метод множителей Лагранжа.

Метод множителей Лагранжа, метод нахождения условного экстремума функции  , где  , относительно   ограничений  , где   меняется от единицы до  .

Составим функцию Лагранжа в виде линейной комбинации функции   и функций  , взятых с коэффициентами, называемыми множителями Лагранжа —  :

где  .

Составим систему из   уравнений, приравняв к нулю частные производные функции Лагранжа   по   и  .

Если полученная система имеет решение относительно параметров   и  , тогда точка   может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.

Алгоритм обобщенного метода множителей Лагранжа.

Сначала все ограничения отбрасываются, и решается задача безусловной максимизации ЦФ. Находится ее стационарная точка и проверяется ее допустимость. Если оказалось, что эта точка принадлежит ОДР, то процесс вычислений завершается, так как в силу выпуклости задачи (14) – (15) найденная точка является ее решением.

Если же найденная точка не допустима, то формируется новая задача, которая состоит в максимизации ЦФ с учетом первого ограничения задачи. Однако это ограничение записывается не как неравенство, а как равенство.

Получаем классическую задачу условной оптимизации вида:

Z = f (x₁,…, x_n) ® mах,

g₁(x₁,…, x_n) = b₁.

Для ее решения используется метод множителей Лагранжа. Выписывается функция Лагранжа

L(x₁,…, x_n, λ) = f (x₁,…, x_n) + λ (b₁ – g₁ (x₁,…, x_n))

и решается система уравнений, определяющая стационарные точки этой функции:

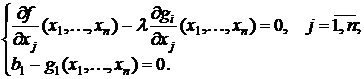
Если в результате получен вектор решения   такой, что вектор   допустим в исходной задаче и λ^* ≥ 0, то это означает, что   — искомая точка оптимума. Если же оказалось, что λ^* < 0 или вектор   недопустим в исходной задаче, то вместо первого ограничения берется второе ограничение и рассматривается задача

Z = f (x₁,…, x_n) ® mах,

g₂(x₁,…, x_n) = b₂.

Эта задача также решается методом множителей Лагранжа. Если ее решение опять не является точкой оптимума исходной задачи, то берется третье ограничение и т.д. Если последовательный перебор отдельных ограничений не приводит к желаемому результату, то рассматриваются задачи с двумя ограничениями, затем тремя ограничениями и так до тех пор, пока не будет найдено оптимальное решение исходной задачи.

Замечание. Если исходная задача содержит ограничения типа равенства, то их нужно включать во все формируемые задачи.

Условные и безусловные задачи НП.

Введение барьерных штрафных функций.

Основная задача метода штрафных функций состоит в преобразовании задачи минимизации функции

с соответствующими ограничениями, наложенными на х, в задачу поиска минимума без ограничений функции

Функция   является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию Z, т.е. увеличивала её значение.В этом случае минимум функции Z будет находиться внутри области ограничений. Функция  , удовлетворяющая этому условию, может быть не единственной. Задачу минимизации можно сформулировать следующим образом:

минимизировать функцию 

при ограничениях  .

Функцию   удобно записать следующим образом:

где r – положительная величина.

Тогда функция   принимает вид

.

Если х принимает допустимые значения, т.е. значения, для которых  , то Z принимает значения, которые больше соответствующих значений   (истинной целевой функции данной задачи), и разность можно уменьшить за счет того, что r может быть очень малой величиной. Но если х принимает значения, которые хотя и являются допустимыми, но близки к границе области ограничений, и по крайней мере одна из функций   близка к нулю, тогда значения функции  , и следовательно значения функции Z станут очень велики. Таким образом, влияние функции   состоит в создании «гребня с крутыми краями» вдоль каждой границы области ограничений. Следовательно, если поиск начнется из допустимой точки и осуществляется поиск минимума функции   без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая r достаточно малой величиной, для того чтобы влияние   было малым в точке минимума, мы можем сделать точку минимума функции  без ограничений совпадающей с точкой минимума задачи с ограничениями.

Введение штрафных функций Фиакко - Мак-Кормика.

Штрафные функции Розенброка.

Функция Розенброка — невыпуклая функция, используемая для оценки производительности алгоритмов оптимизации, предложенная Ховардом Розенброком  в 1960 году. Считается, что поиск глобального минимума для данной функции является нетривиальной задачей.

Является примером тестовой функции для локальных методов оптимизации. Имеет минимум 0 в точке (1,1)].

Значение функции Розенброка для двух переменных в окрестности точки  .

Функция Розенброка для двух переменных определяется как:

Она имеет глобальный минимум в точке   где  .

Встречаются два классических варианта многомерного обобщения функции Розенброка.

В первом случае, как сумма   несвязанных двумерных функций Розенброка:

]

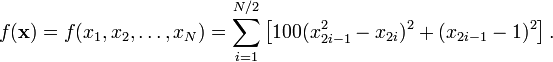Более сложным вариантом является:

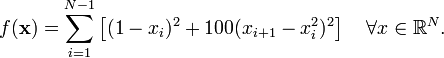
Существует также вероятностное обобщение функции Розенброка, предложенное 

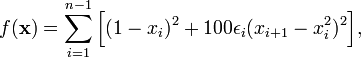
где случайные переменные   являются непрерывно распределёнными Unif(0,1).