Нелинейное программирование (НП). Классификация задач НП.

Задачами нелинейного программирования называются задачи математического программирования, в которых нелинейны и (или) целевая функция, и (или) ограничения в виде неравенств или равенств.

Задачи нелинейного программирования можно классифицировать в соответствии с видом функции F(x), функциями ограничений и размерностью вектора х (вектора решений).

Классы Квадратичное программирование Динамическое программирование Вероятностное программирование

Решение задач квадратичного программирования. Приведение квадратичных функций к каноническому виду.

Квадратичной формой n переменных x1 x2…xn ,принимающих числовые значения , называется числовая функция вида

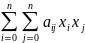
где 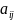- числа, называемые коэффициентами квадратичной формы.

Квадратичная форма называется канонической (имеет канонический вид), если коэфициенты 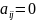при 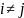, то есть, если матрица квадратичной формы диагональная и следовательно

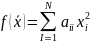
Решение задач квадратичного программирования. Квадратичные формы.

Квадратичной формой F , зависящей от n переменных x₁,x₂, … ,x_n называется функция вида

F = a11 x12 + 2a12 x1 x2 + a22 x22 + … + ann xn2 = i,j= 1n∑ aij xi xj ,

где a_ij = a_ji (i,j = 1, … ,n) — вещественные числа.

Симметричная матрица A = (a_ij) (i,j = 1, … ,n) называется матрицей квадратичной формы F .

Если переменные x₁, x₂,  … , x_n интерпретировать как координаты переменного вектора x в некотором ортонормированном базисеe₁, e₂,  … , e_n n –мерного евклидова пространства, то матрица A есть матрица некоторого самосопряженного оператора ^A в этом базисе. Тогда

i,j= 1n∑ aij xi xj = (^Ax, x).

Действительно, пусть x = i= 1n∑ x_i e_i и его образ y = ^A x . Тогда i–я координата образа y_i = (^A x)_i = j= 1n∑ a_ijx_j . Подставляя это выражение в формулу для скалярного произведения в ортонормированном базисе, получим

(^Ax, x) = i= 1n∑ xi yi = i,j= 1n∑ aij xi xj = F

Если рассматривать матрицу квадратичной формы как матрицу некоторого самосопряженного оператора, то, очевидно, ее вид будет зависеть от выбора базиса.

Базис, в котором квадратичная форма F имеет вид

F = i= 1n∑ λi (xi')2

(1)

называется каноническим базисом, а выражение (1) — каноническим видом квадратичной формы.

Основания теории оптимизации (теоремы о необходимости и достаточности существования экстремума функции многих переменных).

Необходимые условия экстремума.

Пусть функция u=f(x 1 ,x 2 ,…,x n ) определена в области D и (x 1 0 ,x 2 0 ,…,x n 0 ) будет внутренней точкой этой области.

Говорят, что функция u=f(x 1 ,x 2 ,…,x n ) в точке (x 1 0 ,x 2 0 ,…,x n 0 ) имеет максимум (минимум), если её можно окружить такой окрестностью

(x 1 0 x 1 0 x 2 0 x 2 0 x n 0 x n 0 )

что бы для всех точек этой окрестности выполнялось неравенство

f(x 1 ,x 2 ,…,x n )<f(x 1 0 ,x 2 0 ,…,x n 0 )

Если эту окрестность взять настлько малой, что бы знак равенства был исключён, т. е. чтобы в каждой её точке, кроме самой точки (x 1 0 ,x 2 0 ,…,x n 0 ) выполнялось строгое неравенство

f(x 1 ,x 2 ,…,x n )<f(x 1 0 ,x 2 0 ,…,x n 0 )

то говорят, что в точке (x 1 0 ,x 2 0 ,…,x n 0 ) имеет место собственный максимум (минимум), в противном случае максимум (минимум) называют несобственным.

Для обозначения максимума и минимума (как и в случае одной переменной) употребляется общий термин – экстремум.

Предположим, что наша функция в некоторой точке (x 1 0 ,x 2 0 ,…,x n 0 ) имеет экстремум,

Покажем, что если в этой точке существуют (конечные) частные производные

f x1 ’(x 1 0 ,x 2 0 ,…,x n 0 ) ,…, f ’ xn (x 1 0 ,x 2 0 ,…,x n 0 )

то все эти частные производные равны нулю, так что обращение в нуль частных производныхпервого порядка является необходимым условием существования экстремума.

С этой целью положим x 2 =x 2 0 ,…,x n = x n 0 сохраняя x 1 переменным ; тогда у нас получится функция от одной переменной x 1 :

u=f(x 1 , x 2 0 ,…,x n 0 )

Так как мы предположили, что в точке (x 1 0 ,x 2 0 ,…,x n 0 ) существует экстремум (для определенности - пуcть это будет максимум), то, в частности, отсюда следует, что в некоторой окрестности(x 1 0 - , x 1 0 + ) точки x 1 = x 1 0 , необходимо должно выполняться неравенство

f(x 1 , x 2 0 ,…,x n 0 )< f(x 1 0 ,x 2 0 ,…,x n 0 )

так что упомянутая выше функция одной переменной в точке x 1 = =x 1 0 будет иметь максимум, а отсюда по теореме Ферма следует, что

f x1 ’(x 1 0 ,x 2 0 ,…,x n 0 )=0

Таким образом можно показать, что в точке (x 1 0 ,x 2 0 ,…,x n 0 ) и остальные частные производные равны нулю.

Итак, “подозрительными” на экстремум являются те точки, в которых частные производные первого порядка все обращаются в нуль: их координаты можно найти, решив систему уравнений

f x1 ’(x 1 0 ,x 2 0 ,…,x n 0 )=0

f ’ xn (x 1 0 ,x 2 0 ,…,x n 0 )=0

Как и в случае функции одной переменной, подобные точки называются стационарными.

Замечения :Необходимое условие существования экстремума в случае дифференцируемой функции кратко можно записать так :

d f(x 1 ,x 2 ,…,x n )=0

так как, если f x1 ’= f x2 ’=…= f ’ xn , то каковы бы ни были dx 1 ,dx 2 ,…,dx n всегда

f(x 1 ,x 2 d,…,x n )= f x1 ’ dx 1 + f x2 ’ dx 2 +…+ f ’ xn dx n =0

И обратно : если в данной точке тождественно выполняется это условие, то ввиду произвольности dx 1 ,dx 2 ,…,dx n производные f x1 ’, f x2 ’,…, f ’ xn порознь равны нулю.

Обычно, рассматриваемая функция f(x 1 ,x 2 ,…,x n ) имеет (конечные) частные производные во всей области, и тогда точки, доставляющие функции экстреммы, следует искать лишь среди стационарных точек. Однако встречаются случаи, когда в отдельных точках некоторые частные производные имеют бесконечные значения или вовсе не существуют (в то время как остальные равны нулю). Подобные точки, собственно, тоже следует причислить к “подозрительным” по экстремуму, наряду со стационарными.

Иногда дается и не прибегая к достаточным условиям выяснить характер стационарной точки функции. Так, если из условия задачи непременно следует, что рассматриваемая функция имеет где-то максимум или минимум и при этом системе уравнений (5.1) удовлетворяет только одна точка, то ясно, что эта точка и будет искомой точкой экстремума функции.

Заметим, наконец, что точками экстремума непрерывной функции могут быть точки, в которых функция недифференцируема (им соответствуюя, например, острия поверхности – графика функции).