
Задача 6
Предстоит выбрать лучший из трех возможных инвестиционных проектов: ИП1, ИП2 и ИП3.
Под инвестиционными проектами можно все, что угодно: вложение средств в производство или торговлю тремя разными продуктами, покупку акций трех разных компаний, аренду трех участков земли, на которых с той или иной вероятностью предполагается наличие запасов нефти и т.д.
Допустим, что для своего осуществления упомянутые проекты требуют вложения средств в размерах х1 = 200, х2 = 300, х3 = 500 млн. руб. и могут дать прибыль в размере у1 = 100, у2 = 200, у3 = 300 млн. руб.
Риск потери этих средств по этим проектам характеризуется вероятностями на уровне р1 = 10%, р2 = 5%, р3 = 20%.
Какой проект лучше?
Рекомендации по решению
Ответить на поставленный вопрос чисто математическими средствами трудно, а то даже и невозможно. С помощью же дерева решений этот ответ найти очень просто. Дерево решений для условий данного примера представлено на рисунке 2.
Для заполнения кружков данного графика находим соответствующие математические ожидания выплат:
M(х1) = 100 × 0.9 – 200 × 0.1 = 70,
М(х2) = 200 × 0.95 – 300 × 0.05 = 175,
М(х3) = 300 × 0.8 – 500 × 0.2 = 140.
Наибольшее математическое ожидание, как мы видим, надо поставить во второй сверху кружок и повторить его в квадрате. Значит, оптимальным является решение вложить средства в ИП2.
Итак, с помощью дерева решений задача решается очень просто. Но совсем не просто подобрать для нее подходящую функцию и решить ее чисто математическим путем через нахождение экстремума соответствующей функции.
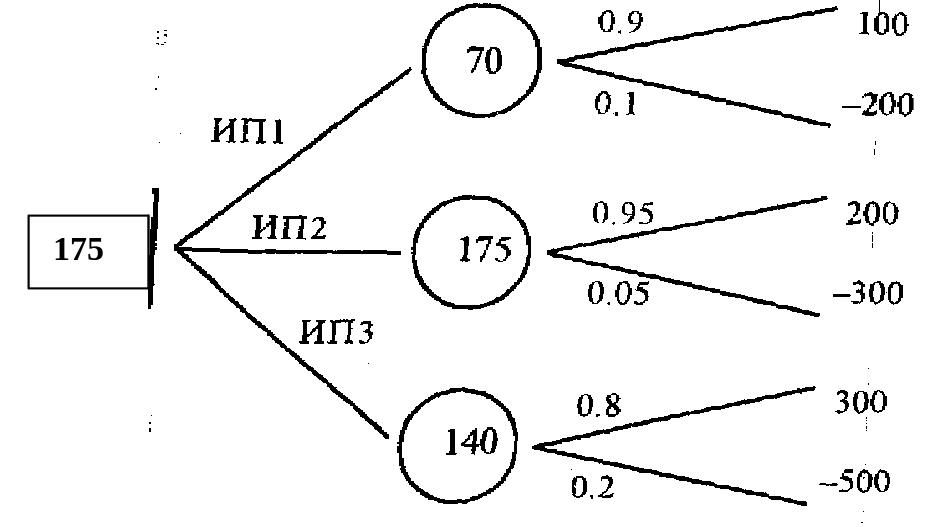
Рисунок 2 – Дерево решений
Задача 7
Добавочные вложения в расширение производства в размере Х = 50000 руб. могут увеличить прибыль от реализации продукции с Х1 = 100000 руб. до Х2 = 200000 руб., если спрос на нее вырастет. Они окажутся напрасными, если спрос не вырастет. Шансы на увеличение спроса равны Р1 = 70%.
Предположение о росте спроса обозначим как гипотезу Н1 а об отсутствии роста как Н2. Тогда Р(Н1) = 0,7 и Р(Н2) = 0,3.
За Х3 = 5000 руб. можно заказать прогноз рыночной ситуации. Эти прогнозы сбываются с вероятностью Р2 = 90%
Обозначим через А получение положительного
прогноза, а через
![]() - отрицательного. Тогда вероятность
того, что положительный или отрицательный
прогноз сбудется будет иметь вид:
- отрицательного. Тогда вероятность
того, что положительный или отрицательный
прогноз сбудется будет иметь вид:
Р(А/Н1) = Р( /Н2) = 0.9.
Вероятности того, что прогнозы окажутся ошибочными, в этом случае надо будет обозначить как
Р(А/Н2) = Р( /Н1) = 0,1.
Необходимо принять решения о целесообразности дополнительных вложений и о целесообразности заказа прогноза с целью снижения риска из-за неопределенности перспектив спроса на продукцию.
Рекомендации по решению
Проделаем вначале некоторые расчеты.
1. Определим вероятность, с которой может быть получен положительный прогноз (событие А) от специальной лаборатории, занимающейся изучением рыночной конъюнктуры. Если она окажется очень маленькой, то надо будет сразу же отказаться от заказа прогноза. Для указанной цели используем формулу полной вероятности, являющуюся по сути дела знаменателем формулы Байеса:
-
Р(А) =
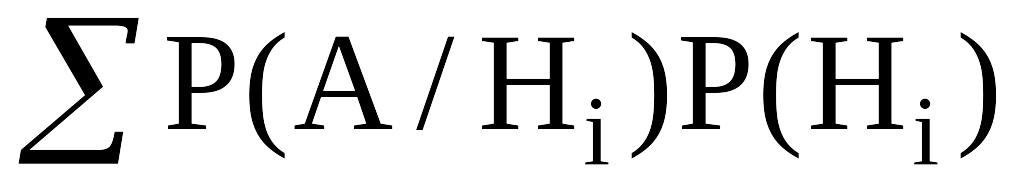 =
Р(А/Н1)Р(Н1) + P(A/Н2)P(H2)
=
Р(А/Н1)Р(Н1) + P(A/Н2)P(H2)(4)
Р (А) = 0.9 × 0.7 + 0.1 × 0.3 = 0.66.
Отсюда вероятность получения отрицательного прогноза составит:
-
Р( ) = 1 – Р(А)
(5)
Р( ) = 1 – 0.66 = 0.34.
2. Подсчитаем, с какой вероятностью можно будет ожидать рост спроса, если будет получен положительный прогноз. Для этого используем формулу Байеса:
-
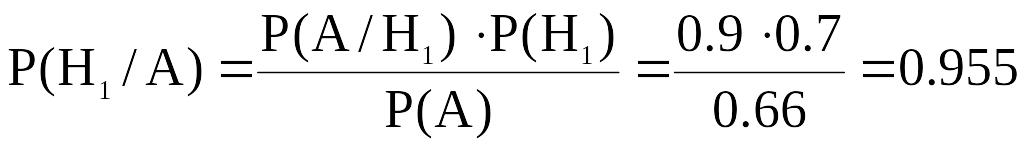
(6)
Отсюда вероятность падения спроса при получении положительного прогноза составит:
Р(Н2/А) = 1 – Р(Н1/А) = 1 – 0.955 = 0.045.
3. Вычислим, с какой вероятностью можно будет ожидать рост спроса, если будет получен отрицательный прогноз. Такое вполне может произойти, ибо лаборатория, специализирующаяся на прогнозах, не гарантирует абсолютной точности. 10 % ее прогнозов не сбываются. Для расчета упомянутой вероятности употребим опять формулу Байеса:
-
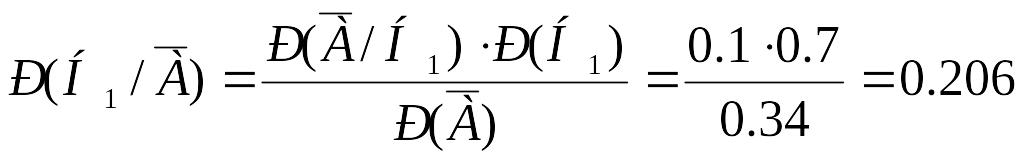
(7)
Отсюда вероятность падения спроса при получении отрицательного прогноза составит:
Р(Н2/ ) = 1 – P(Н1/ ) = 1 - 0.206 = 0.794.
Все результаты проделанных выше расчетов очень пригодятся затем при составления дерева решений, которое приведено на рисунке 3.
Оно будет иметь довольно сложную структуру.
После составления дерева решений начинаем его обратный анализ, т.е. движемся в обратном направлении: справа налево. В ходе этого находим математические ожидания выплаты для первых двух узлов неопределенности:
145 × 0.955 + 45 × 0.045 = 140.5,
150 × 0.7 + 50 × 0.3 = 120.0.
Математические ожидания проставляются в кружки, изображающие узлы неопределенности. Мы опустили расчет математического ожидания для случая получения отрицательного прогноза, получив который, надо просто отказаться от вложения средств в расширение производства.
В ходе дальнейшего движения влево нам встречаются три пункта принятия решений (квадраты). Для них выплаты максимизируются. Например, для самого верхнего квадрата мы выбираем наибольшую из величин 140.5 и 95. Она записывается в соответствующий квадрат. Аналогичным образом поступаем с двумя другими пунктами принятия решений и ставим в них числа 95 и 120. Продолжаем движение влево и встречаем еще один узел неопределенности. Подсчитываем для него математическое ожидание выплаты:
140.5 × 0.66 + 95 × 0.34 = 125.03.
Р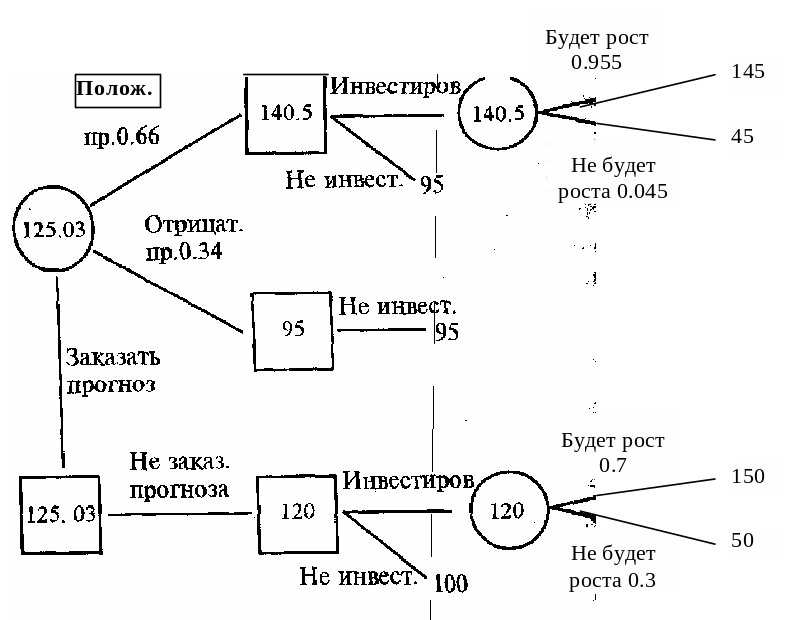 исунок
3 – Дерево решений
исунок
3 – Дерево решений
Наконец, остается последний пункт принятия решений. С него мы начинали создание дерева решений, а теперь в конце обратного анализа вновь вернулись к нему. Для него выплата максимизируется, т.е. выбирается наибольшее число из 125.03 и 120. Большим будет 125.03. Такой результат анализа предписывает нам заказать на стороне прогноз рыночной ситуации и поступать затем в соответствии с характером полученного прогноза. В данном примере стоимость прогноза, заказанного на стороне, была равна 5000 руб. При этом выплата от решения, принятого на основе прогноза, оказалась больше выплаты принятого без прогноза решения на 5030 руб. Таким образом, максимальная цена прогноза в данном случае равна 10030 руб. Купленный сверх этой цены прогноз не принесет никакой прибыли. Если бы лаборатория, составляющая прогнозы, допускала не 10, а лишь 5%-ные ошибки, максимально допустимая цена прогноза, как это можно подсчитать, выросла бы до 12500 руб. При 1%-ных ошибках она стала бы еще больше. Однако есть предел этого роста. Им является цена абсолютно точной информации. О ней уже говорилось выше. В данном примере она может быть получена на основе следующих рассуждений.
Если бы имелась абсолютно точная информация о рыночной ситуации, то, пользуясь ею, предприятие лишь тогда расширяло бы производство, когда это было бы абсолютно оправдано. Всякий риск и потери были бы полностью исключены. В таких условиях ожидаемая выплата составила бы 150000 × 0.7 + 100000 × 0.3 = 135000 руб. Не имея такой информации и не заказывая прогноза, можно получить лишь 120000 руб. Значит цена идеально точной информации равна в данном примере 135000 – 120000 = 15000. Дороже этого нельзя платить ни за какую реальную информацию, ибо никакая реальная информация не может быть идеально точной.
