Лабораторная задача QM-4

Гармонический осциллятор

Краткая теория

Стационарное решение

Потенциальная энергия многих физических систем имеет в некоторых точках пространства минимум. Разлагая в окрестности минимума потенциальную энергию в ряд, имеем

,

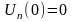где - отклонение от положения равновесия, и принимаем без ограничения общности, что . Если частица совершает малые колебания около положения равновесия, то в ряде можно ограничиться только первым членом. Частицу, совершающую гармонические колебания, называют гармоническим осциллятором.

Гармонические осцилляторы играют большую роль при иссле-довании малых колебаний систем около положения равновесия, в частности колебаний атомов в кристаллах, молекулах и т. д.

Энергия колебаний для гармонического осциллятора равна:

, (4.1)

а производная ,

и уравнение Шредингера записывается следующим образом:

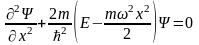. (4.2)

Для дальнейших вычислений удобно ввести следующую безразмерную величину :

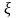. (4.3)

Обозначая производные по штрихами, имеем:

, (4.4)

где . (5)

Для определения асимптотического поведения на бесконечности заметим, что если x²>>l, в уравнении (4) можно пренебречь l по сравнению с x² и записать его в виде:

Отсюда следует, что .

Решение со знаком плюс надо отбросить, так как оно не удовлетворяет условию конечности. Волновую функцию будем искать в виде:

(6)

Для функции u после подстановки (6) в (4) получаем следующее уравнение:

. (7)

Представим функцию u в виде ряда:

(8)

Подставляя (8) в (7), имеем:

.

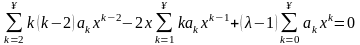Сумма бесконечного степенного ряда тождественно равна нулю только когда, когда коэффициенты при всех степенях независимой переменной равны нулю. Приравнивая нулю сумму коэффициентов при одинаковых степенях, получаем следующие рекуррентные соотношения для

определения коэффициентов a_k:

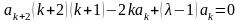. (9)

Отсюда

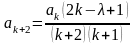. (10)

При k®¥ получаем

.

Это означает, что представляемая бесконечным рядом (8) функция растет как 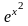. Чтобы в этом убедиться, рассмотрим разложение

в ряд:

,

или

Отсюда мы имеем:

,

что и доказывает высказанное ранее утверждение. Но чтобы функция

ψ оставалась конечной, u(ξ) не должно расти на бесконечности быстрее, чем .Чтобы удовлетворить условиям конечности ψ , ряд (8) следует ограничить n – членом, при a_n¹0 должно быть a_n+2=0. Это возможно, если

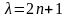. (11)

Но , тогда энергия осциллятора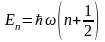 , (12) где n=0, 1, 2 ... При n=0 из формулы (12) получается, что минимальная энергия

(рис. 4.1) осциллятора равна

.

То, что минимальная энергия осциллятора не равна нулю, обусловлено специфическими квантовыми свойствами системы и связано с соотношением неопределенностей. Если бы энергия частицы была равна нулю, то частица покоилась бы и ее импульс и координата имели бы нулевые значения, что противоречит соотношению неопределенностей.

Наличие нулевой энергии осциллятора подтверждается эксперимента- ми по рассеянию света кристаллами при низких температурах. Рассеяние света связано с колебаниями атомов. С уменьшением температуры амплитуда колебаний уменьшается, стремясь, согласно классической механике, к нулю, в результате чего рассеяние должно исчезнуть. В квантовой механике при понижении температуры средняя энергия колебаний должна стремиться не к нулю, а к некоторому пределу. Именно такой ход интенсивности рассеяния света и наблюдается в экспериментах.

Волновые функции квантового осциллятора имеют вид:

, (13)

где 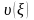- полином вида (8), ограниченный n – членом, а коэффициенты этого полинома связаны друг с другом реккурентными соотношениями (10). Учитывая эту связь, волновую функцию для уровня E_n

можно записать в виде:

(14)

где H_n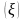 - полином Эрмита, а C_n – нормировочная константа.

Общее выражение для полиномов Эрмита имеет вид:

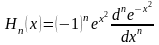, (15)

а несколько первых полиномов соответственно равны:

H₀(ξ) = 1,

H₁(ξ) = 2ξ,

H₂(ξ) = 4ξ² – 2.

Нормировочные коэффициенты C_n находятся из условия:

. (16)

Проведя интегрирование, получим:

(17)

где a² = ћ ∕ mω.

Подставляя (17) в (14), получим выражение для волновой

функции стационарных состояний осциллятора:

(18)

так как .

Волновая функция основного стационарного состояния (при n=0) кван-

тового осциллятора есть:

. (19)

В этом состоянии средние значения координаты и импульса равны нулю,

а соотношение неопределенностей 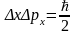дает разброс значений

p и x относительно средних величин. При этом полная энергия осцилля-

тора принимает определенное значение, равное .

Нестационарное уравнение Шредингера.

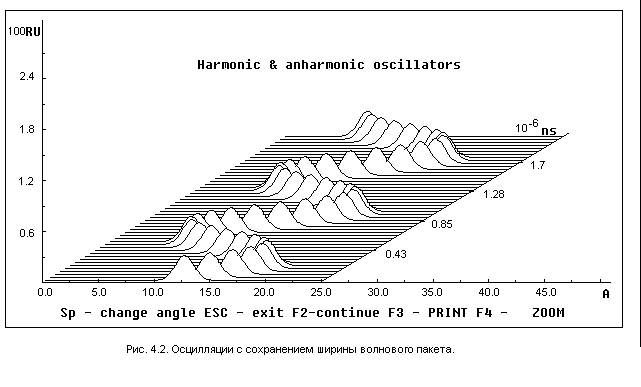
Перейдем теперь к изучению гармонического осциллятора на основе нестационарного уравнения Шредингера. С квантомеханической точки зрения для того, чтобы проследить движение частицы в гармоническом поле, мы должны решить уравнение Шредингера:

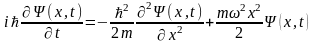(20)

Выберем волновую функцию начального состояния в виде гауссового пакета:

. (21)

Такая волновая функция соответствует частице, локализованной вблизи точки x=0 и имеющей импульс p₀. Пусть также ширина пакета . Решение задачи (20) ищется в виде разложения по собственным функциям (18) в виде:

. (22)

Коэффициенты разложения B_n и есть амплитуды вероятности обнару-

жить осциллятор в состоянии n. В результате вычислений получим для

вероятности обнаружить осциллятор в состоянии n :

|B_n|² = , (23) где = 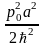- среднее число квантов в начальном состоянии.

Так как энергия начального состояния равна

, (24)

а величина , получим: Ē= ħω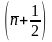 . (25) Поскольку среднее число квантов от времени не зависит, в процессе эволюции начального состояния его средняя энергия не изменяется , не изменяется и распределение вероятностей обнаружить частицу в том или ином состоянии осциллятора. Такие нестационарные состояния называются когерентными. Подставив B_n в (22), можно определить волновую функцию когерентного состояния. Плотность вероятности обнаружить частицу в различных точках пространства равна :

, (26)

и, как видно, соответствует осциллирующему гауссовому пакету с неизменной шириной a.Определение средних значений координаты и импульса частицы приводит нас к выражениям

,

, (25)

совпадающим с классическими зависимостями координаты и импульса частицы во времени. Таким образом, “в среднем” квантовая частица опять движется по классическим законам. При этом, если ширина распределения

a мала по сравнению с амплитудой колебаний x₀, то движение квантового осциллятора практически неотличимо от движения осциллятора классического.

Поскольку пакет гауссовой формы обладает минимальным произведением неопределенностей импульса и координаты, то рассматриваемый нами случай наиболее близок к классическому. Следует отметить, что сохранение формы пакета возможно только в том случае, если . В противном случае ширина пакета будет меняться во времени с частотой 2w, но сам пакет будет сохранять гауссову форму и не расплываться с течением времени. Последнее свойство пакета есть особенность гармонического потенциала. В любом другом потенциале пакет расплывается - частица постепенно делокализуется в пространстве.

Остановимся еще на важном частном случае рассмотренной задачи. Пусть начальное значение импульса равно нулю. Тогда из решения задачи о гармоническом осцилляторе (26) получаем:

, (27)

т.е. распределение вероятности обнаружить частицу в различных точках пространства не зависит от времени. Это основное стационарное состояние,

для которого , что соответствует классической частице, находящейся в положении равновесия.

На рисунках 4.2 – 4.6 приведены решения задачи о движении квантовой частицы в гармоническом потенциале при различных параметрах начального волнового пакета. Так на рис. 4.2 приведены осцилляции пакета с шириной, совпадающей с шириной волновой функции основного состояния осциллятора , а на рис. 4.3 - осцилляции пакета, начальная ширина которого .

Особый интерес представляют осцилляции “неподвижного” пакета (p₀=0) в случае . Хотя в этом случае , состояние, представленное на рис 4.4, является нестационарным и может быть представлено в виде суперпозиции различных стационарных состояний. На рис 4.5 приведены осцилляции пакета с теми же параметрами, что и на рис 4.2, но находящегося в ангармоническом потенциале вида

.

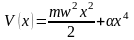Как видно, пакет не сохраняет свою форму, что соответствует делокализации частицы в пространстве.