Скорость передачи информации будет равняться
 .
.
Максимальная скорость передачи информации
называется пропускной способностью
канала связи
 .
.
Определим
пропускную способность канала связи,
когда помехи воздействуют на передаваемый
сигнал по нормальному закону. Такие
помехи обладают наибольшей эффективностью.
Энтропия шума для одного отсчетного
значения равна
 ,
где σ2
дисперсия шума. Так как элементы
независимы, то энтропия объединения
для помехи равна сумме энтропии
,
где σ2
дисперсия шума. Так как элементы
независимы, то энтропия объединения
для помехи равна сумме энтропии
 .
.
Если желательно передать наибольшее
количество информации, то надо, чтобы
энтропия объединения принятых сообщений
была максимальной. Для этого необходимо,
что бы отсчеты принимаемого сигнала
были статистически независимы и чтобы
отсчетные значения были распределены
по нормальному закону. В этом случае
энтропия принимаемых сигналов будет
равна
 .
.
Тогда
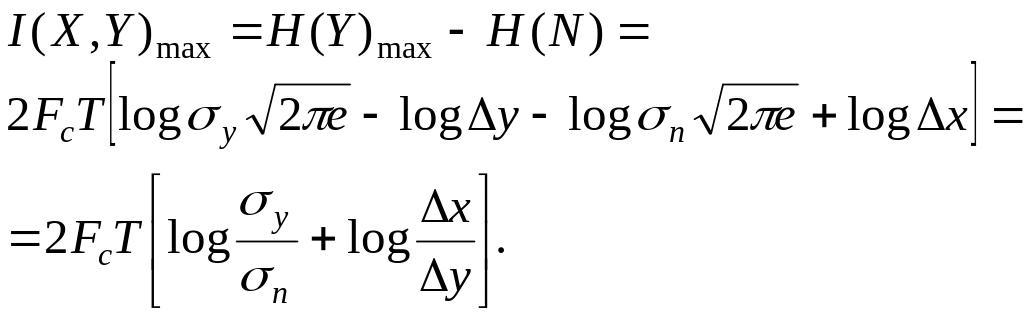
Если
точность квантования Δx
и Δy
равны, то
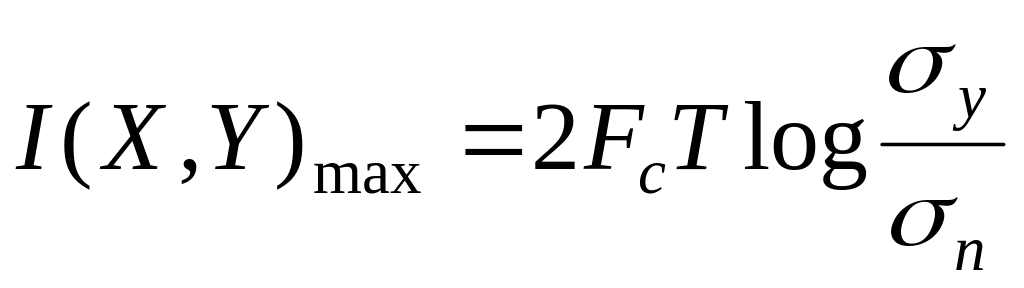 .
Дисперсия принятых сообщений определяется
как сумма
.
Дисперсия принятых сообщений определяется
как сумма
 .
Тогда
.
Тогда
 .
.
Отношение
дисперсии заменим отношением мощностей:
 .
.
Тогда
получаем следующее выражение:
 ,
,
где
P
мощность сигнала, а N
мощность помехи. Таким
образом, для увеличения I(X,
Y)max
необходимо увеличить Fс,
T
и
 .
.
Величину
 называют
«объемом сигнала». При сохранении объема
сигнала можно передать одно и то же
количество информации, используя
различные Fс,
T
и
.
называют
«объемом сигнала». При сохранении объема
сигнала можно передать одно и то же
количество информации, используя
различные Fс,
T
и
.
С
учетом сказанного определим пропускную
способность непрерывного канала связи:
 .
.
Эта
формула указывает, что наибольшая
скорость передачи информации прямо
пропорциональна полосе частот и
соотношению между мощностью сигнала и
мощностью помехи.
В заключение отметим, что для непрерывных
каналов связи также справедливы теоремы
Шеннона о кодировании (предполагается,
что кодируются выборки непрерывного
сигнала, взятые с интервалом дискретизации,
величина которого не больше значения
определяемого теоремой Котельникова).
41


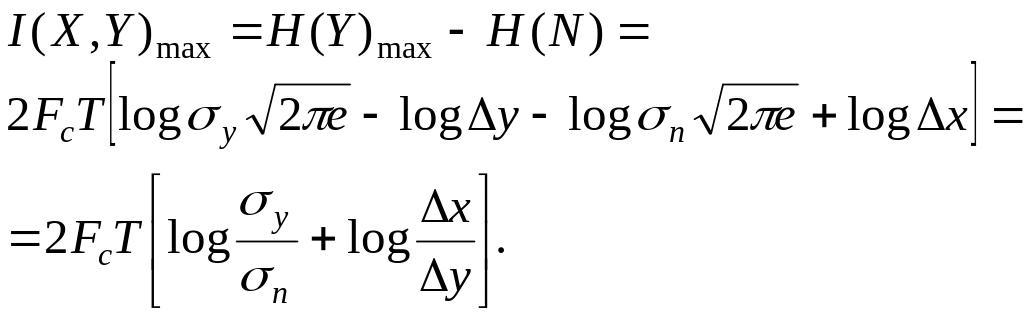
 .
. .
.