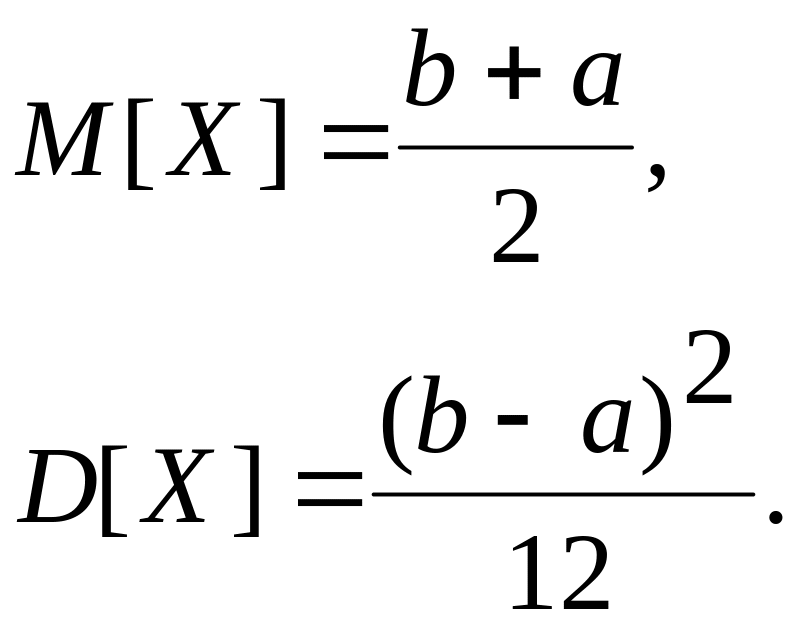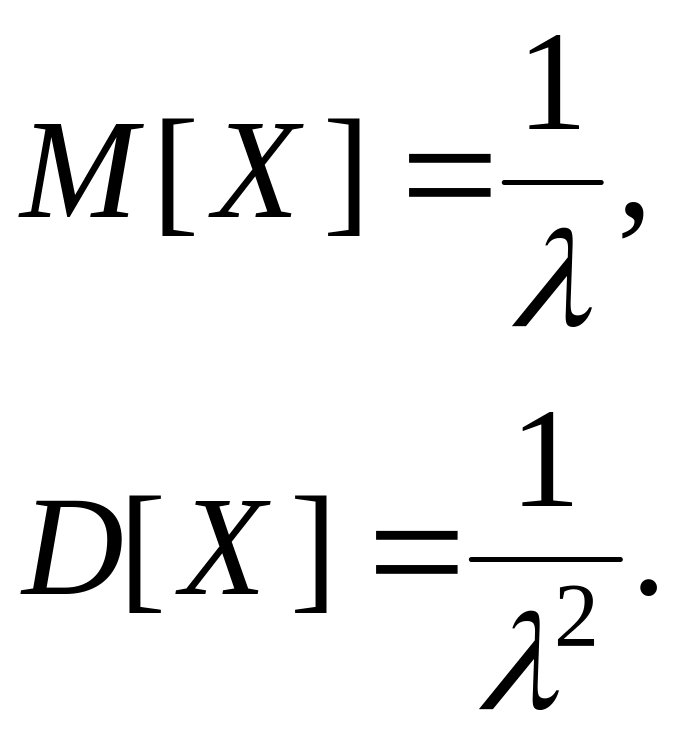2.5. Законы распределения непрерывных случайных величин
Рассмотрим
несколько распространенных законов
распределения случайных величин.
1.
Равномерное
распределение.
Непрерывная случайная величина называется
равномерно распределенной на интервале
[a,
b],
если плотность ее распределения имеет
постоянное значение. Математическое
ожидание и дисперсия равномерно
распределенной случайной величины
равны:
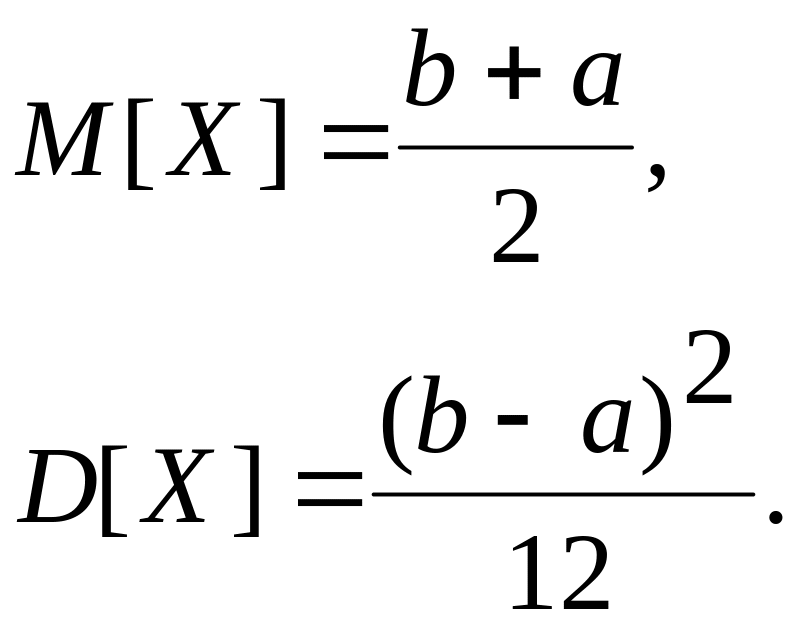
2.
Показательное
распределение.
Показательным
(экспоненциальным) распределением
случайной величины называют распределение
случайной величины, которое описывается
плотностью распределения
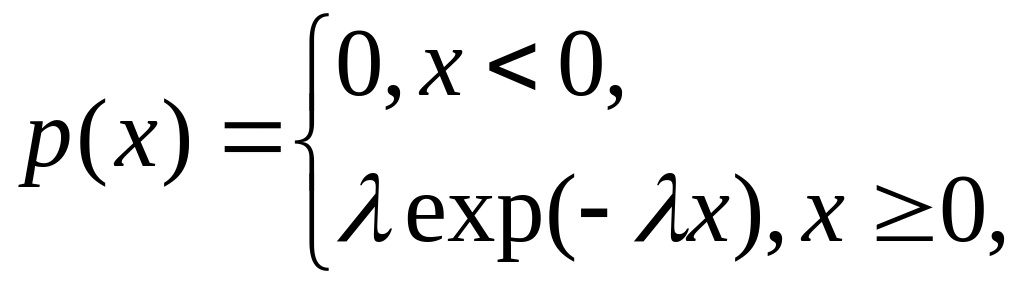
где
– положительная постоянная величина.
Математическое ожидание и дисперсия в
этом случае определяются по формулам
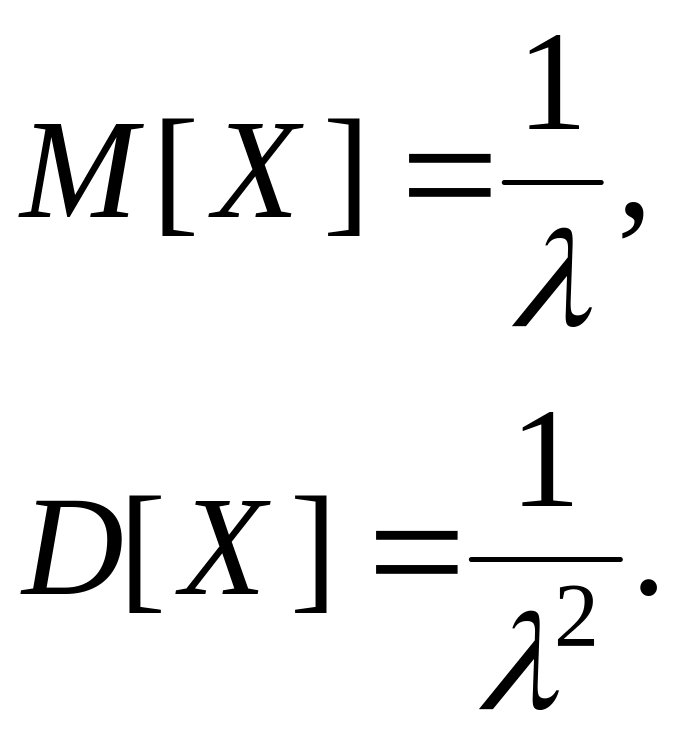
3.
Нормальное
распределение.
Нормальный закон распределения (закон
Гаусса), наиболее часто встречающийся
на практике закон распределения. На его
основе описывают случайные возмущения
и отклонения основных характеристик
процессов и систем, ошибки измерений и
т.д. Этот закон является предельным
законом, к которому приближаются другие
законы распределения при весьма часто
встречающихся типичных условиях.
Непрерывная случайная величина называется
распределенной по нормальному закону,
если ее плотность вероятности определяется
выражением:
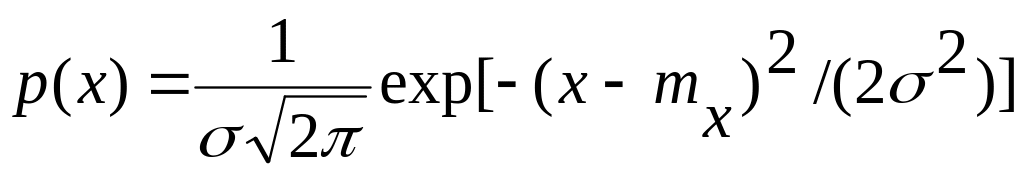 ,
,
где
параметры mx
и
называются параметрами распределения
и представляют собой математическое
ожидание и среднеквадратическое
отклонение соответственно.
15