2. Элементы теории вероятностей

2.1. Основные понятия и определения теории вероятностей

Многие положения теории информации базируются на математическом аппарате теории вероятностей, которая изучает закономерности случайных явлений, т.е. таких явлений которые при многократном повторении в одних и тех же условиях протекают каждый раз несколько по иному.

Основными понятиями теории вероятностей являются понятия события и вероятности события. Событие – это всякий факт, который может произойти или не произойти в результате некоторого эксперимента. Различают достоверные, невозможные и случайные события. Достоверным событием называют событие, которое обязательно произойдет в результате эксперимента. Невозможным событием называют событие, которое заведомо не произойдет в результате эксперимента. Случайным событием называют событие, которое может либо произойти, либо не произойти в результате эксперимента.

Вероятность P(A) события A есть численная мера объективной возможности его наступления при осуществлении определенного комплекса условий эксперимента Q. Если вероятность наступления события A равна p, то это записывают в виде Р(А) = р. Вероятность имеет следующие свойства:

1) вероятность достоверного события равна единице;

2) вероятность невозможного события равна нулю;

3) вероятность случайного события А есть положительное число из интервала от 0 до 1.

Оценить значение вероятности события A можно с помощью относительной частоты

(А) = m / n,

где n – число независимых испытаний, m – число испытаний, в которых появилось событие А.

2.2. Основные теоремы теории вероятностей

Теорема 2.1. Сложение вероятностей несовместных событий. Вероятность суммы несовместных событий, т.е. событий, из которых в результате эксперимента может произойти только одно, равна сумме их вероятностей:

.

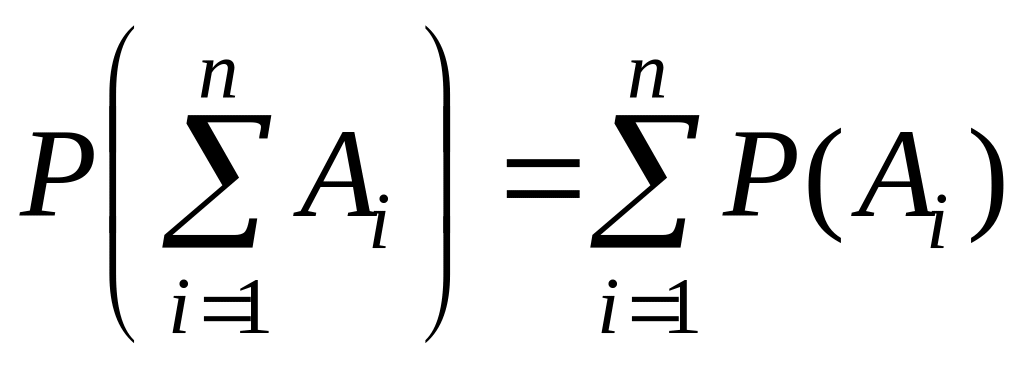Если события А₁, А₂, …, А_n образуют полную группу несовместных событий, т.е. в результате эксперимента одно из событий должно произойти, то сумма их вероятностей равна 1:

.

В частности сумма вероятностей двух противоположных событий равна 1:

Р(А) + Р( ) = 1.

Теорема 2.2. Сложение вероятностей совместных событий. Вероятность суммы совместных (произвольных) событий определяется через вероятность произведений этих событий, взятых по одному, по два, по три и т.д. по формуле:

.

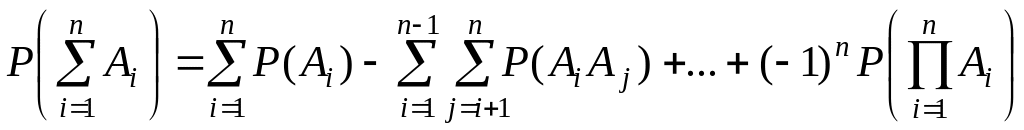При этом имеет место неравенство:

Р(А₁ + А₂ + … + А_n)  Р(А₁) + Р(А₂) +…+ Р(А_n).

Теорема 2.3. Произведение произвольного числа событий. Вероятность произведения произвольного числа событий определяется через вероятности суммы этих событий, взятых по одному, по два, по три и т.д. по формуле

.

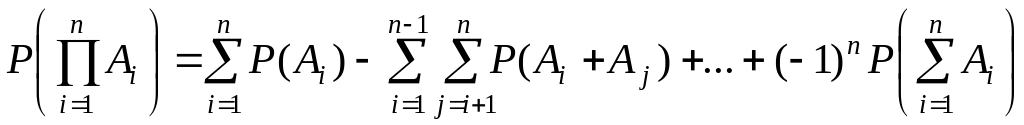Вероятность события А, вычисленная при условии, что имело место событие В, называется условной вероятностью события А и обозначается Р(А | В). Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет:

Р(А | В) = Р(А).

И обратно, событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет:

Р(А | В)  Р(А).

Теорема 2.4. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

Р(АВ) = Р(А)Р(В | А).

Если событие А не зависит от события В, то и событие В не зависит от события А. Вероятность произведения двух независимых событий A и B равна произведению вероятностей этих событий:

Р(АВ) = Р(А)Р(В).

Теорема 2.5. Вероятность произведения независимых событий равна произведению вероятностей этих событий:

Р(А₁, А₂, …, А_n) = P(А₁)P(А₂)…P(А_n).

Следствием теорем сложения и умножения вероятностей является формула полной вероятности:

,

где A – произвольное случайное событие, Н₁, Н₂, …, Н_n – несовместные события, образующие полную группу (гипотезы).

Теорема 2.6. Теорема гипотез (формула Байеса). Пусть Н₁, Н₂, …, Н_n – полная группа несовместных событий. Тогда, если произошло событие А, то

имеет место равенство

.
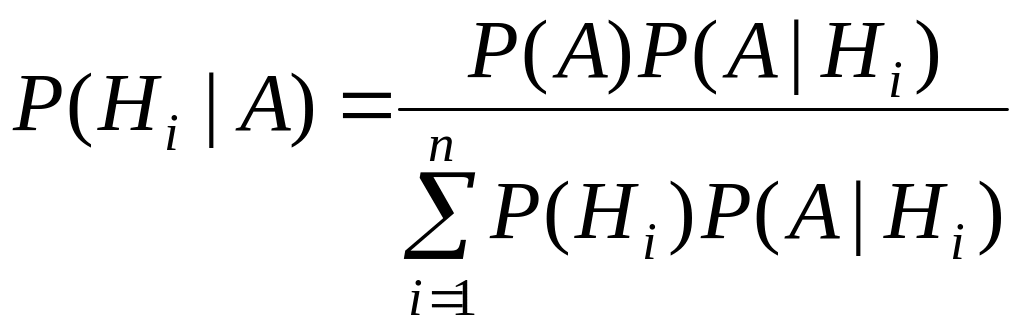