17

Содержание

Введение……………………………………………………………………………...3

Часть 1: Сплайны…………………………………………………………………….4

1.1 Определение сплайн-функции…………………………………………………..4

1.2 Кубические сплайны…………………………………………………………….4

1.3 Фундаментальные сплайны……………………………………………………..5

Часть 2: Дифференциальные уравнения…………………….……………………...7

2.1. Решение дифференциальных уравнений второго порядка с помощью кубических сплайнов. Метод сплайн-коллокации………………………………...7

2.2 Решение задачи методом сплайн-коллокации…………………………………9

Часть 3: Задача Коши́………………………………………………………………11

3.1. Определение…………………………………………………………………....11

3.2 Решение задачи Коши методом дифференциального исчисления………….12

Заключение…………………………………………………………………………14

Список используемой Литературы………………………………………………..15

Приложение………………………………………………………………………...16

Введение

Сплайн – функция – это новая быстрая развивающаяся область теории приближения функции и численного анализа. Получив распространение в 60 – ч годах, главным образом как средство интерполяции сложных кривых, сплайн в дальнейшем стали важным методом для решения разнообразных задач вычислительной математики и прикладной геометрии. Крупный вклад в развитие теории сплайн-функций и её приложений внесли сибирские ученые.

По сравнению с классическим аппаратом приближения многочленами сплайн – функции обладают по крайне мере двумя важными преимуществами. Во - первых, бесспорно лучшими аппроксимативными свойствами. Во - вторых, удобством реализации построенных на их основе алгоритмов, на ЭВМ.

Бурное развитее теории сплайн - функции одной переменной как аппарата численного анализа было обусловлено главным образом двумя причинами:

1. хорошей сходимостью сплайнов к аппроксимируемым объектам.

2. Простой в реализации алгоритмов построения сплайнов на ЭВМ.

Курсовая разделена на три части и приложение.

В первой части дано определение: сплайна, кубического сплайна и построены фундаментальные сплайны на отрезке 0, 1 с шагом 0.5.

Во второй части рассмотрено дифференциальное уравнение второго порядка и решение его методом сплайн – коллокации.

В третей части решена задача Каши для дифференциального уравнения второго порядка.

Приложение содержит таблицы фундаментальных сплайнов. К курсовой работе прилагается программа для решение задачи Коши.

Часть 1: Сплайны

1. Определение сплайн-функции

Сплайн – функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом.

Максимальная степень из использованных полиномов называется сплайн. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.

Сплайны имеют многочисленные применения как в математической теории, так и а разнообразных вычислительных приложениях. В частности сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.

2. Кубические сплайны

Некоторая функция f(x) задана на отрезке  , разбитом на части  ,  . Кубическим сплайном дефекта 1 называется функция , которая:

• на каждом отрезке   является многочленом степени не выше третьей;

• имеет непрерывные первую и вторую производные на всём отрезке  ;

• в точках 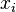  выполняется равенство 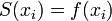 , т. е. сплайн   интерполирует функцию f в точках  .

Для однозначного задания сплайна перечисленных условий недостаточно, для построения сплайна необходимо наложить какие-то дополнительные требования.

Естественным кубическим сплайном называется кубический сплайн, удовлетворяющий также граничным условиям вида:

Теорема: Для любой функции   и любого разбиения отрезка   существует ровно один естественный сплайн S(x), удовлетворяющий перечисленным выше условиям.