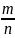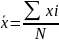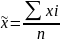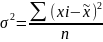26,032,13 лекция

Для изучения влияния какого-либо фактора на результат необходимо оценить вариацию признака, которая вызвана вариацией фактора. В аналитической группировке эту задачу решают на основе межгрупповой дисперсии. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группированного признака фактора на результативный признак. Показателями тесноты связи служит коэффициент детерминации и эмпирическое корреляционное отношение. Коэффициент детерминации определяет как долю межгрупповой дисперсии в общей дисперсии. 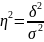, -этта

Эмпирический коэффициент детерминации показывает долю вариации результативного признака под влиянием факторного признака(остальная часть общей вариации результативного признака обусловлена влиянием прочих факторов)

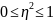
Если связь отсутствует то этта квадрат равно 0

Если связь между признаками функциональная, то этта квадрат равно 1

Например: 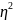= 0,7 показывает что на 70% вариация признака (у) обусловлена вариацией факторного признака (х) и на 30% прочими факторами.

Эмпирическое корреляционное отношение это корень квадратный из коэффициента детерминации 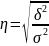так же используется для оценки тесноты связи между группировочным признаком (х) и результативным признаком (у)

Шкала Чэддока

Эта связь

0 – отсутствует

0 – 0,2 очень слабая

0,2 - 0,3 – слабая

0,3 – 0,5 – умеренная

0,5 – 0,7 – заметная

0,7 – 0,9 – тесная

0.9 – 0,99 – весьма тесная

1 - функциональная

Тема 6. Выборочное наблюдение.

1. Способы отбора и виды выборочного наблюдения.

2. Ошибки выборки

3. Задачи, решаемые при применении выборочного наблюдения

1. Способы отборы и виды выборочного наблюдения

Выборочное наблюдение – это вид не сплошного наблюдения, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке. Отобранная часть изучается, а результат распространяется на всю исходную совокупность.

Генеральная совокупность – это совокупность, из которой производится отбор.

Выборочная совокупность (выборка) – часть единиц генеральной совокупности, которая непосредственно обследуется при выборочном наблюдении.

Таблица 1 – Основные характеристики генеральной и выборочной совокупности

Характеристика	Генеральная совокупность	Выборочная совокупность
Объем совокупности	N	N
Число единиц совокупности обладающих обследуемым признаком	M	m
Доля единиц обладающих обследуемым признаком	P=	W=
Среднее значение признака
Дисперсия количественного признака	Генеральная дисперсия	Выборочная дисперсия
Дисперсия альтернативного признака (доли)
Число серий	R	r

Основная задача выборочного наблюдения на основе характеристик выборки получить достоверное суждение о показателях (характеристиках) генеральной совокупности

Принципы выборочного наблюдения.

1. Принцип случайного отбора, т. е у отдельных единиц генеральной совокупности должна быть равная возможность попасть в выборочную совокупность.

2. Принцип достаточного числа единиц выборки.

Соблюдение этих принципов позволяет получить репрезентативную выборку. Отбор единиц в выборку может быть повторным и безповторным. При повторном отборе единица генеральной совокупности, попавшая в выборку после обследования, возвращается в генеральную совокупность и в дальнейшем отборе участвует. При безповторном отборе единица генеральной совокупности, попавшая в выборку, после обследования не возвращается в генеральную совокупность и в дальнейшем отборе не участвует.

Виды выборок.

1. Собственно-случайная. Отбор производится из всей массы единиц генеральной совокупности без предварительного разделения на группы. При этом единицы отбираются в случайном порядке, не зависящем ни от расположения единиц в совокупности, ни от значения признака.(жеребьевка, таблица случайных чисел)

2. Механическая . Применяется в тех случаях когда генеральная совокупность каким–либо образом упорядочена. (номера домов). При проведении механического отбора устанавливают шаг отсчета (h) т.е. расстояние между отбираемыми единицами. h = N/n. И начала отсчета – номер единицы которая должна быть обследована первой. Механический отбор всегда бесповторный при достаточно большом объеме совокупности механический отбор по точности близок к собственно-случайной выборки.

3. Типическая. Используется в тех случаях, когда все единицы генеральной совокупности могут быть объединены в несколько крупных типических групп по какому–либо существенному признаку. Отбор единиц в выборку осуществляется собственно – случайным или механическим способом. Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп , либо пропорционально внутригрупповой вариации признака.

4. Серийная. Заключается в собственно – случайном или механическом отборе групп единиц(серий) внутри которых производится сплошное наблюдение. Единицей отбора является группа или серия, а не отдельные единицы генеральной совокупности.

5. Комбинированная. Предполагает использование нескольких рассмотренных выше способов выборки.