Вариант 4
1. Дан ряд распределения ДСВ :
-
X
0
1,5
3
3,5
p
0,2
0,4
0,3
0,1
Найти:
функцию распределения СВ X и построить ее график;
математическое ожидание, дисперсию, среднее квадратическое отклонение;
.
Построить закон распределения случайной
величины
.
Найти математическое ожидание
и дисперсию
двумя способами.
2. Записать закон распределения дискретной случайной величины X. Составить функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
В группе спортсменов 4 лыжника и 8 конькобежцев. Из нее случайным образом отобрано 4 спортсмена. СВ X – число лыжников среди отобранных спортсменов.
3. Дана плотность распределения p(x) СВ X. Найти константу C. Найти функцию распределения F(x). Найти вероятность попадания СВ X на отрезок [a; b]. Найти математическое ожидание и дисперсию.
,
.
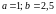4. Длительность времени безотказной работы каждого из четырех модулей технологической системы имеет показательное распределение. Среднее время безотказной работы для каждого модуля равно 1200 ч. Технологическая система работает при условии безотказной работы хотя бы трех модулей. Определить вероятность безотказной работы технологической системы в течение не менее 1700 ч, если время безотказной работы каждого модуля не зависит от времени работы других модулей.
5. На станке изготовляются втулки. Длина втулки представляет собой случайную величину, распределенную по нормальному закону. Среднее значение длины втулки равно 25 см и дисперсия равна 0,09 см2. Найти вероятность того, что длина втулки заключена между 23 и 27,3 см.
6. Закон распределения системы св (X, y) имеет вид:
Y X |
3 |
1 |
6 |
1,4 |
0,14 |
p21 |
0,35 |
2,8 |
0,05 |
0,22 |
0,13 |
Найти:
значение вероятности p21;
законы распределения составляющих (маргинальные распределения компонент);
условный закон распределения составляющей X при условии, что составляющая Y=1,4;
математическое ожидание, дисперсию и среднее квадратическое отклонение для каждой из СВ X и Y;
условное математическое ожидание M(X/Y=1,4);
корреляционный момент KXY; коэффициент корреляции между X и Y.
Вариант 5
1. Дан ряд распределения ДСВ :
-
X
1,5
2,5
4
5,5
p
0,2
0,3
0,4
0,1
Найти:
функцию распределения СВ X и построить ее график;
математическое ожидание, дисперсию, среднее квадратическое отклонение;
.
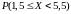Построить закон распределения случайной величины . Найти математическое ожидание и дисперсию двумя способами.
2. Записать закон распределения дискретной случайной величины X. Составить функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Вероятность поражения цели при одном выстреле равна 0,7. СВ X – число поражений цели при пяти выстрелах.
3. Дана плотность распределения p(x) СВ X. Найти константу C. Найти функцию распределения F(x). Найти вероятность попадания СВ X на отрезок [a; b]. Найти математическое ожидание и дисперсию.
,
.
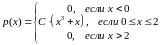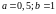4. Длительность времени безотказной работы каждого из пяти модулей технологической системы имеет показательное распределение. Среднее время безотказной работы для каждого модуля равно 800 ч. Технологическая система работает при условии безотказной работы хотя бы четырех модулей. Определить вероятность безотказной работы технологической системы в течение не менее 1500 ч, если время безотказной работы каждого модуля не зависит от времени работы других модулей.
5. Случайная величина распределена по нормальному закону. Математическое ожидание и дисперсия этой величины соответственно равны 9 и 16. Найти вероятность того, что отклонение величины от ее математического ожидания по модулю не превзойдет 5.