Вариант 1

1. Дан ряд распределения ДСВ :

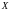X	2	-1	0	6
p	0,2	0,3	0,4	0,1

Найти:

1. функцию распределения СВ X и построить ее график;

2. математическое ожидание, дисперсию, среднее квадратическое отклонение;

3. .

Построить закон распределения случайной величины 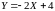. Найти математическое ожидание 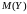и дисперсию двумя способами.

2. Записать закон распределения дискретной случайной величины X. Составить функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

В партии из 25 изделий 6 бракованных. Для контроля их качества случайным образом отбирают пять изделий. СВ X – число бракованных изделий среди отобранных

3. Дана плотность распределения p(x) СВ X. Найти константу C. Найти функцию распределения F(x). Найти вероятность попадания СВ X на отрезок [a; b]. Найти математическое ожидание и дисперсию.

, .

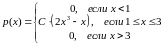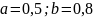4. Длительность времени безотказной работы каждого из четырех модулей технологической системы имеет показательное распределение. Среднее время безотказной работы для каждого модуля равно 700 ч. Технологическая система работает при условии безотказной работы хотя бы четырех модулей. Определить вероятность безотказной работы технологической системы в течение не менее 1200 ч, если время безотказной работы каждого модуля не зависит от времени работы других модулей.

5. При изготовлении некоторого изделия его вес подвержен случайным колебаниям. Стандартный вес изделия равен 30 г, его среднее квадратическое отклонение равно 0,7, а вес подчинен нормальному закону. Найти вероятность того, что вес наугад выбранного изделия находится в пределах от 25 до 32 г.

6. Закон распределения системы СВ (X, Y) имеет вид:

Y X	 3	1	3
 0,7	0,14	0,31	0,09
3,3	p12	0,20	0,08

Найти:

1. значение вероятности p₁₂;

2. законы распределения составляющих (маргинальные распределения компонент);

3. условный закон распределения составляющей X при условии, что составляющая Y=3,3;

4. математическое ожидание, дисперсию и среднее квадратическое отклонение для каждой из СВ X и Y;

5. условное математическое ожидание M(X/Y=3,3);

6. корреляционный момент K_XY; коэффициент корреляции между X и Y.

Вариант 2

1. Дан ряд распределения ДСВ :

X	1,5	0,5	1	3
p	0,2	0,4	0,3	0,1

Найти:

1. функцию распределения СВ X и построить ее график;

2. математическое ожидание, дисперсию, среднее квадратическое отклонение;

3. .

Построить закон распределения случайной величины . Найти математическое ожидание и дисперсию двумя способами.

2. Записать закон распределения дискретной случайной величины X. Составить функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

Для стрелка вероятность попасть в «яблочко» при одном выстреле равна 0,25. Спортсмен сделал шесть выстрелов. СВ X – число попаданий в «яблочко».

3. Дана плотность распределения p(x) СВ X. Найти константу C. Найти функцию распределения F(x). Найти вероятность попадания СВ X на отрезок [a; b]. Найти математическое ожидание и дисперсию.

, .

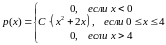4. Длительность времени безотказной работы каждого из пяти модулей технологической системы имеет показательное распределение. Среднее время безотказной работы для каждого модуля равно 800 ч. Технологическая система работает при условии безотказной работы хотя бы трех модулей. Определить вероятность безотказной работы технологической системы в течение не менее 1200 ч, если время безотказной работы каждого модуля не зависит от времени работы других модулей.

5. Значение веса пойманной рыбы подчиняется нормальному распределению с параметрами a=325г, =49г. Найти вероятность того, что вес одной рыбы будет от 300 до 370 г.