Аэростатические и газостатические опоры скольжения

В зазор между шпинделем и подшипником подается сжатый воздух.

ДОСТОИНСТВА:

1. Экологическая чистота;

2. малое тепловыделение из-за малой вязкости воздуха;

3. простая система подачи воздуха под давлением;

4. высокая долговечность.

НЕДОСТАТКИ:

1. Низкая нагруженная способность.

Применяются в небольших высокоскоростных прицинзионных станках с частотой вращения до 300…500 тыс. оборотов в минуту.

Такие опоры могут быть радиальными:

И упорными:

КРИТЕРИЙ РАСЧЕТА

• На статическую жесткость

• На нагруженную способность.

Электромагнитные опоры шпинделей

ДОСТОИНСТВА:

• Отсутствие потерь на трение,

• Экологическая чистота

• Большая, регулируемая по величине статическая жесткость;

• Возможность регулирования параметров подшипника.

Могут быть радиальные и упорные:

1-корпус, 2-шпиндель, 3-диск, который жестко связан со шпинделем, 4-диск, жестко связанный с корпусом, 5-обмотка.

28. Расчет шпинделей

Осуществляется по критериям: прочность, виброустойчивость, жесткость.

Расчёт на прочность: корпуса, тяжело нагруженные шпинделя.

Расчет на прочность выполняется только как проверочный.

При расчете определяется собственная частота колебаний шпинделя и сравнивается с частотой вынужденных колебаний, для исключения резонанса это расхождение должно быть до 30% - для точных расчетов, для неточных – в несколько раз.

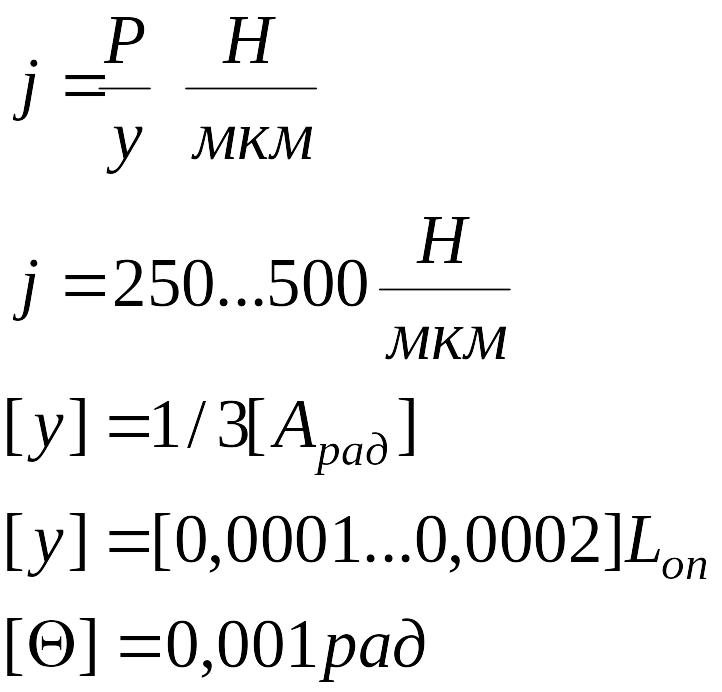
На шпиндель в общем случае действуют силы:

1. Силы резания: Рх; Ру; Рz;

2. Реакция от приводного колеса или шкива;

3. Реакция передачи, которая передает движение в другую кинематическую цепь (цепь подач токарного станка);

4. Предварительный натяг в подшипниках;

5. Сила тяжести шпинделя;

6. Силы инерции сил качения в быстрых шпинделях.

5 и 6 в большинстве случаев пренебрегают.

В общем случае шпиндель имеет пространственную нагруженность, следовательно, расчет ведется в двух взаимно перпендикулярных плоскостях, после чего осуществляется геометрическое суммирование прогибов и углов поворота.

ПРИМЕР: рассмотрим двухопорный шпиндель, на который в одной из плоскостей (УХ) действуют силы.

Р₁ – от сил резания, Р₂ – от приводного зубчатого колеса, Р₃ – от передачи, которая передает вращение в другую кинематическую цепь.

Рассмотрим случаи:

1. Шпиндель упругий, а опоры абсолютно жесткие;

2. Опоры упругие, а шпиндель абсолютно жесткий;

3. Суммарный случай 1 и 2.

Аналогичные расчеты для ZХ, затем выполняем геометрическое суммирование величины прогиба и угла поворота

Последовательность полного расчета шпинделя на жесткость

1. Выбирается расчетная схема;

2. определяем силы и моменты, которые действуют на шпиндель в 2-х плоскостях;

3. Определяем реакции опор;

4. Ступенчатый вал (шпиндель) приводится к валу постоянного сечения, который называется эквивалентным валом.

5. Определяем коэффициент приведения для каждой ступени.

6. Умножением на коэффициент приведения для каждой ступени определяются эквивалентные силы и моменты.

7. Записывается дифференциальное уравнение 2-го порядка для упругой оси шпинделя которое, например, для плоскости ХУ имеет вид:

,

где Е – модуль упругости металла шпинделя, У_{э –} момент инерции.

8. Первым интегрированием получаем:

- угол поворота в каждой точке шпинделя.(в ху)

9. Вторым интегрированием получаем величину прогиба в каждой точке шпинделя.

10. Определяем У и _ху от упругого смещения опор, для чего записываем уравнение прямой в соответствии со схемой 2:

11. Аналогичный расчет производится для плоскости ХZ.

12. Производим геометрическое суммирование по 2-м плоскостям.

13. Производим сравнение с допустимыми значениями.

При заданном значении вылета переднего конца шпинделя а, увеличение межопорного расстояния L_оп по-разному влияет на y_п(ш), y_п(оп)