2.7. Частный случай кубической формы от двух переменных
Рассмотрим
частный
случай кубической формы от двух
переменных. Пусть
имеет следующий вид
=
.
(1)
Имеем
= 0,
(2)
= 0. (3)
Из (2) находим
выражение
,
подставляя которое в (3), получаем
- 2
+
+ 12
(
= 0,
откуда получаем
2 решения: 1)
=
,
2)
= (4
-
)(12
(
,
(4
-
)(12
(
.
Итак, имеем две стационарные точки.
Являются ли полученные стационарные
точки экстремальными и максимумами или
минимумами или не являются точками
экстремума проверим в соответствии с
п. 1.2 в зависимости от конкретных исходных
данных. Матрица Гессе имеет следующий
вид
.
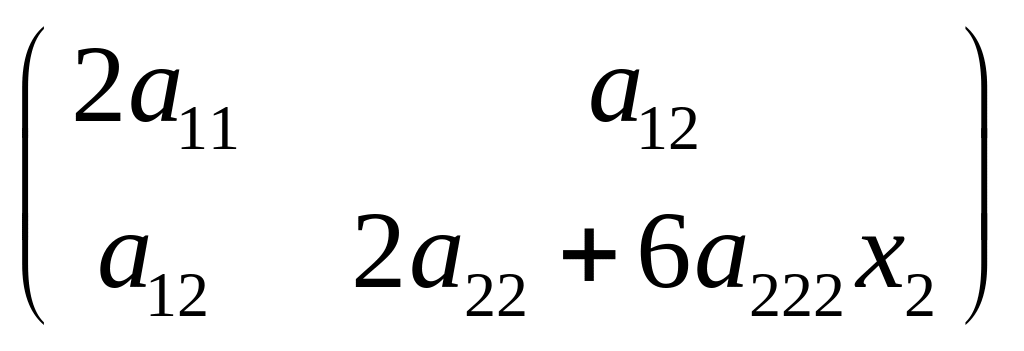1. Рассмотрим случай решения 1: = . В этом случае матрица Гессе имеет вид
.
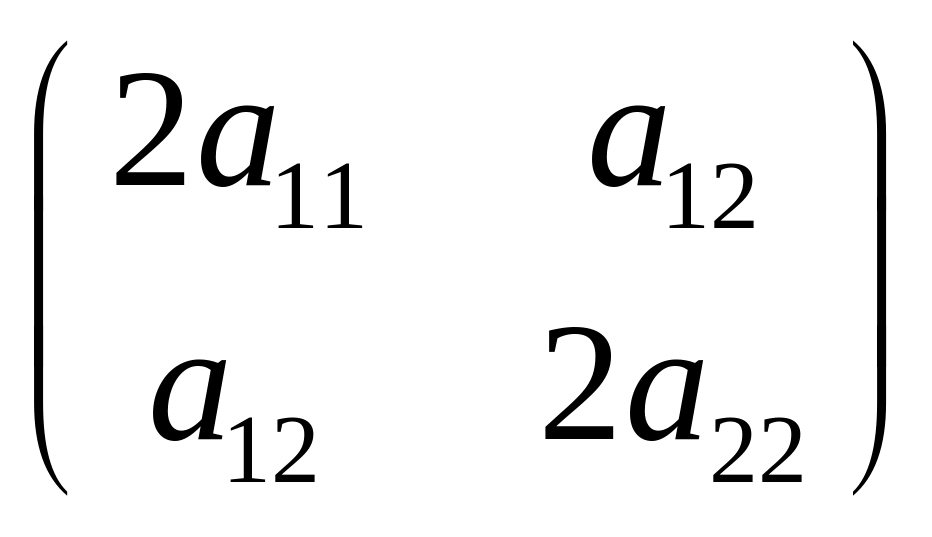Если
и
,
то у
будет минимум. Если
и
,
то у
будет максимум. Во всех других случаях
экстремума у
не будет.
2. Рассмотрим случай решения 2: = (4 - )(12 ( , (4 - )(12 ( . В этом случае матрица Гессе имеет вид
=
.
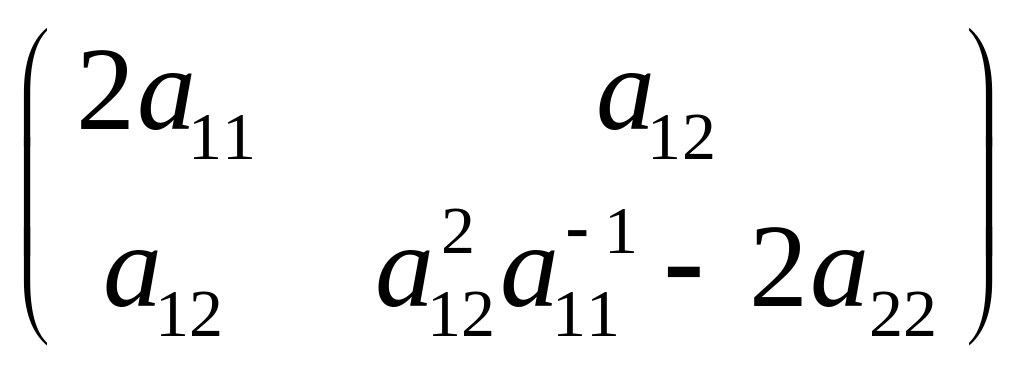Если
и
,
то у
будет минимум. Если
и
,
то у
будет максимум. Во всех других случаях
экстремума у
не будет.
Заметим, что определитель матрицы Гессе в рассматриваемых двух стационарных точках отличается только знаком.
Частный случай кубической формы от произвольного количества переменных
Рассмотрим частный случай кубической формы от произвольного
количества переменных. Пусть имеет следующий вид
=
.
(1)
Приравнивая частные производные первого порядка от нулю, получаем следующую систему уравнений
= 0,
(2)
= 0, (3)
…
= 0, (4)
…
= 0. (5)
Перейдем к решению системы уравнений (2-5). Из (2) находим выражение через . Имеем
. (6)
Подставляя (6) в (3), получаем
.
(7)
Из (4) находим
рекуррентную формулу, выражающую
через
и
,
имеющую вид
.
(8)
Из (8) следует, что
рекуррентно выражается через
и
следующей формулой
=
.
(9)
Подставляя (9) в (5), получаем уравнение для определения , а именно,
= 0.
(10)
Легко убедиться
в том, что (10) является полиномом степени
.
Находя из него значение
и последовательно подставляя его в
рекуррентные формулы (6) – (9), определяем
значения
.
Полиномиальное уравнение относительно (10) имеет корней, которые находятся известными методами. Исключая из них комплексные корни, получаем действительных корней. Тогда имеем наборов решений ( , ). Определение того, какой из этих наборов дает минимум или максимумом целевой функции или не является экстремумом в зависимости от конкретных исходных данных, можно произвести непосредственно перебором или в соответствии с п. 2.2.
Оптимальные задачи, как отмечалось выше, не всегда имеют решение. Приведем пример такой задачи.